Fisica

Costanti Fisiche

Unità Misura

Esercizi Fisica

Applet Java

Quesiti

Moto armonico                                     

Esercizio n. 1

Una massa m = 200 g oscilla orizzontalmente, in assenza di attrito, all’estremità di una molla orizzontale, per la quale k = 7,0 N/m.

Se la massa viene spostata 5,0 cm dalla posizione di equilibrio e poi rilasciata, si calcoli:

a)  La sua velocità massima.

b)  La sua velocità quando si trova a 3,0 cm dalla posizione di equilibrio.

c)  La sua accelerazione in entrambi i casi considerati.

R.: 0,2959 m/s ;  0,237 m/s ; 0 ; 1,05 m/s² ;

Esercizio n. 2

Una massa m = 50 g oscilla con moto armonico semplice, in assenza di attrito, all’estremità di una molla orizzontale.

Se l’ampiezza del moto è x_o = 12 cm ed il periodo è T = 1,70 s, si determini:

a)  La costante elastica.

b)  La velocità massima della massa.

c)  La sua accelerazione massima.

d)  La velocità quando lo spostamento è 6,0 cm.

e)  La sua accelerazione quando x = 6 cm.

R.: 0,68 N/m ;  0,44 m/s ; 1,6 m/s² ; 0,38 m/s ; 0,82 m/s² ;

Esercizio n. 3

Una massa m₁ = 50 g è appesa all’estremità di una molla che rispetta la legge di Hooke.

Quando alla molla viene aggiunta la massa m₂ = 20 g, essa subisce un ulteriore allungamento di 7,0 cm. Si determini:

a)  La costante elastica.

b)  Se la massa m₂ viene rimossa, quale sarà il periodo del moto.

R.: 2,8 N/m ;  0,84 s ;

Esercizio n. 4

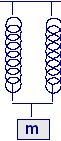
A due molle identiche, per le quali k = 20 N/m, viene attaccata una massa m = 0,30 kg, come in figura.

Si calcoli il periodo del moto di tale sistema, trascurando le forze d’attrito.

R.: 0,54 s ;  

Esercizio n. 5

A due molle identiche, per le quali k = 20 N/m, viene attaccata una massa m = 0,30 kg, come in figura.

Si calcoli il periodo del moto di tale sistema, trascurando le forze d’attrito.

R.: 0,54 s ;

Esercizio n. 6

In un motore, un pistone è soggetto ad un moto armonico semplice, avente ampiezza y_o = 7 cm. Se in cima al pistone poggia una rondella e la velocità del motore viene lentamente aumentata, a quale frequenza la rondella non rimarrà più in contatto con il pistone?

R.: 1,88 Hz ;

Esercizio n. 7

A due molle elastiche identiche, di costante elastica   k = 30 N/m  , collegate in serie, è applicata una forza di intensità F = 6,0 N. Quanto vale l’allungamento subito da ciascuna molla? Qual è la costante elastica del sistema costituito dalle due molle?

R.: 0,2 m ; 15 N/m ;

Esercizio n. 8

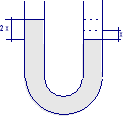
Del mercurio viene versato in un tubo di vetro ad U; normalmente il mercurio raggiunge nelle due colonne la stessa altezza, ma, se disturbato, oscilla avanti ed indietro da colonna a colonna. Un centimetro della colonna di mercurio ha una massa di 15,0 g e, se la colonna subisce lo spostamento descritto in figura e viene poi rilasciata, oscilla avanti ed indietro in condizioni prive di attrito.

Si calcoli:

La costante elastica efficace del moto.

Il periodo di oscillazione.

R.: 29,4 N/m ; 1,16√M s ;

Esercizio n. 9

Una massa  m = 200 g  viene  spinta verso sinistra contro una  molla di  costante elastica   k = 400 N/m,  comprimendola della quantità x = 15 cm rispetto alla sua posizione di equilibrio; il sistema viene poi rilasciato e la massa balza verso destra. Posto che la massa della molla sia molto piccola e considerando trascurabile l’attrito, a quale velocità si muoverà la massa quando abbandonerà la molla?

Supponendo, poi, che la massa m si muova verso sinistra con velocità pari a v_o = 8 m/s e che nell’urtare la molla vi rimanga unita, calcolare la nuova compressione della molla e l’ampiezza della conseguente oscillazione.

R.: 6,7m/s ; 0,18 m ;

Esercizio n. 10

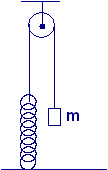
In figura, la massa m = 2,0 kg viene lasciata libera di muoversi quando la molla di costante elastica k = 300 N/m è in quiete. Trascurando l’inerzia e l’attrito della puleggia, oltre alla massa della molla e del filo, si determini:

L’ampiezza dell’oscillazione risultante.

Il punto di equilibrio.

R.: 0,065 m ; 0,065 m ;

Esercizio n. 11

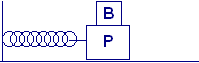
Un blocco P descrive un moto armonico semplice di frequenza f = 1,50 Hz scivolando lungo una superficie liscia orizzontale. 

Un blocco  B  è in quiete, come mostrato in figura,  ed il coefficiente di attrito statico tra i due blocchi è   μ_as = 0,600.

Determinare la massima ampiezza di oscillazione del sistema costituito dai due blocchi, senza che B scivoli su P.

R.: 6,62 cm ;

Esercizio n. 12

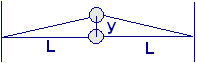
Una massa m è collegata a due elastici uguali, lunghi  L ; su ognuno dei due agisce una tensione T . Si sposta la massa di un piccolo tratto y in direzione verticale; mostrare, assumendo che la tensione T non vari apprezzabilmente, che la forza di richiamo vale –2∙T∙y/L e che il sistema si muove di moto armonico semplice con pulsazione ω = √[(2∙T)/(m∙L)]

R.:

Esercizio n. 13

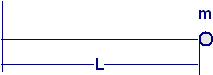
Calcolare la frequenza naturale di oscillazione del sistema rappresentato in figura, costituito da una sbarretta di lunghezza L portante all’estremità una massa m = 1 kg, nell’ipotesi che la massima elongazione sia d = 18,5 mm.

Si supponga la sbarretta incastrata ad un estremo e senza peso. Assumere g = 10 m/s².

R.: 3,7 Hz ;