Possiamo immaginare la massa che crea il campo (Sole oppure Terra) posta nell'origine degli assi, per semplificare le cose dal punto di vista matematico. Consideriamo per fissare le idee la Luna che ruota intorno alla Terra. Sappiamo che secondo la legge di gravitazione universale di Newton, la forza con cui la Terra attira la Luna è direttamente proporzionale al prodotto delle masse e inversamente proporzionale al quadrato della distanza che intercorre fra di esse.
Cerchiamo di esprimere in forma vettoriale la forza gravitazionale modificando leggermente la forma con cui essa viene solitamente scritta che riguarda solo la sua "intensità". Questo ci permetterà di scomporre la forza nelle sue componenti lungo gli assi e quindi di scrivere facilmente le formule per il calcolo ricorrente.
Premettiamo che la posizione della Luna mentre ruota viene individuata da un vettore detto appunto posizione che potrebbe essere rappresentato nel grafico al solito come una freccetta che parte dall'origine (dove si pone la Terra) e la punta sulla Luna. Questo vettore individua ad ogni istante la posizione della Luna; le sue componenti lungo gli assi sono proprio le coordinate della Luna; la distanza Terra Luna è data dal modulo o "intensita'" del vettore posizione.
Ciò posto è facile accettare che la forza esercitata dalla Terra sulla Luna ha la stessa direzione del vettore posizione ma verso opposto (un pò meno facile da accettare è il fatto che questa forza è uguale e contraria a quella esercitata dalla Luna sulla Terra). Un vettore diventa di verso opposto quando lo si cambia di segno come i numeri relativi, mentre se lo si moltiplica per un numero positivo cambia solo la "intensità" o modulo del vettore e non la sua direzione o il suo verso. Quindi il vettore forza gravitazionale deve essere diretto ed avere verso come -r se r è il vettore posizione della Luna.

Quindi abbiamo espresso a parole la conoscenza sia del modulo del vettore forza gravitazionale che della sua direzione e verso, non resta che racchiudere in una sola formula queste informazioni. Ecco la formula vettoriale per la forza:
F = -G·mT·mL·r / (dist)3
dove G costante di gravitazione universale, mT massa Terra, mL massa Luna, r vettore posizione, dist distanza Terra Luna.
Non deve sorprendere che dist appare elevato alla terza perchè se si considera il modulo di r che e ` proprio dist, si semplifica l'esponente e si riottiene la classica formula con il quadrato della distanza. Una versione equivalente è questa:
F = (-G ·mT·mL/dist²) (r/dist)
In altre parole (r/dist) non cambia il modulo ma individua la direzione da dare al vettore.
Questa forza gravitazionale produce una accelerazione sulla Luna data dalla seconda legge della dinamica:
F = mL a
quindi:
a = F/mL = -G·mT·r / (dist)3
Questa formula si può scomporre nelle componenti lungo gli assi:
ax = -G·mT·x / (dist)3 ay = -G·mT·y / (dist)3
A questo punto ci
si
riallaccia con il discorso fatto precedentemente per impostare il
calcolo
ricorrente. Si possono cioè riscrivere le formule per trovare
velocità
e posizione in un intervallino di tempo dt. A partire dalla nuova
posizione
si può calcolare il nuovo valore assunto dalla accelerazione e
riprendere
da capo i calcoli.
Lavorando con la simulazione
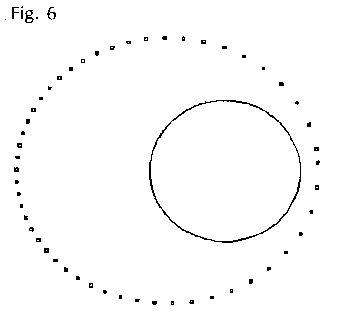
1) Si può far variare la posizione iniziale e la velocità iniziale ottenendo a) caduta inesorabile sulla Terra b) fuga ininterrotta da essa c) orbite chiuse abbastanza stabili.
2) Si possono prendere in considerazione sia il caso di Terra Luna, Terra satelliti artificiali o altri ancora (ad es. Sole Terra)
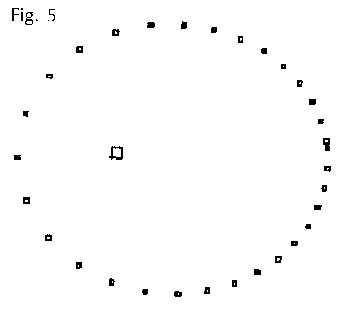
3) Con la simulazione dell'effetto multiflash (disegnare un quadratino ad intervalli regolari di tempo) si può vedere come varia la velocità del satellite al variare della sua distanza dal centro (verifica approssimativa della seconda legge di Keplero).
4) Si può disegnare la celebre figura di Newton con un grave lanciato dallo stesso posto con velocità via via più grandi finchè non entra in orbita.
Concludendo questa simulazione è interessante perchè finalmente, pur con delle inevitabili approssimazioni, si può mettere in rilievo e lo studente può toccare con mano come le equazioni del moto di Newton e la legge di gravitazione universale determinino le orbite dei pianeti, nonchè l'importanza delle condizioni iniziali nell'interpretare i fenomeni fisici. Anche in questo caso l'introduzione di strumenti informatici non ci fa abbandonare i concetti fisici ma ci permette di conoscerli meglio proprio perchè si riesce ad "applicarli" e a vedere delle conseguenze importanti di essi.
indice
successivo
precedente