4. Alcune proprietà degli insiemi PP( )
1. |
Ogni numero N è evidentemente la media degli elementi
di ciascuna delle N/2 coppie di elementi dell’insieme PP(2)
che si trovano in posizioni simmetriche rispetto a N; gli elementi
di tali coppie sono complementari a 2N, nel senso che la somma degli
elementi di ogni coppia è sempre 2N, essendone N la media
aritmetica. |
||||
2. |
I multipli di 3 a partire da 32, costruiti
mediante l’algoritmo 2, ricorrono ogni 6 passi (si tratta
dei soli multipli dispari di 3), pertanto eliminano la primalità
di un elemento su tre dell’insieme PP(2): come conseguenza,
l’insieme PP(2,3) contiene i due terzi degli elementi dell’insieme
PP(2), organizzati a coppie di elementi dell’insieme PP(2)
intervallate da un elemento dello stesso insieme la cui primalità
è eliminata dalla ricorrenza di un multiplo dispari di 3.
L’insieme PP(2,3) è, per costruzione, l’ultimo
degli insiemi PP(2..n) dotato di periodicità perfetta.15 |
||||
3. |
Ogni numero pari 2N precede o segue immediatamente una ricorrenza
di elementi dell’in-sieme PP(2,3);16
se N è multiplo di 3, ogni elemento di PP(2,3)
compreso fra 0 e N è speculare a un elemento di PP(2,3) compreso
fra N e 2N,17
quindi le coppie complementa-ri dell’insieme PP(2,3) in (0,2N)
sono in tal caso i due terzi delle coppie di PP(2) nello stesso
intervallo, vale a dire N/3.18
Se N non è multiplo di 3, il numero di coppie di elementi
di PP(2,3) complementari in (0,2N) dimezza rispetto al caso precedente;19
ne consegue che il numero di coppie complementari di elementi di
PP(2,3) in (0,2N) si riduce a N/6. Come conseguenza, se è
possibile dimostrare che le ricorrenze dei prodotti di ogni i>3,
con i |
||||
4. |
Ogni numero pari Rn=n# è l’estremo superiore di un sottoinsieme, di natura periodica, dell’ insieme PP(2..n); in tale sottoinsieme gli elementi dell’insieme PP(2..n) sono speculari rispetto a Rn/2 entro i limiti descritti dalla proprietà 6.1. Infatti, se si tiene conto dell’algoritmo 1, i gruppi di elementi di PP(i), costituiti da i–1 numeri, ricorrono sia a partire da zero sia a partire da Rn verso zero con passi i identici. Questa proprietà sussiste per la stessa ragione anche per k·Rn con k intero positivo qualunque, quindi la specularità, oltre a essere interna a (0, Rn), sussiste anche in (0, k·Rn), ossia ogni numero k·Rn/2 è asse di specularità (sempre nei limiti della proprietà 6.1) nell’insieme PP(2..n).23
|
||||
5. |
Rn/4 non è intero per definizione,
ma le ricorrenze degli elementi di PP(i) (i=3..n)
sono in posizioni simmetriche per costruzione intorno a tale valore
nell’intervallo (0,Rn/2); tuttavia,
essendo la loro media Rn/4 non intera,
una delle due ricorrenze simmetriche rispetto a Rn/4
è un numero pari; perciò le ricorrenze utili alla
definizione di numeri primi potenziali da parte di PP(i)
(i=3..n) sono in numero metà di quelle
effettive, essendo le ricorrenze pari già tenute in conto
dall’insieme PP(2); ciò che può avere interesse
osservare, quindi, è che le ricorrenze dispari residue sono
speculari, rispetto a Rn/4, solo di numeri
pari. |
||||
6. |
Gli elementi dell’insieme PP(2..n) entrano a far parte dell’insieme P, ossia diventano numeri primi, con le seguenti limitazioni:
|
||||
7. |
I multipli dei numeri interi x definiti come in 6.2,
a partire da p con p numero dell’insieme
PP(2..n) successivo di n, hanno effetto sulla
cancellazione della primalità di alcuni elementi di PP(2..n)
solo per ricorrenze uguali a x2
o maggiori; infatti i prodotti di p, ..., x per
gli elementi di PP(2..n) da 2 a n sono già
comparsi durante la costruzione dei sottoinsiemi da PP(2) a PP(n)
in quanto costruiti secondo l’algoritmo 2, pertanto non hanno
dato luogo a elementi di PP(2..n); come conseguenza le
ricorrenze di multipli di x che cancellano alcuni elementi
di PP(2..n) sono solo quelle che corrispondono alle potenze
di x e ai prodotti di x e sue potenze per tutti
gli elementi dell’insieme PP(2..n) maggiori di x
e per le loro potenze; |
||||
8. |
L’intervallo (0,Rp) contiene p
intervalli di ampiezza Rn essendo Rp
= p·Rn; in ciascuno dei
p intervalli la specularità degli elementi di PP(2..n)
intorno alla mezzeria dell’intervallo stes-so si estende all’intero
intervallo, con le limitazioni poste dalla proprietà 6.1
per il primo e l’ultimo intervallo e dalla 7 per le cancellazioni
dovute ai multipli di p al di sopra di p2
in (0,Rp). Gli elementi di PP(2..p)
sono a loro volta speculari fra p+1 e Rp–(p+1);
le cancellazioni di cui al punto 7 rendono diversi tra loro, in
termini di eliminazioni di primalità, i vari intervalli (k·Rn,(k+1)·Rn)
di ampiezza Rn entro (0,Rp),
ma speculari a coppie rispetto a Rp/2 per
quanto concerne gli elementi di PP(2..p), sempre con l’eccezione
del primo e dell’ultimo a causa della proprietà 6.1.26 |
||||
9. |
La specularità descritta dalla proprietà 4 indica
che contando da Rn a zero si trovano in
progressiva detrazione da Rn elementi PP(2..n)
nello stesso numero e speculari rispetto a quelli che si trovano
contando da zero a Rn, con la sola limitazione
6.1; come conse-guenza la cancellazione dell’elemento di PP(2..n)
dovuta a p2 dista da Rp
di un prodotto di p per un numero intero d che
è primo oppure è un prodotto di numeri primi dell’intervallo
(p, Rn/p)27
e non è una potenza di p;28
a ciò consegue anche che tale distanza, divisa per p,
non è divisibile per i numeri primi da 2 a p; formalmente: |
||||
10. |
Le cancellazioni di elementi dell’insieme PP(2..n)
dovute ai multipli di p sono intervallate come descritto
dall’algoritmo 2 secondo i prodotti di p per se stesso
e per gli elementi dell’insieme PP(2..n) maggiori
di p; anche le cancellazioni interne all’insieme
PP(2..n) avvengono secondo la medesima regola, quindi sono
distanziate a partire da i2
(i=2..n) per prodotti di i per i numeri
di PP(h) maggiori di i.30
L’ultimo elemento di PP(2..n) in (0,Rn)
è sempre Rn–1, quindi (Rn–1)·p=Rn·p–p=Rp–p,
ossia l’ultima cancellazione di elementi dell’insieme
PP(2..n) in (0, Rp) è Rp–p
(di qui la proprietà 6.1). Pertanto i numeri del ciclo p
utili alla cancellazione di alcuni elementi di PP(2..n)
in (0, Rp) sono in quantità uguale
agli elementi di PP(2..n) a partire da p fino
a Rn–1.31
Nell’intervallo (0,Rn)
tali cancellazioni ricorrono evidentemente solo se l’elemento
dell’insieme PP(2..n) interessato è minore
di Rn/p.32 |
||||
11. |
Gli elementi dell’insieme PP(2..n) di (0,Rn)
fino a x, con x>n, sono contro-speculari,
rispetto a Rx/2, degli elementi di (0,Rx)
compresi fra (Rx–x,Rx–2)
per la proprietà 6.1; ciò non ha influenza tuttavia
sull’intervallo (Rn–n,Rn–2),
che per simmetria di posizione (algoritmo 1) può contenere
solo i multipli di tutti i semi fino a n.33
Per la stessa ragione i multipli di x non hanno influenza
sugli omologhi intervalli (di estensione n–2) simmetrici
rispetto a Rn e ai suoi multipli minori
di Rx. Come conseguenza i multipli di x
efficaci ai fini delle cancellazioni, e quindi in grado di causare
ulteriori eventuali contro specularità, si situano nei rimanenti
intervalli
|
||||
12. |
Un numero pari 2N contiene altri fattori primi, oltre a 2, oppure è potenza di 2. Se N contiene un altro fattore primo a, le ricorrenze dei multipli di a sono speculari intorno a N. I multipli del numero primo b che non è fattore di N si situano, per la medesima ragione, specularmente solo intorno al prodotto di b per i fattori di N,38 quindi non presentano specularità intorno a N. Se 2N è potenza di 2, tutti gli altri numeri primi sono del tipo b, quindi le ricorrenze dei loro multipli sono disposte simmetricamente solo intorno ai loro prodotti per la potenza di 2 stessa,39 pertanto non presentano specularità intorno a N. In tutti i casi senza distinzione è dunque evidente che i numeri primi dell’intervallo (0,2N) hanno come simmetrici, rispetto a N, altri numeri primi oppure prodotti di numeri primi compresi nell’intervallo (0,N)40 con le seguenti precisazioni:
|
||||
13. |
Precisazioni sulla disposizione dei numeri pari:
|
||||
14. |
In opportune rappresentazioni “a greca”,45
le ricorrenze dei multipli di p si dispongono lungo le
diagonali di quadrati di lato p. Ogni diagonale individua
su ciascuna delle colonne di primi potenziali una ricorrenza utile
(cancellazione). La “greca”, per rendere evidente questa
proprietà, deve avere modulo 2k·p+1.46 |
Priva di anomalie (intese come assenze di
elementi del ciclo in quanto già considerati in cicli precedenti).
La periodicità è rilevabile anche negli insiemi PP(2..n)
con n > 3, ed è anzi la medesima, solo scalata
in ragione di n, ma interferita (privata di elementi) dalle
ricorrenze dei prodotti di n per i, con 3 |
|
L’Appendice 2 ne dà una visualizzazione immediata. |
|
Ossia i due elementi sono complementari a 2N. |
|
Vedasi anche la proprietà 13 per precisazioni. |
|
Lo spostamento di N di un passo a destra o a sinistra rispetto a un multiplo di 3 rende speculari rispetto a N rispetti-vamente gli elementi di destra e di sinistra di due coppie successive di elementi di PP(2,3), mentre gli altri elementi delle due coppie hanno come complemento un elemento di PP(2) cancellato dalle ricorrenze dei multipli di 3. |
|
Con h numero primo precedente di i. |
|
Con i limiti della nota 12 (proprietà
7) |
|
Questo è un altro enunciato possibile
della congettura di Goldbach come rettificata da Eulero. La tecnica
qui adottata per analizzarla non si basa comunque su questa proprietà,
in sé troppo generica. |
|
La specularità naturalmente
ha termine, a sinistra di k·Rn/2,
con lo zero se non si mette in conto la nota 6. |
|
Vedasi anche proprietà 13. |
|
Si tratta di una contro-specularità
anomala, in cui un numero primo i è in posizione simmetrica,
entro (0,Rn) intorno a Rn/2 , rispetto al proprio multiplo Rn–i.
Es.: con Rn = 210, 205 = 5·41 è contro-speculare di
5 intorno a 105. L’anomalia è costituita dal fatto
che la ricorrenza n·1 è un numero primo. |
|
Gli insiemi PP(2..n) sono sempre
speculari per costruzione intorno a k·Rn/2
(proprietà 4 con la sola limitazione 6.1). Ciò implica
che le cancellazioni dovute a ogni ciclo i < n
a partire da i2 sono in numero pari e che il loro inizio si allontana
dall’origine, e specularmente da Rn, con legge quadratica
o “parabolica”. |
|
p2+p·d=Rp
da cui p+d=Rn, pertanto
d è primo o prodotto di primi maggiori di p
e minori di Rn/p. Se Rn/p<
p, vale a dire se Rn< p2,
allora d è sicuramente un numero primo (ciò
accade solo fino a Rn=30). |
|
p2+pa=p2(1+pa–2)=Rp
è paradossale, infatti (1+pa–2)
= Rp/p2
ha il primo membro intero e il secondo non intero dato che Rp
contiene p solo al primo grado. |
|
La formula Rn–p genera un elemento
di PP(2..n) per definizione, p non essendo fattore di Rn; lo stesso
vale per Rn+p, che ha posizione speculare rispetto a Rn. |
|
Con h numero primo potenziale
immediatamente minore di i nell’insieme PP(h).
Le cancellazioni interne si situano specularmente intorno a Rn
e Rn/2 con la limitazione 6.1. |
|
Tali PP(2..n) includono anche le
potenze di p, mai cancellate fino all’intervento
del ciclo p a partire da p2.
Esempio: gli elementi di PP(2..5), per i quali Rn=30,
utili alla cancellazione di elementi dell’intervallo (0,R7=210)
partono da 7 (prima cancellazione 49) e arrivano a 30–1=29,
infatti l’ultima cancellazione corrisponde al numero 203,
che non cade nella specularità a causa della proprietà
“anomala” 6.1. |
|
Esempio: se n=7, Rn = 210 e p=11; int
(210/11)=19, ossia solo gli elementi di PP(2..n) fino a 19 incluso
a partire da 11, moltiplicati per p, hanno effetto nella cancellazione
di elementi di PP(2..n) nell’intervallo (0,Rn) a causa del ciclo p. In questo caso si hanno quattro cancellazioni sui 49 elementi
di PP(2..n) compresi nell’intervallo. |
|
Quindi x in (0,Rn)
fa necessariamente parte degli elementi speculari rispetto a Rn/2,
ossia è speculare a un numero primo. |
|
Contati evidentemente a partire da zero. |
|
Poiché PP(2,5) contiene come cancellazioni
gli elementi dell’insieme PP(2,3) moltiplicati per 5 a partire
da 52, anche in esso esistono le medesime regolarità cicliche,
tuttavia al negativo trattandosi di cancellazioni. Tali cancellazioni
sono speculari entro (0,R5) con ricorrenze
in PP(2,5), a partire da p2,
distribuite a coppie distanti 4p e internamente di-stanziate
di 2p, ossia con la stessa distribuzione degli elementi
di PP(2,3) scalata della quantità p. Ciò
è vero tuttavia anche per ogni altro elemento di PP(2,3)
maggiore di 5, infatti gli elementi successivamente cancellati non
sono altro che quelli residui di PP(2,3) e quindi ne conservano
la ciclicità, benché interrotta dalle cancellazioni
dovute al ciclo 5. Queste ultime partono da 25 e si susseguono distanziate
ciclicamente di 10 e di 20 passi, quindi cancellano due ele-menti
su 10 in un ciclo di estensione10+20. In altre parole, l’insieme
PP(2,3) rimane dominante. Il ciclo 7, a sua volta, partendo da 49,
ha un periodo di 14+28 elementi, eliminando quindi due elementi
su 14 di PP(2,3), che tuttavia sono ridotti in quanto elementi di
PP(2,5), già privi dei prodotti di 5 e di 7 elevati a qualunque
potenza (Appendice 2). |
|
Vedasi anche nota 12. |
|
Ciò che accade in intervalli più
ampi, ossia le cancellazioni dovute al ciclo y, non ha effetto nell’intervallo
(0,Rn). |
|
Ciascuno con qualunque potenza. |
|
E multipli dei prodotti stessi. |
|
Quelli dell’intervallo (N,2N) sono
evidentemente maggiori di N, quindi non possono avere propri multipli
entro (0,2N). |
|
Tenuto conto del fatto che N può
essere pari o dispari, del fatto che si tratta di divisione intera
e infine dell’“anomalia” costituita dai numeri
1 e 2, queste formule non sono esatte ma solo indicative. |
|
In caso contrario sarebbero fattori di N,
distandone di un multiplo intero di b. |
|
Coppie contate come elementi compresi fra
N e 2N, ossia senza tenere conto delle “anomalie” in
vicinanza dello zero. |
|
Tutte queste regole, in quanto geometricamente
basate sull’algoritmo 1, non tengono conto delle “anomalie”
ricorda-te nella nota precedente. |
|
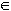 PP(2..h),
per se stesso e per i numeri maggiori di i dell’insieme
PP(2..h)
PP(2..h),
per se stesso e per i numeri maggiori di i dell’insieme
PP(2..h)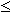 2N/3
fra i numeri di PP(2) contenuti in (0,N) possono far ricor-rere
propri prodotti entro (0,2N); alcuni, vale a dire x
2N/3
fra i numeri di PP(2) contenuti in (0,N) possono far ricor-rere
propri prodotti entro (0,2N); alcuni, vale a dire x