7. Appendice 2
1
La rappresentazione “a greca” può avere qualunque
modulo, in particolare Rn, ma il più signifi-cativo,
ai fini della visualizzazione dell’effetto dei cicli di cancellazioni,
è il modulo R3=2·3, es-sendo l’insieme
PP(2,3) l’unico insieme di primi potenziali “perfetto”.
La costruzione della “greca” di modulo Rn
consiste nel disporre nella prima riga i primi Rn
numeri interi positivi (incluso lo zero), crescenti da sinistra a destra;
nella seconda riga, sotto i primi Rn numeri,
si riportano i successivi Rn numeri e si continua
la numerazione contando ora da destra verso sinistra fino a 2Rn,
che si situa quindi sotto lo zero. E così via, come nelle tabelle
seguenti per il caso Rn = R3 = 6:
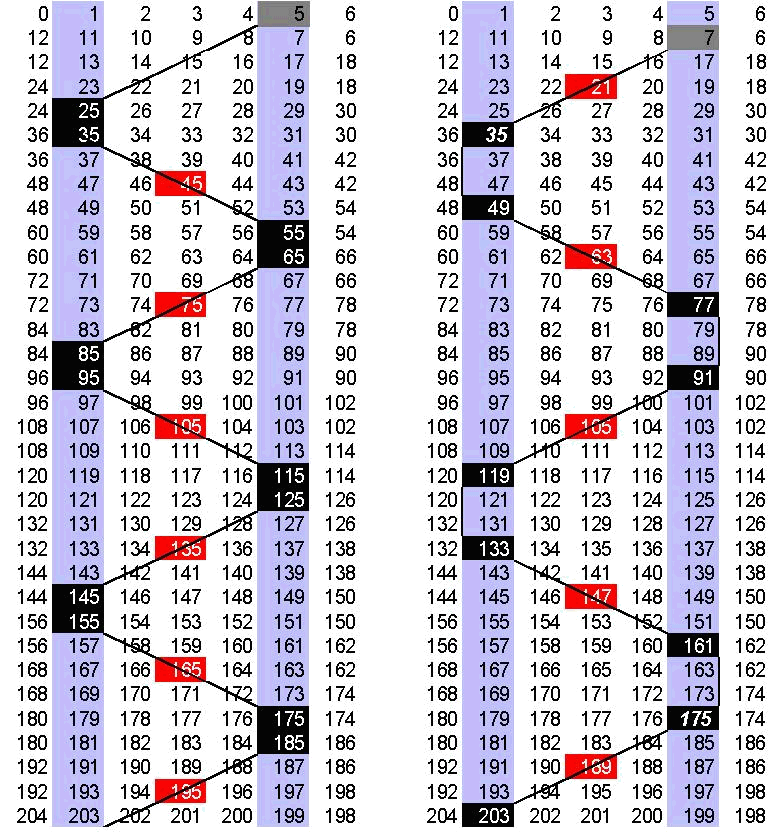
I multipli di 3 risultano incolonnati nelle colonne 3 e 6, mentre gli
elementi PP(2,3) risultano tutti incolonnati sotto 1 e 5, dato che le
altre colonne o sono pari o sono appunto multipli di 3.
Nella “greca” di sinistra si sono indicate con sfondo nero
anche le ricorrenze dei multipli di 5 a partire da 52, che risultano disposte
regolarmente (senza “anomalie”) simmetricamente intorno ai
multipli di 2·3·5; le ricorrenze pari e multiple di 3 risultano
infatti automaticamente escluse, non appartenendo alle colonne 1 e 5.
Nella “greca” di destra, identica alla precedente, si sono
indicate con sfondo nero le ricorrenze dei multipli di 7 a partire da
72, che risultano a loro volta disposte con la medesima regolarità,
sia pure scalata in ragione del fattore 7, ma con anomalie dovute al fatto
che i prodotti di 7 per multipli qualunque di 5 sono già tenuti
in conto nel ciclo 5 (esempio: 175=52·7); le “anomalie”
sono indicate in grassetto corsivo su fondo nero.
Si osserva che la forma “a greca” si conserva, dilatata in
ragione di n, anche nelle ricorrenze di 5 e 7, e questo fatto
è generale quanto ovvio in una rappresentazione di questo tipo;
al crescere di n aumenta solo il numero di “anomalie”
dovute al fatto che le cancellazioni dei prodotti di n per numeri
primi minori di n si sono già verificate nei cicli di
cancellazioni dei numeri primi stessi.
Assunta come asse la colonna del 3, le ricorrenze significative di multipli
dispari di n si dispon-gono sulle colonne 1 e 5 ai vertici di
una “funzione” trapezoidale periodica di periodo (2·3)·2n
(sempre fatte salve le esclusioni dovute ai cicli dei numeri primi minori
di n) e ampiezza 4.59
La ragione di ciò risiede nel fatto che 2·3=Rn
è il passo necessario a queste ricorrenze per cadere nelle colonne
degli elementi di PP(2,3) a partire da n, e nel fatto che esse
distano fra loro alternativamente di 2n e 4n, essendo
escluse le ricorrenze dispari multiple di 3 e quelle pari. Di fatto esse
si dispongono lungo una “greca” dilatata rispetto a quella
originale in ragione del passo n, ma nella quale sono eliminate
le ricorrenze che non cadono nelle colonne 1 e 5.60
L’“aritmia” dei numeri primi è dunque effetto
di cancellazioni di elementi di PP(2,3) che sono di natura in sé
“ritmica” in quanto essenzialmente periodica. In una siffatta
rappre-sentazione, che si limita in realtà a evidenziare una poliritmia,
la verifica del fatto che i numeri pari possano essere sempre la media
di almeno una coppia di numeri primi dipende dunque dall’analisi
delle cancellazioni, della loro architettura e dei suoi “vuoti”,
anziché dei numeri primi in sé.61
Per le stesse ragioni sopra esposte, se si costruiscono “greche”
di modulo 2·(p+1) a partire da zero e di estensione verticale
2k·p, le ricorrenze dei multipli di p
si situano sulle diagonali dei quadrati contigui di dimensioni p·p.
In tali “greche” gli elementi primi potenziali si dispongono
in colonna perché in tali costruzioni tutti i numeri dispari sono
necessariamente incolonnati. La disposizione in diagonale delle cancellazioni
si spiega ovviamente perché nel caso di “greca” di
modulo p i multipli di p si dispongono necessariamente
in colonna, quindi se la “greca” aumen-ta di un passo la propria
larghezza le ricorrenze si sfasano di due passi a ogni ciclo, disponen-do
quindi le ricorrenze su colonne alterne essendo già su righe alterne,
quindi si dispongono esattamente in diagonale. Segue un esempio per p=7,
ma il meccanismo è della massima generalità:
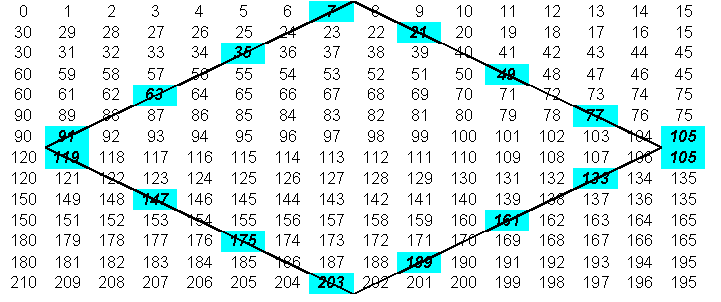
Poiché il modulo dell’esempio contiene i fattori 3 e 5, i
multipli di tali numeri sono necessaria-mente incolonnati. I numeri primi
potenziali si situano quindi tutti nelle colonne 1, 7, 11, 13, e l’intervento
del ciclo 7 causa le cancellazioni indicate, notando che il modulo 15
è R5/2, ossia incolonna tutti gli elementi
di PP(2,3) dell’intervallo considerato, ossia (0,210) nell’esempio,
osservando che 210=R7. In altre parole, in ogni quadrato “a greca”
di lato 2p, contenuto nel rettangolo 2(p+1)·2p, il quadrato costruito
congiungendo i punti medi dei suoi lati è il luogo dei multipli
di p nell’intervallo 2·M·p, con M=2p+1 modulo della
“greca”.
Questo è naturalmente solo un modo più specifico di indicare
quanto già osservato al punto 1 di questa appendice sulla sola
“greca” di modulo 6 in cui, in una forma analoga, la diagonalizzazione
delle ricorrenze si verifica con inclinazione crescente, dato che il modulo
è costante. In quest’altro tipo di rappresentazione a modulo
variabile si tratta sempre di diagonali di quadrati di lati p·p,
che si ripetono identici a ogni duplicazione in larghezza e/o in altezza
della “greca”.
| 59. | La “funzione” è “pari”
nel senso che ha origine nel seme delle ricorrenze, e tale seme
ha uno speculare rispetto allo zero (vedasi nota 6 e proprietà
4). |
| 60. | Per mettere in evidenza questa circostanza
si sono marcate nella tabella anche le ricorrenze che hanno 3 come
fatto-re (caselle evidenziate nella colonna del 3). |
| 61. | Si osservi in particolare che le varie
“funzioni”, incrociandosi in corrispondenza dei prodotti
dei rispettivi semi e dei loro multipli, definiscono intorno a tali
incroci una simmetria “geometrica” di ricorrenze; tale
simmetria si verifica in particola-re intorno ai numeri pari, ma
solo se essi hanno come fattori altri semi oltre al seme 2, e relativa
solo ai semi stessi (proprietà 4.2). |