In questo paragrafo si vuole sviluppare il calcolo analitico del DGD per un sistema a tre lamine, in cui solo la lamina centrale possa ruotare nell'intervallo ![]() gradi , mentre la prima e la terza rimangono ferme in posizione zero.
gradi , mentre la prima e la terza rimangono ferme in posizione zero.
Dapprima si definiscono le costanti di propagazione ![]() e
e ![]() , poi si definisce il DGD introdotto da una singola lamina
, poi si definisce il DGD introdotto da una singola lamina
 |
(4.5.1) |
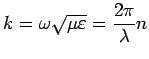 |
(4.5.2) |
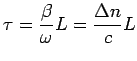 |
(4.5.3) |
| (4.5.4) |
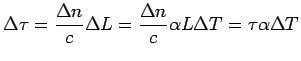 |
(4.5.5) |
Nel formalismo di Müller, per un sistema a due lamine birifrangenti il vettore
![]() di uscita, il cui modulo è il DGD, si scrive nella forma
di uscita, il cui modulo è il DGD, si scrive nella forma
| (4.5.6) |
| (4.5.7) |
Il DGD del sistema a due lamine si trova svolgendo il calcolo del modulo del vettore
![]() , che vale
, che vale
| (4.5.8) |
Nel caso del sistema a tre lamine la relazione risulta lievemente più complicata,
| (4.5.9) |
Nella configurazione scelta la terza lamina è posta a zero, pertanto la matrice di rotazione ![]() diventa in questo caso la matrice identità, e il modulo quadro del DGD si scrive nella forma
diventa in questo caso la matrice identità, e il modulo quadro del DGD si scrive nella forma
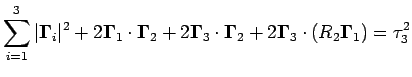 |
(4.5.10) |
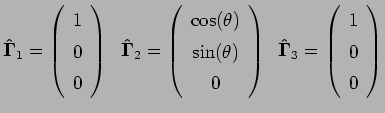
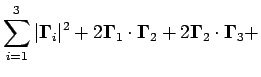 |
|||
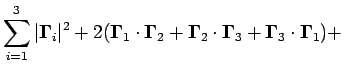 |
|||
| (4.5.11) |
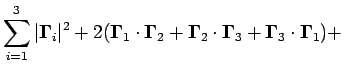 |
|||
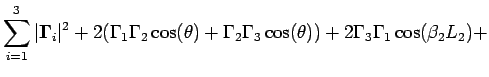 |
|||
| (4.5.12) |
Riordinando i termini e raccogliendo a fattor comune si ottiene la relazione analitica per il DGD in uscita, indicando con
![]() la fase assoluta della lamina centrale. É evidente che l'unico termine dipendente dallo spessore della lamina centrale è la quantità
la fase assoluta della lamina centrale. É evidente che l'unico termine dipendente dallo spessore della lamina centrale è la quantità ![]() appena introdotta, che ci permette di calcolare lo spessore della lamina centrale a partire da misure di DGD,
appena introdotta, che ci permette di calcolare lo spessore della lamina centrale a partire da misure di DGD,