Architettura e musica nel Rinascimento
“...le proporzioni delle voci sono armonia delle orecchie, così quelle delle misure sono armonia degli occhi nostri...”
A.Palladio
Ci soffermiamo ora sullo straordinario connubio tra architettura e musica che si è instaurato nel corso del periodo rinascimentale.
Cesare Brandi osserva che:” La differenza cruciale tra gotico e Rinascimento sta tutta qui: la cancellazione dell’infinito come slancio mistico e dell’infinito come dimensione in cui si sciolgono le guglie gotiche. Lo spazio si rinchiude dentro l’uomo”.
Esiste tuttavia una continuità con il gotico, i temi proposti dagli architetti del rinascimento fiorentino sono tutti profondamente radicati nella cultura medievale; lo stesso Brunelleschi si trova ad operare in un contesto fortemente influenzato dalle tecniche costruttive precedenti.
L’aspetto delle proporzioni assume invece una maggior efficacia, le potenzialità connesse all’utilizzo rigoroso del numero fuorono sviluppate grazie ad un utilizzo più consapevole.
Elemento essenziale di questa concezione artistica è il principio dell’unità, “ tutte le parti di una melodia vengono a trovarsi raccolte in un sol punto in grazia dei rapporti armonici che si stampano nella memoria...ciò che è passato è così vivo nello spirito quanto ciò che viene percepito come presente, e in cui sentiamo preannunciarsi i suoni che si hanno a venire...così l’oggetto esteso, in quanto è artistico, viene concepito e percepito fuori dallo spazio reale, come un tutto che tende a raccordarsi in un sol punto”. (Eva Tea)
Nei trattati di architettura fino al Settecento emergono spesso riferimenti alla musica di tipo proporzionale: perchè l’architettura si rivolge all’arte dei suoni e degli intervalli per trarne delle proporzioni matematiche?
Come sottolineato nel capitolo precedente esisteva fin dall’antichità la convinzione pitagorica che la musica instrumentalis potesse essere riallacciata alla inaudibile musica mundana, quella prodotta dalle schiere celesti. Inoltre l’aritmetica, lo studio dei numeri, la geometria, l’astronomia e la musica costituivano il quadrivium delle “arti” matematiche. Le “arti liberali”, tra cui pittura scultura e architettura, erano considerate attività manuali.
Ecco spiegata quindi la forte esigenza di dare all’architettura un saldo fondamento teorico matematico, ed ecco il motivo per cui gli artisti del quattrocento si sono spesso rivolti alla teoria musicale per trovare la chiave dei loro problemi.
E’ possibile individuare due grandi ambiti in cui si suddivide la ricerca di proporzionalità:il primo è legato all’utilizzo della sezione aurea, il secondo al principio dei piccoli numeri interi.
Nei prossimi paragrafi analizzeremo i presupposti teorici e i risvolti pratici che questi principi hanno avuto nei confronti dell’architettura e della musica.
“Divina proporzione; opera a tutti gli ingegni perspicaci e curiosi necessaria ove ciascun studioso di prospettiva, pittura, architettura, musica e altre matematiche soavissima sottile e ammirabile dottrina conseguirà e dilettarassi con varie questioni di segretissima scienza”
De divina proportione, Luca Pacioli
Un'aura esoterica avvolge da sempre la presenza della S.A. nei più disparati campi del sapere umano.
Si tratta di una porzione di una grandezza corrispondente a poco meno dei due terzi del suo totale (ca. 5/8 o 13/8), in modo che
AB : AC = AC : BC,
la porzione ‘AC’ verrà denominata sezione aurea di ‘AB’.
Tale rapporto matematico in arte è una proporzione riconosciuta come esteticamente piacevole e viene utilizzata come punto di riferimento per la composizione di elementi pittorici, architettonici e come vedremo anche in alcune composizioni musicali.
Al di là del suo fondamento matematico la sezione aurea presenta stretti legami con le proporzioni umane e con moltissime forme naturali, al punto che gli artisti tenderebbero quasi inconsciamente a rispettarne i rapporti.
Moltissimi artisti rinascimentali, tra i quali Leonardo da Vinci, Piero della Francesca e Leon Battista Alberti (autore del trattato “De Architectura”), si dedicarono allo studio e alla teorizzazione delle proporzioni applicandole nelle loro composizioni, proseguendo una tradizione già intrapresa da Vitruvio.
Sezione aurea in musica
I risvolti di questa corrente culturale sono leggibili anche negli sviluppi della musica di quel periodo; a partire dal XIII secolo si avvia un processo di graduale autonomizzazione della composizione musicale rispetto al testo, di pari passo con lo sviluppo della notazione che vede la specificazione non solo dell’altezza della nota ma anche del ritmo: in questo modo la partitura musicale riesce a descrivere sulla carta i suoni proprio come un progetto architettonico è in grado di schematizzare attraverso piante e sezioni una complessa opera tridimensionale.
La musica pratica, dalla connotazione prettamente manuale, assume la pretesa di accostarsi alla sfera delle discipline del quadrivium svincoladosi gradatamente dal testo e avviandosi alla ricerca di leggi matematiche proprie, di rapporti di proporzione che colleghino ogni singola parte con la totalità della composizione.
Oltre che base razionale il numero diviene fonte di una serie di simbologie legate ad un ordine superiore: Il numero tre rievoca l’essenza della Trinità, il quattro le Virtù cardinali, il sette il numero della creazione...
Come la matematica venne a sostituirsi al testo poetico e liturgico?
In primo luogo attraverso l’isoritmia, processo secondo il quale si applica ad una melodia preesistente del tenor una struttura ritmica continuamente ripetuta, suddividendo la voce in tanti piccoli segmenti uguali. Allo stesso modo in architettura lo spazio di una navata viene diviso in un numero di campate di uguale dimensione.
Un criterio a cui la sezione aurea fu particolarmente legata è quello di suddividere la composizione in sezioni proporzionali tra di loro, ripetendo due volte la stessa musica con precisi rapporti di durata tra i due ritornelli. Una melodia proposta in ritmo di 2/4, ad esempio, veniva ripetuta in 4/4 con le durate delle note raddoppiate.
Tinctoris con il trattato Proporzionale musices (1473-74) e Gaffurio (pratica musicae, 1496) giunsero alle più elevate teorizzazioni circa questi metodi.
Il paragone tra musica e architettura con la notazione del ritmo si fa più stretto, venendo la musica ad assumere sulla carta una connotazione a tutti gli effetti spaziale, una composizione diviene un fluire di parti che se nella realtà hanno una durata nella loro rappresentazione sono paragonabili a segmenti di una ben determinata lunghezza.
Nel quattrocento un compositore fiammingo, Guillame Dufay, dà l’avvio per un utilizzo in larga scala della sezione aurea nelle composizioni musicali.
Prendiamo come esempio la sua composizione “Lamentazio Sanctae Matris Ecclesiae Constantinopolitanae”, chanson-mottetto suddiviso in due sezioni corrispondenti alle due ripetizioni del tenor, in cui il ritmo passa (in notazione moderna) da 3/4 a 4/4; in questo modo la prima sezione è sezione aurea dell’intero brano, la seconda è sezione aurea della prima. Inoltre tutti gli altri eventi salienti (cadenze ed entrate delle voci) avvengono secondo precise collocazioni venendo a definire sezioni auree sempre più piccole, a formare una struttura ad incastro come le matrioske.
Un altro caso emblematico si può riscontrare nella Missa Ecce ancilla Domini dello stesso Dufay, nella cui struttura riccorre l’utilizzo della sezione aurea e delle proporzioni aritmetiche.
Essa è composta da tre sezioni: Kyrie, Christe e Kyrie II, distribuiti secondo proporzioni che si ripetono nel Kyrie stesso, di struttura a sua volta tripartita.
Se assegnamo a ciascuna sezione il numero complessivo delle brevi, si possono osservare delle corrispondenze matematiche.
Il Christe e il Kyrie II corrispondono complessivamente (78 brevi) alla sezione aurea del Kyrie, mentre la durata del Kyrie (126 brevi) corrisponde alla sezione aurea del Credo (204 brevi).
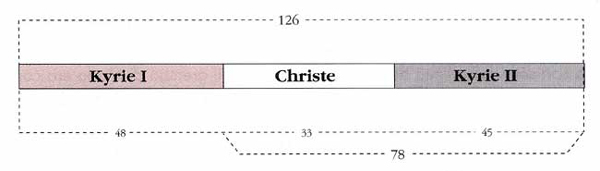
Struttura della Missa "Ecce ancilla domini" di Dufay
L’Agnus Dei ha una durata pari alla somma dei due Kyrie, mentre la somma di Kyrie e Christe sta con quella del Kyrie II e del Gloria nel rapporto di 2:1, ricorrente anche all’interno delle sezioni stesse. Nel rapporto 2:1 interviene anche il numero 33 e i suoi multipli, con evidente riferimento alla vita di Cristo.
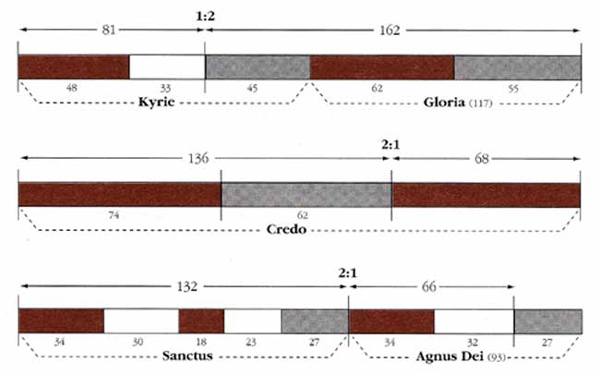
Rapporti tra le varie sezioni della Missa "Ecce ancilla domini" di Dufay
Queste e molte altre relazioni numeriche denotano un interesse per l’aritmetica che concorre alla realizzazione di complesse architetture musicali, in questo modo la Messa, costituita da più sezioni, viene concepita unitariamente.
Non è affatto scontato che queste strutture razionali fossero percepibili all’ascolto, anzi, è probabile che essi non avessero alcun effetto sull’assemblea dei fedeli, ciò che più conta è il significato simbolico di cui esse sono portatrici oltre che del modo di comporre peculiare dei compositori del quattrocento.
La Sezione aurea in architettura
La sezione aurea ebbe i suoi influssi anche sull’architettura del tempo; in particolare Leon Battista Alberti fu il primo importante teorico dell’arte rinascimentale, oltre che costruttore di edifici dallo stile classico puro, fatto di equilibrio e proporzione.
Analizziamo ora alcuni tra i numerosi esempi di architetture ispirate alla divina proporzione.
Per quanto riguarda le opere dell’Alberti, è bene sottolineare come egli non parli mai nei suoi trattati del tipo di proporzionamento utilizzato, quasi volesse tenere segreto il metodo con cui riusciva ad ottenere quell’aspetto di armonioso equilibrio. Tuttavia indagini effettuate con diagrammi e rigorose riproduzioni hanno messo in evidenza che questa sia la regola che domina la connessione di tutte le parti di molte sue costuzioni (es. il tempio Malatastiano a Rimini).
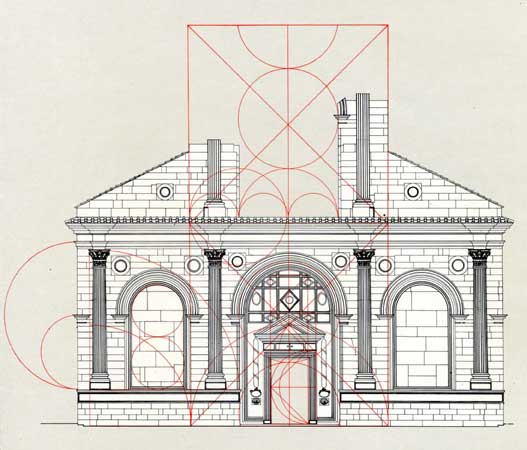
Tracciati proporzionali del tempio Malatestiano di Rimini - L.B.Alberti
Il principio dei piccoli numeri interi
“Di questi numeri si servono gli architetti non confusamente e alla mescolata, ma in modo che corrispondano e consentano da ogni banda all’armonia”
L.B.Alberti
Il proporzionamento armonico dell’architettura del Rinascimento è tutto orientato sul principio generale dell’uso di piccoli numeri interi con i quali organizzare la distribuzione e la disposizione delle varie parti dell’edificio.
Nella musica, disciplina inserita a pieno nel quadrivium delle arti (insieme a geometria, aritmetica e astronomia) si trova conferma delle leggi che regolano il macrocosmo e il microcosmo rivelate da Pitagora e da Platone.
Di qui nasce la convinzione che l’architetto non sia in nessun modo libero di applicare all’edificio uno schema casuale di rapporti, ma che tali rapporti debbano conciliarsi con un sistema di ordine superiore, le proporzioni devono esprimere l’ordine cosmico e la musica diviene mezzo privilegiato per innalzare la disciplina architettonica al livello delle arti del quadrivium.
Le proporzioni corripondenti agli intervalli musicali vengono così trasposte nella progettazione degli edifici divenendo la base di veri e propri reticoli modulari, così come un’orchestra accorda gli strumenti sulla nota “la” per poi intonare, attraverso intervalli armonici, accordi che suonano bene all’orecchio.
Fin dai tempi più antichi si è rilevato che due note suonano bene insieme quando i rapporti tra le loro frequenze sono caratterizzati da piccoli numeri interi, Pitagora definisce la cosidetta tetraktis, comprendente i numeri 1,2,3 e 4, la cui somma è 10 (simbolo del Demiurgo).
Premesse matematiche
La teoria delle proporzioni alla base dei tracciati armonici dell'architettura, ha radici molto profonde, che affondano probabilmente nei contatti con l'antica civiltà egizia, ma è nella Grecia del VI secolo a.C. che ne viene definita la base dottrinale, con l'introduzione da parte di Pitagora della filosofia matematica.
In greco il concetto di relazione si esprimeva in termini matematici come rapporto a:b. Dalla combinazione di due o più relazioni si originava la proporzione, espressa dall'equazione generale a:b=c:d (proporzione disgiunta), oppure, nel caso in cui le due grandezze intermedie b e c fossero state uguali, a:b=b:c (proporzione continua).
Pitagora e i suoi discepoli stabilirono tre tipi principali di proporzione:
- la proporzione aritmetica c-b=b-a (es: 1, 2, 3),;
- la proporzione geometrica a/b=b/c (es: 1, 2, 4),;
- la proporzione armonica (b-a)/a=(c-b)/c (es: 2, 3, 6),.
A queste tre proporzioni corrispondono, rispettivamente, la medietà (o media) aritmetica b=(a+c)/2, la medietà geometrica b=÷ac, e la medietà armonica b=2ac/(a+c). Questa interpretazione trovava delle incoraggianti conferme nello studio della musica; infatti considerando i due toni che definiscono l'intervallo di ottava (do grave e do acuto) come termini estremi a e c di una proporzione, risulta che, essendo essi in rapporto di 1/2, la loro media aritmetica è b = (2+1)/2 = 3/2 mentre la loro media armonica è b = 2(2¥ 1)/(2+1) = 4/3.
L'intervallo di quinta è quindi la media aritmetica tra due toni distanti di un’ottava, mentre quello di quarta ne è la media armonica. Quanto alla proporzione geometrica, essa mette in relazione le due medie, essendo 2 : 4/3 = 3/2 : 1.
Premesse fisiche
E’ bene sottolineare quali sono le premesse fisiche per cui si passa dalla produzione di suoni alla rete di numeri interi.
La prima osservazione è che a ciascuna nota corrisponde una determinata frequenza proporzionata alla sua altezza;se andiamo a misurare l’ intervallo, ossia la distanza fra due note, calcolando il rapporto fra le loro frequenze, ci accorgiamo che questo rapporto è sempre lo stesso per coppie di suoni alla stessa distanza nella scala musicale.
All’intervallo di ottava corrisponde ad esempio il rapporto 2, alla quinta il rapporto 3/2 e così via.

Rapporti tra intervalli e frequenze nella scala musicale.
Lo stesso principio è stato osservato da Pitagora, il quale si rese conto che faendo vibrare una corda tesa tra due estremi è possibile udire assieme ad essa una serie di suoni (le armoniche) che formano con la nota fondamentale accordi piacevoli all’orecchio. E’ possibile ricercare questi suoni intercettando la corda in diversi punti lungo la sua lunghezza: se la intercettiamo a metà otteniamo l’ottava, a 2/3 la quinta, a 3/4 la quarta e così via)

Rapporti tra suoni, frequenze, lunghezza di una corda vibrante
Da questo studio Pitagora ricavò la lambda, triangolo formato da numeri doppi e tripli con cui è possibile ricavare tutte le armonie musicali.
Dovunque quindi si incontrino rapporti della serie 6,8,12,16,18,24...si può supporre che ci sia il preciso intento di emulare le proporzioni musicali.
L’individuazione di questi criteri è spesso difficile e non attribuibile con certezza ad una consapevole volontà del progettista, è bene tenere presente che per fare questo tipo di analisi è fondamentale “tradurre” le misure riscontrate negli edifici secondo le unità di misura del tempo.
Osservazione
Il connubio tra architettura e musica costituito dal principio dei numeri piccoli si realizza sul piano puramente logico-razionale, gli architetti attingono alla musica come fonte di intervalli matematici e non come sorgente di sonorità piacevoli all’orecchio.
Non è affatto rilevante come questi intervalli si compongano tra loro a produrre armonie musicali, poichè gli artisti non intendevano tradurre la musica in architettura, anzi spesso i numeri interi che generano la rete modulare darebbero luogo in musica a delle dissonanze.
Si prendano ad esempio le progressioni Albertiane 4:6:9 e 9:12:16, la prima è una sequenza di due quinte (es. do-sol-re), la seconda di due quarte (es.do-fa-si), ossia sono dal punto di vista musicale delle dissonanze.
|