Triangolo di perimetro minimo inscritto in un triangolo acutangolo
Fagnano dal nome del matematico che lo risolse nel settecento.
Problema di Fagnano Triangolo ortico di Giuseppe Ferrero che cita:
Per esaminare il problema del perimetro minimo con GeoGebra si può procedere nel seguente modo:Figura 1
Si disegni un triangolo acutangolo ABC qualunque
Si definisca un punto P su AB
Indichiamo con P1 il simmetrico di P rispetto il lato BC e con P2 il simmetrico di P rispetto il lato CA
Disegnamo il segmento P1 P2 e individuiamo i punti di intersezione con i lati BC e CA. Siano essi rispettivamente M ed N
Il segmento P1 P2 ha la lunghezza del perimetro del triangolo PMN
Scegliendo due altri punti Y e Z qualunque su AC e su BC, il perimetro del triangolo PYZ risulterà dalla lunghezza della spezzata P2 YZP1 maggiore di P1 P2
Indicando con γ l'angolo in C del triangolo ABC, l'angolo P2 CP1 risulterà costantemente 2γ
I lati di questo angolo sono uguali a CP=CP1 =CP2
Ma allora il perimetro minimo si otterrà quando CP sarà minimo cioè quando P sarà il piede della perpendicolare ad AB condotta da C
Con GeoGebra è facile verificare che PMN ha il perimetro minimo facendo variare Y, Z ed anche P. Quando P sarà il piede dell'altezza relativa ad AB, si ottiene il perimetro minimo
Caratteristiche del triangolo ortico
Figura 2 1 , M1 e P sono i piedi delle tre altezze del triangolo ABC.1 G e CGN1 hanno l'ipotenusa in comune CG, quindi si può disegnare la circonferenza per tre punti C, M1 , G che passerà anche per C, G, N1 1 CG uguale all'angolo N1 M1 G.Figura 3 1 A e APC aventi entrambi ipotenusa comune AC.1 P sono uguali perchè insistono entrambi su AP.1 M1 A e AM1 P sono entrambi uguali all'angolo ACP.1 è bisettrice dell'angolo N1 M1 P.1 A retto e l'angolo N1 M1 A dato da (90-α), si deduce che l'angolo CM1 N1 è uguale ad α.1 M1 C ha gli stessi angoli del triangolo ABC:1 M1 = β1 M1 C = α1 B è retto e l'angolo AM1 P= (90-α), segue che l'angolo PM1 B = α.Figura 4 1 N1 ottenuto congiungendo i piedi delle altezze del triangolo ABC ha gli angoli interni dati da:Figura 5
Le altezze del triangolo ABC sono le bisettrici del triangolo ortico.Figura 6
Triangolo ortico con la trigonometria
I risultati precedenti sul triangolo ortico si possono trovare anche utilizzando la trigonometria.1 N1 sono proporzionali a quelli di ABC.1 N1 , M1 PB e N1 PA.1 . Considerando il triangolo N1 BC si ha:1 = a sen(90-γ) = a cos(γ)1 = b sen(90-γ) = b cos(γ)1 C/CM1 = a/b1 C sta opposto all'angolo α come a e CM1 sta opposto all'angolo β come b.1 M1 :1 M1 2 = a2 cos2 (γ)+ b2 cos2 (γ)- 2 a b cos3 (γ) = cos2 (γ) (a2 +b2 -2 a b cos(γ)) = cos2 (γ) c2 .1 PB si deduce che l'angolo PM1 B = α e M1 PB = γ.
Triangolo di perimetro minimo
Per dimostrare che il triangolo ortico ottenuto congiungendo i tre piedi delle altezze di ABC è il triangolo inscritto in ABC di perimetro minimo partiamo dalla seguente figura:Figura 7 1 P la simmetria rispetto il lato BC e a N1 P la simmetria rispetto il lato AC.1 e M1 non sono scelti come prima come punti di incontro del segmento P1 P2 con i lati BC e AC; essi sono invece i piedi delle altezze relative ai lati AC e BC.2 N1 M1 P1 appartengono alla stessa retta.1 B è uguale, perchè ottenuto con una simmetria assiale, all'angolo BM1 P.1 B è uguale all'angolo CM1 N1 .1 P è uguale all'angolo N1 M1 C.1 e M1 B giacciono sul lato BC, si conclude che i due angoli BM1 P e N1 M1 C sono opposti al vertice e quindi M1 P1 e N1 M1 giacciono sulla stessa retta.2 è allineato a N1 M1 completando la dimostrazione. inizio indice generale
 Figura 1
Figura 1 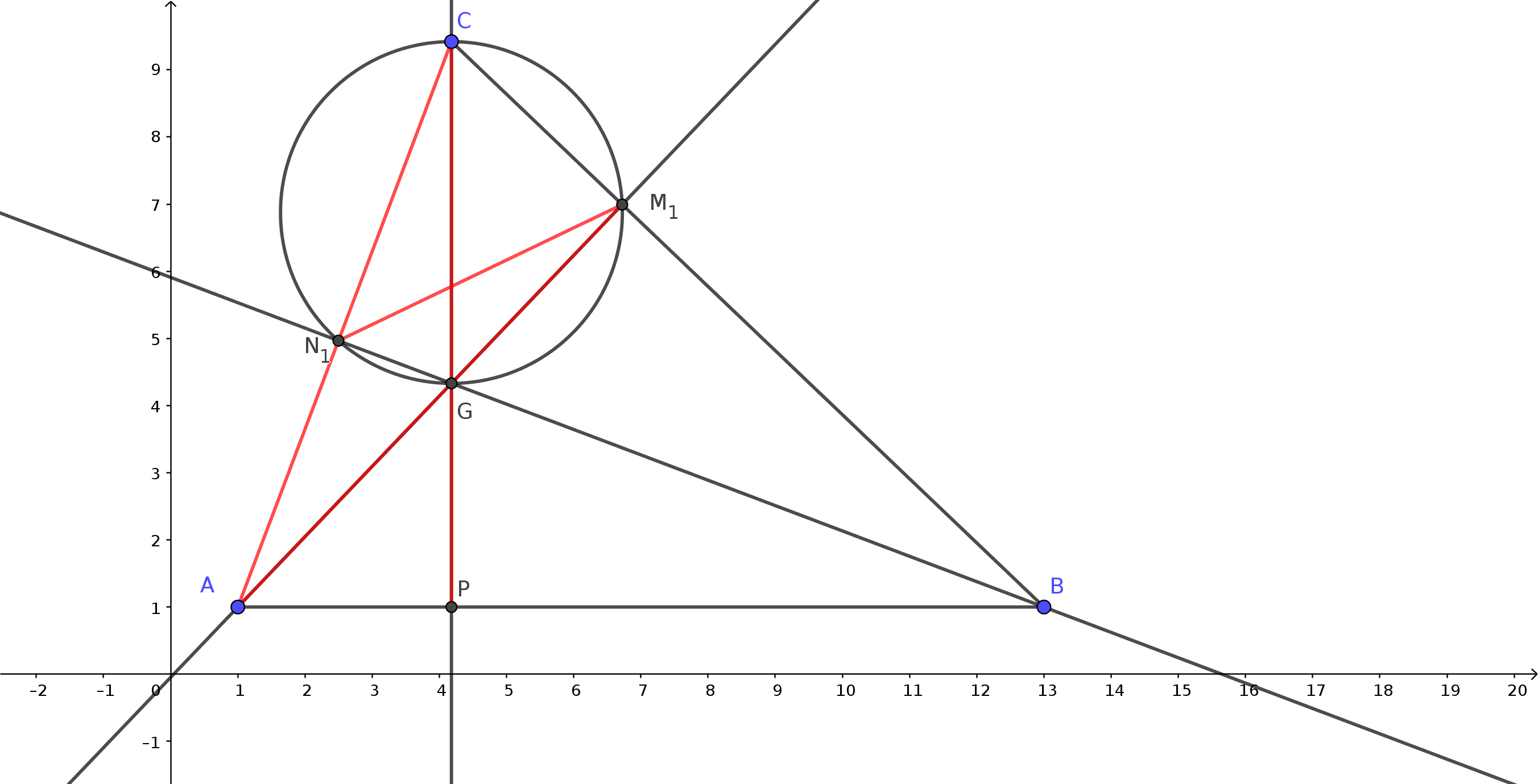 Figura 2
Figura 2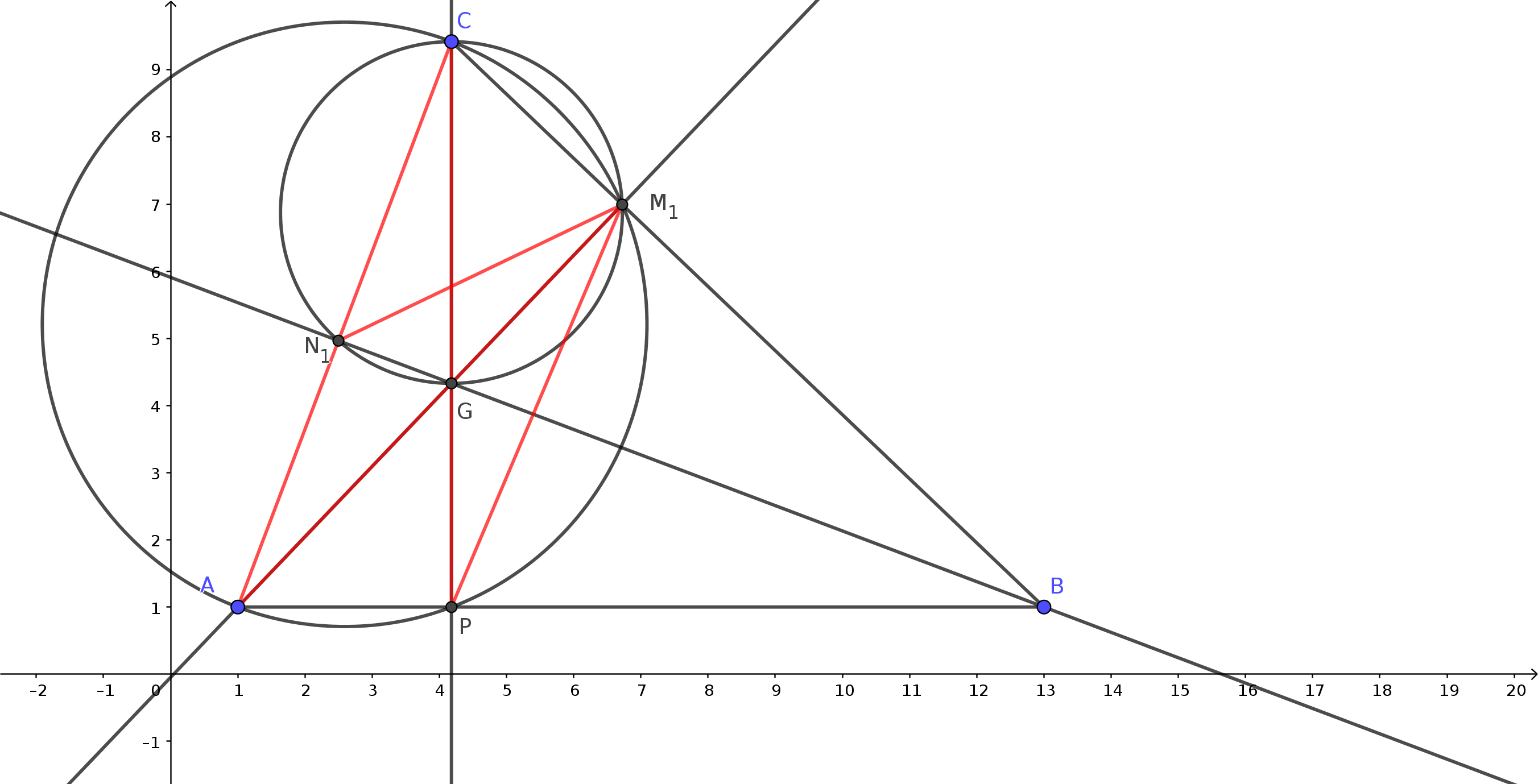 Figura 3
Figura 3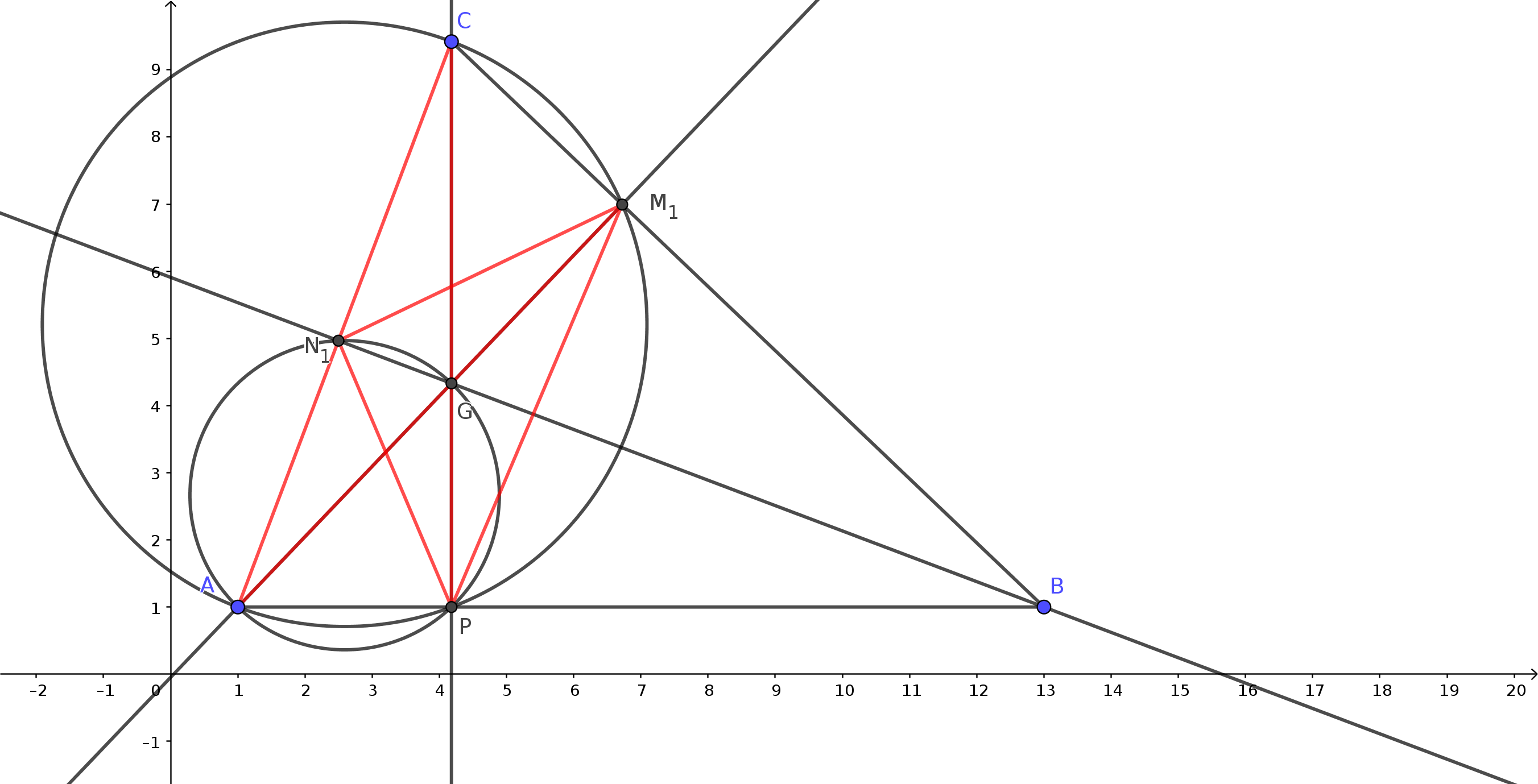 Figura 4
Figura 4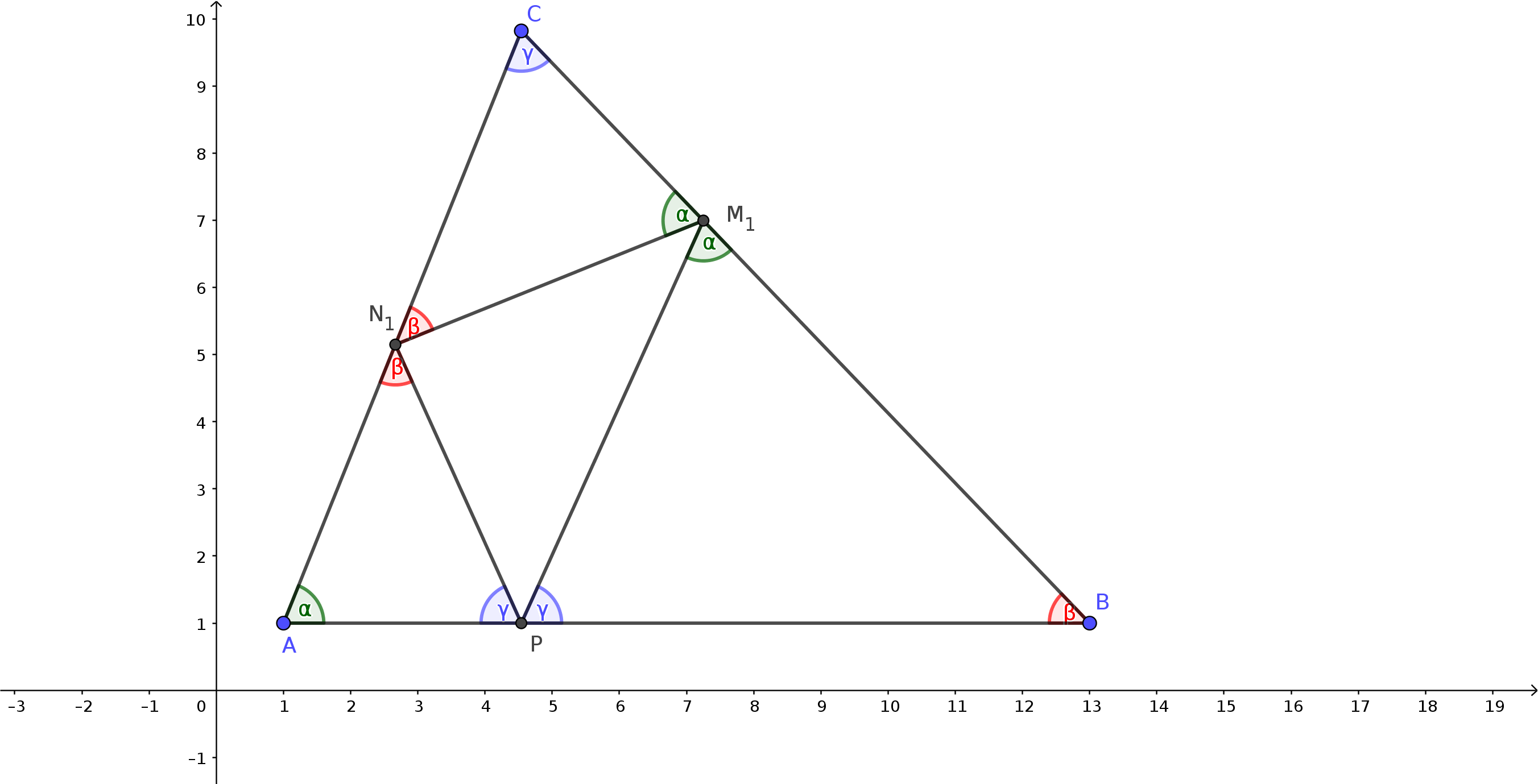 Figura 5
Figura 5 Figura 6
Figura 6 Figura 7
Figura 7