 |
Quando disegniamo dei poligoni regolari (triangolo equilatero, quadrato, pentagono, decagono) non vi sono ripensamenti perché i lati sono tutti uguali. Invece per un poligono non regolare (triangolo isoscele, rettangolo, trapezio) bisogna stabilire un rapporto fra larghezza e altezza e qui incominciano i dubbi o i ripensamenti per quanto riguarda l’estetica. E’ più estetico o armonico un rettangolo che si scosti poco dal quadrato oppure un rettangolo molto allungato? Ecco i due casi estremi:
 |
La soluzione a questo dilemma l'aveva già data Euclide stabilendo una particolare proporzione come segue: "si può dire che una linea retta sia stata divisa secondo la proporzione estrema e media quando l'intera linea sta alla parte maggiore così come la maggiore sta alla minore":
 |
Gli antichi greci usavano, consciamente o inconsciamente, questa proporzione per ottenere un'immagine estetica inserendola in particolare nel rettangolo: il rapporto fra il lato lungo a e il lato corto b deve essere uguale a 1,618:
 |
Dopo 2200 anni da questa scelta si è voluto verificare se il senso estetico dell’uomo moderno corrisponda ancora ai vecchi canoni. In un esperimento statistico è stato mostrato a più persone vari rettangoli con diversi rapporti, poi è stato chiesto di indicare quale rettangolo avesse destato in loro una maggior sensazione armonica. I risultati ottenuti indicano una certa preferenza (non molto marcata a dir il vero) verso l’antico rapporto a : b = 1,618.
Gli architetti dell'antica Grecia percepivano inconsciamente
un’armonia in questo rapporto mentre i matematici lo hanno
scoperto non con un’indagine statistica ma tramite la
matematica e la geometria. Infatti una espressione algebrica che
tiene conto contemporaneamente del concetto di rapporto e di
proporzione da come risultato 1,618. Riassumiamo brevemente
questi due ultimi concetti:
Rapporto: è il quoziente di due valori,
esempio:
| 100 / 25 = 4 | 21 / 7 = 3 | a / b = c |
Proporzione: due insiemi di numeri si dicono proporzionali fra loro quando hanno lo stesso rapporto e si scrivono così:
| 100 / 25 = 28 / 7 | a / b = c / d | a : b = c : d |
L’espressione algebrica a:b = c:d contiene sia il concetto di rapporto che di proporzione ma non è ridotta ai minimi termini perciò ha infinite soluzioni. Platone diceva che per esprimere una proporzione bastano tre elementi, ma anche in questo modo otteniamo infinite soluzioni. Per avere una sola soluzione è necessario ridurre gli elementi a 2 tramite un trucco. Infatti se noi poniamo c = a + b mettiamo in gioco solo due valori. Ecco l’espressione algebrica ridotta ai minimi termini che contiene contemporaneamente rapporto e proporzione e ha come unica soluzione 1,618:
| a / b = b / (a + b) |
Per queste sue caratteristiche (rapporto, proporzione e una
sola soluzione) può meritarsi l'appellativo di "proporzione
aurea" o meglio "sezione aurea" e il
risultato (1,618) nelle formule si esprime con la lettera greca F. Luca
Pacioli, amico di Leonardo, la denominò "la divina
proporzione". Ma la magia della sezione aurea continua nella
matematica con un gran numero di combinazioni particolari. Per
esempio 1,618 x 1,618 =
2,618 e 1:1,618 = 0,618 inoltre nella serie dei numeri del
Fibonacci la progressione è cadenzata da F.
Per facilitare la soluzione
delle espressioni algebriche a volte si usa dare il valore
"1" a un termine. Nel nostro caso a = 1. Ecco i
vari passaggi per ottenere la soluzione:
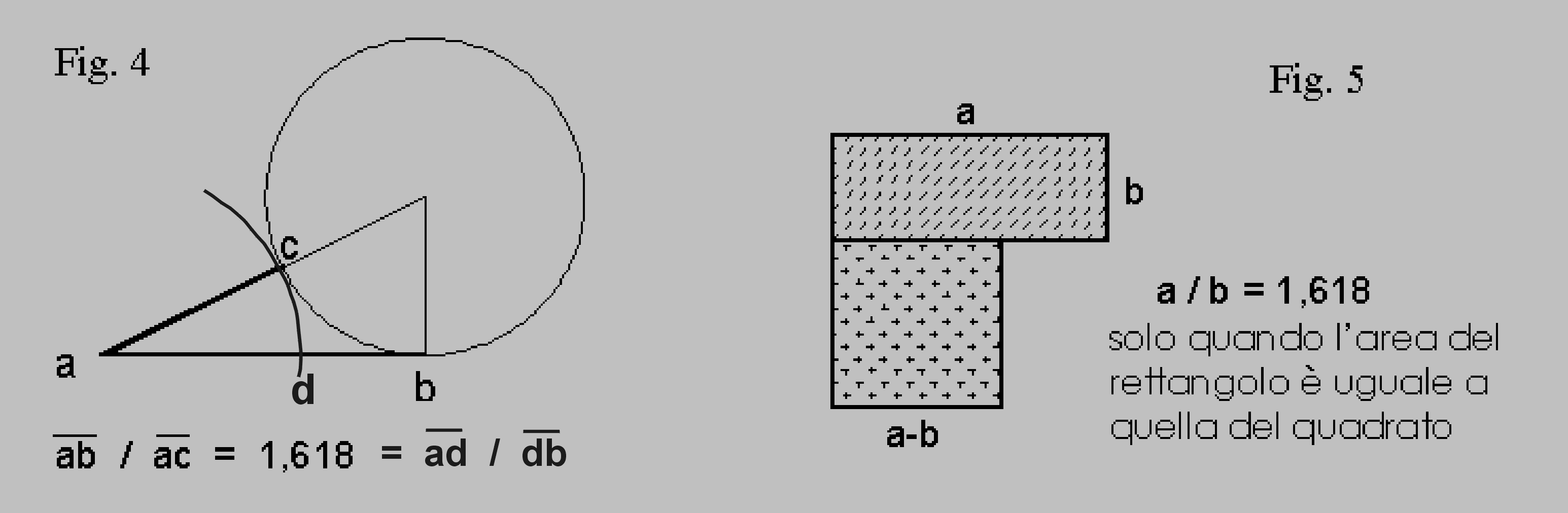
Anche la geometria ha "voce in capitolo" infatti basta tracciare un triangolo rettangolo con un cateto lungo il doppio dell’altro e un cerchio per ottenere un segmento in rapporto aureo col cateto maggiore come mostra la fig. 4, invece la fig. 5 indica come ottenere la sezione aurea giocando sull’area del rettangolo e del quadrato:
 |
Senza entrare in dettagli elenchiamo altri campi dove si
incontra la sezione aurea:
- nelle proporzioni del corpo umano
- nei templi antichi, nelle chiese romaniche e nelle cattedrali
gotiche
- nella piramide di Cheope
- in alcuni vasi antichi e in alcune opere architettoniche e
artistiche
- nella dinamica di crescita di molti vegetali
- nella spirale logaritmica formata da alcune conchiglie marine
- in alcune forme geometriche come il pentagono e il decagono
La sezione
aurea, come abbiamo visto, si insinua in tutti i regni
della natura, perciò questa sua polivalenza la fa
assurgere all’altezza di "archetipo". |
In geometria il pentagono e il decagono sono i poligoni regolari che meglio esprimono la sezione aurea F, mentre la grande piramide di Cheope contiene sia F che Ö F (radice di F) come mostrano queste figure:
 |
I pitagorici aveva adottato come simbolo (oggi diremo come "logo") la stella a cinque punte perciò si suppone che fossero a conoscenza anche del rapporto aureo, ma essendo quest'ultimo un numero irrazionale veniva ignorato.
Nei regni dalla vita invece domina la spirale logaritmica che ha un ritmo di sviluppo legato a F (sezione aurea) e un altro tipo di spirale il cui sviluppo è legato a Ö F (radice di F). Questi due tipi di spirali sono l’archetipo della forma di molte conchiglie e anche del ritmo col quale spuntano i rami laterali di molti vegetali e la disposizione dei loro semi nei fiori.
 |
Anche un particolare triangolo isoscele legato alla sezione aurea
può essere usato per tracciare una spirale logaritmica. Lo si
ricava dal pentagono e bisecando uno dei due angoli di 72° si
ottiene un triangolo più piccolo ma con gli stessi angoli del
primo come mostra la seguente figura:
 |
Nella figura qui sopra si può notare che il punto C divide il
lato AB del triangolo secondo il rapporto aureo e che per
costruire la spirale è stato necessario bisezionare il triangolo
piccolo per ottenerne un altro più piccolo ancora e così via
per più volte.
Esiste anche un particolare angolo detto "aureo" che si
ottiene con la seguente formula: 360 - 360 / F
= 137,5 077 (F = sezione aurea).
In botanica viene detto "angolo di divergenza" perchè
rappresenta la crescita radiale dei semi di molti fiori. Questi
semi sono così compatti, spazialmente, in virtù di questo
angolo di divergenza. L'esempio più bello è il girasole nel
quale la disposizione dei semi, forma spirali destrose e
sinistrose.
Il corpo umano, capolavoro del creato, non fa eccezione, ecco
alcuni rapporti legati a F :
 |
| prossimo capitolo: | 3 - I cinque solidi platonici | Indice |