Lezione 7

*Il tempo proprio e la quadrivelocità*

di Michele Moroni

IL TEMPO PROPRIO

Consideriamo una particella massiva che si muove nello spazio. La sua traiettoria è ovviamente di tipo timelike, dato che dt²>dx²+dy²+dz² in ogni istante. Scriviamo quindi la precedente disuguaglianza nella forma ds² = -dt²+dx²+dy²+dz² < 0

Abbiamo già visto (lezione2) che l'intevallo spazio temporale è lorentz invariante.

Sapendo che dx²+dy²+dz² rappresenta il modulo quadro dello spostamento infinitesimo della particella nello spazio ordinario (dl) possiamo scrivere

ds² = -dt²+dl²

da cui

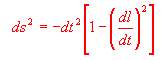
Sapendo che ds² è sicuramente negativo, introduciamo la grandezza

dt²=-ds²

Questa è certamente positiva. Osservando inoltre che dl/dt non è altro che l'ordinaria velocità della particella si può scrivere:

(convenzionalmente il segno di dt si assume positivo per particelle ordinarie. Vedremo più avanti che cosa succede per le antiparticelle)

Essendo il ds² di una particella lorentz invariante anche dt è una quantità scalare indipendente dal sistema di riferimento preso; questa viene chiamata intervallo infinitesimo di tempo proprio

Si puo' quindi definire il tempo proprio di una particella ad un determinato istante come:

1)

( è forse superfluo ricordare che anche questa quantità è chiaramente uno scalare lorentz invariante)

Che cosa rappresenta il tempo proprio? Per rispondere a questa domanda basta considerare la traiettoria della particella dal punto A=[0,0,0,0] al punto B=[t,x,y,z]. Il tempo proprio t della particella all'istante t è quindi dato dalla formula 1). Se ci poniamo in un sistema di riferimento O' solidale alla particella i vettori A e B avranno coordinate A'=[0,0,0,0] e B'=[t',0,0,0]. Il tempo proprio assumerà quindi l'espressione:

ma, essendo il tempo proprio lorentz invariante, t = t'= t' in ogni sistema di riferimento; quindi il tempo proprio rappresenta il tempo misurato in un sistema di riferimento solidale alla particella.

LA QUADRIVELOCITA'

Consideriamo la nostra particella massiva e identifichiamo ogni punto della sua traiettoria nello spazio-tempo con un quadrivettore posizione [t,x,y,z]. introduciamo quindi il quadrivettore spostamento infinitesimo

ds = [dt,dx,dy,dz].

Questo quadrivettore è chiaramente tangente alla traiettoria della particella, inoltre, dato che la traiettoria è timelike (vedi lezioni 2 e 3), il suo modulo quadro è invariante lorentziano negativo. ds può essere scritto come

ds = dt [1, (dx/dt), (dy/dt), (dz/dt)]

dx/dt, dy/dt, dz/dt non sono altro che le componenti lungo le direzioni x, y, z dell'ordinaria velocità tridimensionale (ricordiamo dimensionata rispetto a c). Quindi

ds = dt [1, v_x ,v_y ,v_z]

Consideriamo ora il rapporto

U è chiaramente un quadrivettore avente stessa direzione di ds, e quindi tangente alla traiettoria della particella. Inoltre ||U||²è lorentz invariante, dato che lo sono ds e dt.

Il modulo quadro di U si calcola facilmente

Quindi, riassumendo...

Indice Lezioni - Lezione Precedente - Lezione Seguente