|
Consideriamo una quaterna di grandezze [A0, A1, A2, A3] in un sistema di riferimento O. Successivamente misuriamo le stesse grandezze [A0', A1', A2', A3'] in un sistema di riferimento O' in moto con velocità V=Vx rispetto ad O. Se la relazione esistente tra le grandezze è la seguente
allora si dice che la precedente quaterna forma un quadrivettore |
In generale le componenti di un quadrivettore vengono indicate con l'indice esponente (le ragioni di questa scelta saranno chiare tra poche righe).
La legge di trasformazione delle componenti di un quadrivettore (1) viene usualmente scritta in forma contratta come:
![]()
In questa espressione è sottointesa una sommatoria da 0 a 3 sull'indice muto b. Il simbolo Lab indica l'elemento della matrice di trasformazione determinato dalla riga a e colonna b.
Un' importante proprietà della matrice (1) è la seguente:
![]()
Dove il simbolo dna (simbolo di Kroneker) è uguale a 1 se n=a, mentre è uguale a 0 in caso contrario. La prececente espressione ci dice che il prodotto righe per colonne tra la matrice L e quella ottenuta da L sostituendo v con -v è uguale alla matrice identità I. Conseguentemente la matrice ottenuta da L effettuando la trasformazione (v) --> (-v) è l'inversa di L
E' quindi verificata la relazione
![]()
o, se si preferisce
![]() (2)
(2)
Per ogni insieme di grandezze quadrivettoriale è estremamente utile introdurre i cosiddetti "vettori di base".
e0=[1,0,0,0]
e1=[0,1,0,0]
e2=[0,0,1,0]
e3=[0,0,0,1]
(i vettori di base in generale si indicano con l'indice deponente)
Conseguentemente un generico quadrivettore [A0, A1, A2, A3] può essere scritto come
[A0, A1, A2, A3] = A0e0+A1e1+A2e2+A3e3 = Aaea
(nell'ultimo passaggio è sottointesa, come usuale, una sommatoria su indici ripetuti)
LEGGE DI TRASFORMAZIONE DEI VETTORI DI BASE
Consideriamo il vettore di base e1 nel sistema di riferimento O. Applicando la trasformazione di Lorentz (1) otteniamo l'espressione di questo vettore di base nel sistema di riferimento O'.
![]()
Generalizzando i precedenti passaggi al caso di un generico vettore di base eb possiamo immediatamente scrivere la legge di trasformazione dei vettori di base come
![]()
o se si preferisce...
![]()
Allo stesso modo posso considerare il vettore di base e1 nel sistema di riferimento O'. Applicando la trasformazione di Lorentz inversa (2) otteniamo l'espressione di questo vettore di base nel sistema di riferimento O
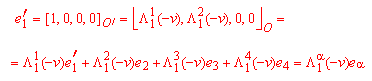
Da cui, generalizzando ad ogni vettore di base
![]()
O analogamente....
![]()
Ricapitolando, le equazioni di trasformazione sono:
|
Dirette
|
Inverse
|
|
|
|
|
|
Altre importanti proprietà dei quadrivettori sono le seguenti.
