1)
In questo caso si dice che la curva Ŕ di tipo tempo (time-like) |
2)
In questo secondo caso si dice che la curva Ŕ di tipo spazio (space-like) |
3) In quest'ultimo caso la curva Ŕ di tipo luce |
Lezione 3
*Il cono di luce*
versione 2.0 28 dicembre 2003
Consideriamo una curva L nel diagramma spazio tempo [f(t, x,y,z)=0], e due punti generici a distanza infinitesima posti su L. Calcoliamo quindi l'intervallo spazio-temporale tra questi due punti.
Si possono verificare le seguenti 3 possibilitÓ:
1)
In questo caso si dice che la curva Ŕ di tipo tempo (time-like) |
2)
In questo secondo caso si dice che la curva Ŕ di tipo spazio (space-like) |
3) In quest'ultimo caso la curva Ŕ di tipo luce |
Nota: per tutte le curve di interesse fisico il segno di ds2 Ŕ invariante rispetto al punto in cui si misura.
Analizziamo ora le curve di tipo luce
la condizione ds2=0 puo' essere riscritta come
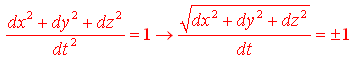
Al primo membro abbiamo il rapporto tra lo spazio percorso in un intervallo di tempo infinitesimo (espresso in secondi-luce) e l'intevallo di tempo stesso. Ma questa non Ŕ altro che la definizione di velocitÓ istantanea. Conseguentemente le particelle che si muovono lungo una traiettoria di tipo luce sono quelle che soddisfano la relazione švš=1 e quindi i fotoni.
Si deduce quindi immediatamente:
La luce si muove nel diagramma spazio-tempo seguendo traiettorie che annullano l'intervallo spazio-temporale
Il luogo geometrico dei
punti dello spazio-tempo che soddisfano la condizione ds2=0 Ŕ
chiamato convenzionalmente
CONO DI LUCE
(anche se, formalmente, sarebbe un ipercono)
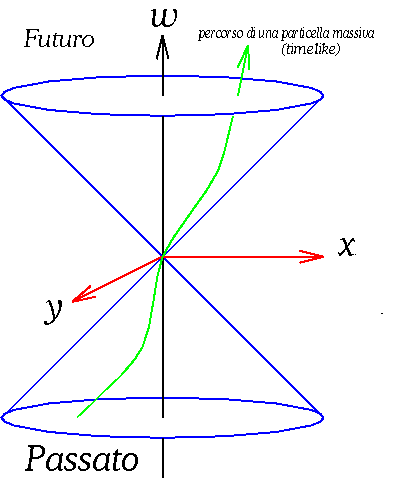
Se consideriamo uno spazio-tempo 3D (ad esempio imponendo dz=0) il cono di luce coincide con un cono geometrico, come Ŕ evidente dal seguente grafico.
Indice Lezioni - Lezione Precedente - Lezione Seguente