Lezione 2

*L'intervallo Spazio-Temporale*

di Michele Moroni

Versione 3.1 Gennaio 2003

Consideriamo un sistema di riferimento O, due eventi A [t_a,x_a,y_a,z_a,] e B[t_b,x_b,y_b,z_b] e infine la grandezza definita dalla relazione

(1)

è chiamato INTERVALLO SPAZIOTEMPORALE

Teorema 1: L'intervallo spazio-temporale tra due eventi è costante in ogni sistema di riferimento inerziale

Dimostrazione

Consideriamo un sistema di riferimento O' che si muove con velocità v rispetto ad O. Non si perde di generalità supponendo che v sia diretto lungo x nello spazio (x,y,z) di O In O' le coordinate degli eventi A e B sono A=[t'a,x'a,y'a,z'a] B=[t'b,x'b,y'b,z'b] , e l'espressione del è   (2) La trasformazione che lega le coordinate di un evento C nei due sistemi di riferimento è:   (3) Combinando la (3) e la (2) si ricava... Sviluppando i quadrati, eliminando i termini comuni e semplificando Ovvero quindi, per confronto con l'equazione 1 il teorema è dimostrato

Spesso l'invarianza dell'intervallo spazio-temporale è espressa dicendo che questa grandezza è "Lorentz invariante"

Se gli eventi A e B sono situati uno molto vicino all'altro (i matematici dicono a "distanza infinitesima") si preferisce parlare di "intervallo spazio temporale elementare e indicarlo come

*Lo Spazio Minkowskiano*

Introducendo la trasformazione di coordinate (t,x,y,z)-->(it, x,y,z), e tenendo conto che

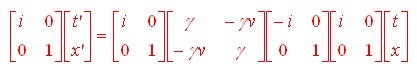
è possibile scrivere la trasformazione di Lorentz come:

(4)

con

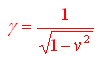
Osserviamo immediatamente che la grandezza v² e' sempre compresa tra 0 e 1; e' quindi possibile effettuare la sostituzione

v = tanh f

dove è un parametro reale

Ricordando che cosh²x- sinh²x =1 si dimostra in maniera elementare che la relazione (2) può essere scritta come

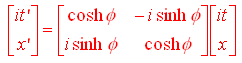
Introduciamo dunque la nuova variabile (complessa)
la precedente relazione viene riscritta come

tenendo conto delle definizioni elementari.

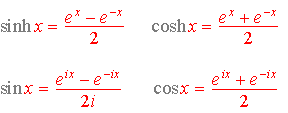
si ricava

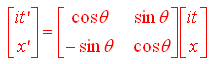
Osserviamo quindi che la matrice che lega i vettori [it', x'] e [it, x] è una matrice di rotazione con angolo complesso

Risulta quindi comodo introdurre uno spazio vettoriale complesso (SPAZIO MINKOWSKIANO) avente vettori di base [iw₀,x₀] e considerare la trasformazione tra i sistemi di riferimento di O' e O come una rotazione in questo spazio vettoriale (con angolo di rotazione a sua volta complesso)

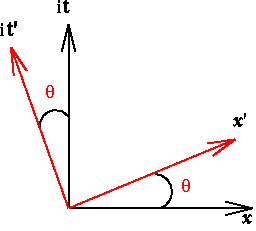
E' evidente che l'intervallo spazio-temporale nello Spazio Minkowskiano assume la forma

e quindi può essere interpretato come il modulo quadro di un vettore.

Indice Lezioni - Lezione Precedente - Lezione Seguente