Lezione 24

*Il redshift gravitazionale*

di Michele Moroni

Per introdurre il redshift gravitazionale consideriamo un esperimento ideale.

Prendiamo un campo gravitazionale uniforme, ovvero un campo gravitazionale in cui, per definizione, il (trivettore) forza che agisce su un corpo di massa m è uniforme in tutto lo spazio.

Lasciamo quindi cadere questo corpo da una posizione generica all'interno del campo. Ovviamente è verificata la relazione

1)

dove F è la componente spaziale della quadriforza e a la componente spaziale della quadriaccelerazione

In accordo con quello visto nella lezione 12

avendo v la stessa direzione di dv/dt la precedente relazione si semplifica in

Da cui, sostituendo nella 1)

Nell'istante t₀ in cui il corpo inizia a cadere risulta

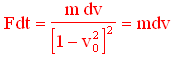2)

Prima della caduta il corpo aveva ovviamente una energia data da

E = m

Dopo l'intervallo di tempo infinitesimo dt il corpo avrà una energia data da

(nell'ultimo passaggio abbiamo effettuato uno sviluppo di Taylor e come usuale per grandeze infinitesime ci siamo fermati al primo ordine)

Ammettiamo che, nel nostro esperimento ideale, il corpo di massa m possa a questo punto essere convertito in un fotone e rispedito nella posizione iniziale. Immaginiamo poi che, una volta raggiunta la posizione iniziale, il fotone sia riconvertito in un corpo materiale. Se il fotone non perdesse energia durante la risalita sarebbe possibile guadagnare energia a spese del campo gravitazionale... ma il campo gravitazionale non viene modificato dall'esperimento, quindi questo contraddice il principio di conservazione dell'energia.

Per ovviare a questo problema, quando il fotone scala il campo gravitazionale deve per forza perdere energia in modo da riequilibrare il bilancio energetico, e arrivare al punto di partenza con una energia E corrispondente a m.

Risulta quindi che, se indichiamo con Ee l'energia che il fotone ha nel punto in cui parte e Eo quella che ha nel punto in cui arriva (riscalando il campo gravitazionale per una distanza infinitesima) deve essere

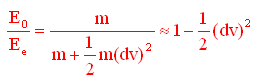
(come al solito nell'ultimo passaggio abbiamo effettuato uno sviluppo di Taylor, lecito per dv infinitesimo)

Da questa, utilizzando la relazione 2)

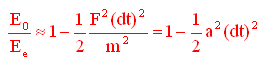
Ma, come è banalmente dimostrabile dalla teoria del calcolo infinitesimale (non ci soffermeremo qui piu' a lungo in quanto non è la sede adatta)

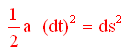
e quindi

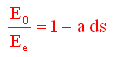
Ma dato che E₀-E_e = dE dopo qualche semplice passaggio la precedente può essere scritta come

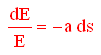
Sapendo che la frequenza di un fotone è direttamente proporzionale alla sua energia, secondo la relazione di plank E=h_rv

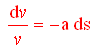
[espressione canonica del redshif gravitazionale in unità relativistiche]

Aggiungiamo che il redshift gravitazionale è stato misurato sperimentalmente in molti casi e i risultati ben si accordano alla formula generale sopra ricavata. Come caso specifico possiamo citiare ad esempio l'esperimento di Pound e Rebka del 1965, dove il RG è stato misurato utilizzando genialmente l'effetto Mossbauer (vedi Misner, Thorne, and Wheeler, Gravitation, 1970)

Indice Lezioni - Lezione Precedente - Lezione Seguente