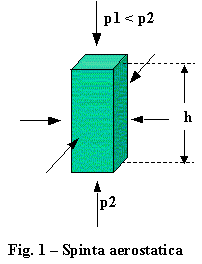
Se consideriamo un corpo immerso in un fluido in quiete, come quello di figura 1, notiamo che le forze generate dalle pressioni laterali si annullano a vicenda e non hanno effetti sul corpo. La pressione che si esercita sulla base inferiore invece, è più alta di quella che si esercita sulla base superiore, perchè la pressione varia con l'altezza all'interno del fluido. La differenza di pressione è data da h r g, dove h è l'altezza del corpo r è la densità del fluido e g è l'accelerazione di gravità. Se le basi hanno superfice S, allora la forza totale che agisce sul corpo è data da F = S h r g verso l'alto. Questo però è il volume del corpo, moltiplicato per la forza peso del fluido. Questo è il famoso principio di Archimede, che è facilmente avvertibile in acqua e che fa volare mongolfiere e dirigibili in aria. Nel caso di aerei di ogni tipo, però, i suoi effetti sono del tutto trascurabili e noi possiamo supporre che in queste condizioni l'unica forza applicata al corpo sia il suo peso.Se invece il fluido intorno al corpo è in movimento, allora le cose cambiano decisamente. La situazione viene illustrata in figura 2, dove si suppone un corpo di forma qualsiasi immerso in un fluido in movimento. La figura indica le forze aerodinamiche e non la forza peso, che supponiamo compensata in qualche modo (corpo appeso o appoggiato).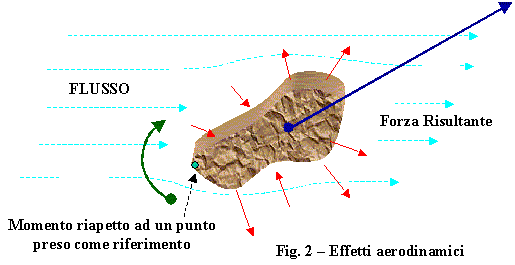 
Come si è visto in precedenza, a causa dell'infittirsi o diradarsi delle linee di flusso nei pressi di ogni elemento di superficie, la pressione del fluido varia da punto a punto e quindi variano le forze che questa pressione applica ai vari punti della superficie. La forza risultante (trascurata la spinta statica, molto più piccola) ha sempre una componente nella direzione del flusso, ma anche una componente variamente orientata nel piano perpendicolare al flusso. Inoltre, la forza risultante dipende dalla forma della superficie, e quindi, di norma, non è applicata al baricentro del corpo. Esiste allora anche un momento che tende a far ruotare il corpo. Questo momento, nelle misure, viene riferito ad un dato punto del corpo, come si vedrà nel seguito. Per sfruttare gli effetti delle forze aerodinamiche occorre dare al corpo una sagoma opportuna e mantenerlo in posizione opportuna rispetto alla velocità del fluido. È ovvio che questa forma sarà quella di un'ala, ma procediamo con calma. La figura 3 illustra i termini del problema. Il corpo è appunto sagomato come un'ala. È un solido con due basi uguali verticali aventi forma di profilo alare, chiuso da una superfice a generatrici parallele tra loro e perpendicolari alle basi. Chiamiamo estradosso la parte superiore di questa superfice, ed intradosso la parte inferiore. La generatrice anteriore rispetto al flusso, comune ad intradosso ed estradosso viene chiamata Bordo di Attacco, quella posteriore viene chiamata Bordo di Uscita. intendiamo come Corde Alari i segmenti perpendicolari ai due bordi perpendicolare ai due bordi che li uniscono. Parlando di Superfice dell'ala intendiamo la superfice della proiezione dell'ala su di un piano parallelo alle corde, o, nel nostro caso, la porzione di piano che contiene tutte le corde. 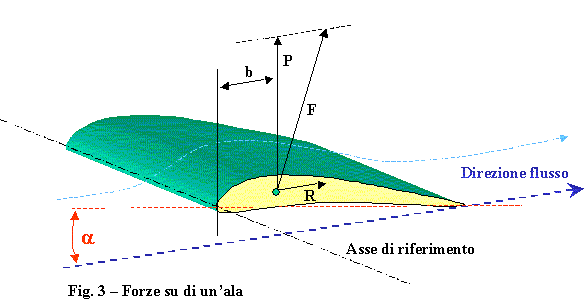 Infine immergiamo il tutto in un flusso d'aria avente velocità costante nei vari punti con una direzione che forma un angolo a con le corde. Il flusso sia perpendicolare alle generatrici di intradosso ed estradosso. Passiamo quindi ad esaminare la figura 3, che illustra la situazione descritta e che cosa succede. Poiché i punti di applicazione delle forze sono al momento ignoti, assumiamo come asse di riferimento la linea che contiene il bordo di attacco. Si sviluppa una forza F, risultante di tutte le forze aerodinamiche, applicata in un punto (per semplicità rappresentato sulla faccia di profilo, in realtà interno), che può essere scomposta in una componente P normale al flusso ed in una componente R parallela al flusso. Rispetto al bordo di attacco questa forza ha un dato braccio b e quindi un dato momento M. Se il braccio è misurato come in figura, il momento risulta essere pari a M = b P. Si nota che: 1) - La forza dipende dal particolare profilo sperimentato 2) - La forza dipende dall'angolo di incidenza a 3) - La forza dipende dalla Superfice del campione sperimentato in modo lineare 4) - La forza dipende dalla velocità del flusso in modo quadratico 5) - La forza dipende dalla densità del fluido in modo lineare Queste dipendenze sono ovviamente valide per le due componenti della forza, P (o portanza) ed R (o resistenza). Le relazioni con l'angolo di incidenza e con il profilo (supposto che questo sia matematicamente descrivibile, sono estremamente complesse e pertanto vengono determinate sperimentalmente. A questo punto possono essere scritte le dipendenze di cui sopra nella forma: P = Cp r S v² ; R = Cr r S v² dove Cp e Cr, rispettivamente coefficienti di portanza e resistenza, devono essere determinati sperimentalmente per ogni profilo ed ogni angolo di incidenza. Allo stesso modo si può stabilire un coefficiente di Momento. Dalla figura risulterebbe che il momento è dato dalla portanza per il braccio vero rispetto al bordo di attacco. Si preferisce utilizzare un braccio convenzionale. Poichè il coefficiente viene misurato sperimentalmente, si può assumere un braccio convenzionale e riferire il momento a quel braccio. Tenendo poi presente questa convenzione, i conti successivi continueranno a tornare. Naturalmente il coefficiente Cm per il momento diventa diverso da quello per la portanza. Come braccio convenzionale si assume la corda alare l o la corda media se questa non è costante. Anche per il momento M, allora si può scrivere: M=Cm r S v² l Per potere utilizzare queste espressioni occorre disporre, per un dato profilo alare, dei valori di questi coefficienti per ciascuno degli angoli di incidenza ai quali potrà operare l'ala (le curve dei coefficienti in funzione dell'angolo di incidenza). 
L'apparecchiatura che serve allo scopo è la galleria del vento, di cui è data una rappresentazione schematica nella figura non numerata a fianco.In un condotto opportunamente sagomato una ventola mette in moto l'aria. Nel condotto vi è un "volume utile"accessibile dall'esterno, nel quale il flusso d'aria ha le caratteristiche di parallelismo e velocità costante richieste dalle misure. La velocità viene misurata in vari punti per verifica da tubi di Pitòt che ne danno un valore preciso. in questo volume è messo il modello in esame, trattenuto da sottili fili inestensibili attraverso i quali è possibile assicurare precisamente la posizione del modello e misurare le forze che si sviluppano. Nelle misue sono compensati tanto il peso del modello quanto le azioni aerodinamiche sui fili. Dalle forze misurate si calcolano le azioni aerodinamiche e quindi, dalle dimensioni del modello e dalla velocità nota, si derivano i coefficienti cercati. La prova viene ripetuta per tutti gli angoli di incidenza di interesse. In questo modo è possibile ottenere le tabelle o curve dei coefficienti in funzione dell'incidenza per quel particolare profilo alare. Vi sono comunque due punti su cui occorre richiamare l'attenzione. 1) - La prova avviene ad un certo Numero di Reynol (di cui si è detto). I coefficienti trovati sono applicabili ad ogni situazione reale per la quale il numero di Reynold non sia troppo diverso da quello della misura. Variando la velocità si può vedere cosa succede al variare del numero di Reynold, ma i dati non possono essere troppo "estrapolati" in quanto potrebbero esserci variazioni imprevedibili e veloci al di fuori del campo di misure effettuate.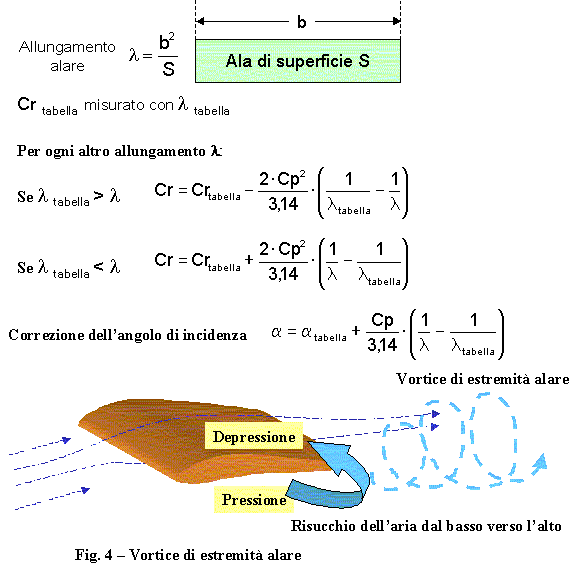 
2) - Il secondo punto si riferisce alla "Resistenza Indotta" di cui parliamo un po' più diffusamente. La figura 4 illustra di che cosa si tratta. Sull'estradosso dell'ala si genera una depressione, mentre sull'intradosso la pressione sale. Comunque, in ogni caso in cui la portanza non è nulla, esiste una differenza di pressione tra le due superfici dell'ala. Questo, all'estremità dell'ala provoca un risucchio d'aria che genera un vortice. Questo vortice "induce"una resistenza aggiuntiva. Questa resistenza è tanto più grossa quanto più è piccolo il rapporto tra l'aperura dell'ala e la sua superficie. Ali tozze sono più resistenti all'aria di ali slanciate (vedasi le ali dei veleggiatori). Il rapporto l tra il quadrato dell'apertura e la superficie dell'ala si chiama "Allungamento". In galleria del vento, le misure sono effettuate su modelli di dato allungamento. e per utilizzare questi dati su ali di allungamento diverso, occorre effettuare una correzione, come indicato in figura. L'effetto del vortice è infatti calcolabile.Il calcolo implica che venga anche corretto l'angolo a cui la misura si riferisce. La relativa formula è riportata in figura. Questo significa che per allungamenti diversi da quelli tabellari di misura, le curve dei coefficienti relativi ad un dato profilo vengono "ridisegnate" secondo le espressioni riportate. L'allungamento del modello misurato, assieme al numero di Reynold della misura, sono quindi due grandezze, parametri della misura, che devono essere riportate assieme ai risultati. I risultati delle misure fatte nella galleria del vento vengono riportati su tabelle e diagrammi di tre tipi. 1) - Diagrammi riferiti all'angolo a di incidenza. Su questi diagrammi in ascisse si riporta l'angolo ed in ordinate il parametro che interessa. Su questo tipo di diagramma si dà anche (in ordinate) il rapporto, per ogni angolo, tra Cp e Cr, che viene detto "Efficienza" del profilo e si indica con E. 2) - Diagrammi polari per i quali in ascisse si riportano i coefficienti di resistenza Cr ed in ordinate quelli di portanza Cp. Sulla curva risultante sono indicati gli angoli a cui i punti corrispondono. 3) - Diagrammi riferiti ai momenti, simili ai diagrammi polari, dove però anziché la resistenza, in ascisse vengono riportati i coefficienti di momento Cm. Questi diagrammi sono particolarmente preziosi per la soluzione grafica dei problemi di stabilità, come si vedrà. 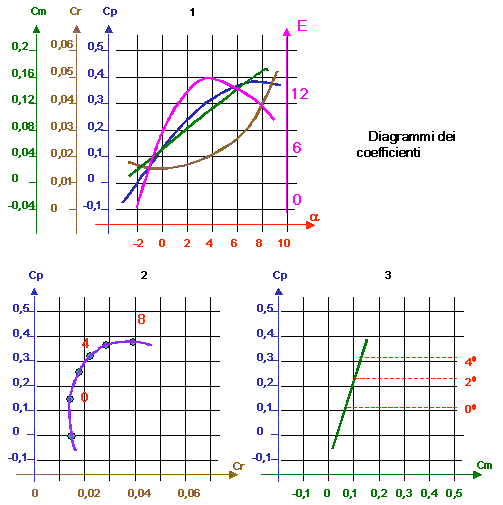 La figura non numerata qui a fianco riporta questi diagrammi. Si nota come le incidenze utili per le quali l'ala sviluppa una buona portanza e bassa resistenza, si trovano in un campo piuttosto limitato. Al di sopra di incidenze che a seconda dei profili vanno approssimativamente da 10 a 15 gradi, la portanza si riduce bruscamente, mentre la resistenza tende ad un forte aumento. Queste sono le condizioni di "stallo", limite al quale l'ala smette di fare il suo mestiere. Un'altra cosa importante che si osserva ui diagrammi, è che per le incidenze utili (piccoli angoli) il diagramma della portanza in funzione del momento è praticamente un segmento di retta. Questo fatto, sistematico per ogni profilo, semplifica molto la vita nel calcolo delle condizioni di stabilità. Di fatto rende possibile un metodo grafico non eccessivamente complesso. Infine si nota come la massima efficienza di un profilo si ottiene ad un dato angolo di incidenza. È allora ragionevole pensare che se il profilo lavorerà a quell'angolo il velivolo avrà un migliore comportamento. Si vedrà nel seguito come cercare di ottenere quiesto risultato. Finora ci siamo occupati dei coefficienti aerodinamici relarivi alle ali, che valgono ovviamente anche per le superfici quali timone e stabilizzatori, ma questi elementi non volano da soli. Un'altro punto importante è il comportamento aerodinamico della fusoliera. Come ogni altro elemento immerso nel flusso d'aria, anche la fusoliera ha una Portanza, una Resistenza, un Momento che saranno funzione del suo angolo di incidenza, del numero di Reynold e della sua sagoma. Con le stesse regole precedenti, il suo comportamento può essere misurato nella galleria del vento. Sebbene non sia sempre così, qui facciamo l'assunzione approssimativa che l'unico elemento significativo sia la resistenza che la fusoliera sviluppa, mentre portanza e momenti non vengono modificati dalla sua presenza. 
Il criterio generale dovrebbe esser che il coefficiente di resistenza della fusoliera viene riferito alla sezione maestra, dipende dalla forma della fusoliera e dal suo angolo di incidenza rispetto al flusso. Come per la fusoliera, tutti gli altri elementi esposti al vento, come motori applicati all'ala, carrelli etc., sviluppano una resistenza. L'espressione generale è ancora quella di ogni resitenza aerodinamica e cioè una dipendenza lineare dalla densità del fluido e dalla sezione maestra, ed una dipendenza quadratica dalla velocità. Il riferimento alla sezione maestra (la massima sezione ortogonale al moto) di corpi fusiformi, produce coefficienti molto più grandi di quelli trovati per le ali, in quanto la sezione a cui si riferiscono è proporzionalmente molto più piccola. La figura 5 completa il discorso..Può essere aggiunto che il valore di resistenza della fusoliera è molto variabile con il numero di Reynold , e contemporaneamente non varia molto con l'angolo di incidenza. Valori misurati a numeri di Reynold alti vanno tra 0,05 e 0,2 ma questi sono valori che tendono a crescere anche di molto al diminuire del numero di Reynold. Nel caso di piccoli modelli a bassa velocità questo coefficiente potrebbe essere considerato tra 0,5 e 0,8 approssimativamente. |
Il Palazzo Carignano a Torino.
