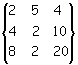
Il calcolo della matrice inversa.

Problema. Ricavare la matrice inversa della matrice

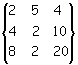
Per la risoluzione del problema verrà usato il metodo di Jordan (Camille, 1838-1922, matematico francese), basato sulla elaborazione delle singole righe. In pratica ogni riga verrà opportunamente trasformata dividendola per un coefficiente o combinandola linearmente con un'altra.

Si affianca, preliminarmente, alla matrice in esame la matrice identità

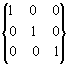
componendo l'unica matrice

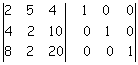
Primo passaggio.

Si vogliono trasformare le righe in modo che la prima colonna diventi

Per ottenere lo scopo, si divide dapprima per 2 la prima riga, ottenendo

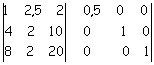
Si moltiplica ora per -4 la prima riga

e la si aggiunge alla seconda

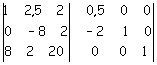
Si moltiplica, infine, per -8 la prima riga

e la si aggiunge alla terza

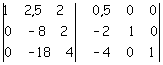
Secondo passaggio.

Si vogliono trasformare le righe in modo che la seconda colonna diventi

Per ottenere lo scopo, si divide dapprima per -8 la seconda riga, ottenendo

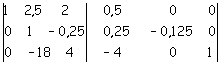
Si moltiplica ora per -2,5 la seconda riga

e la si somma alla prima

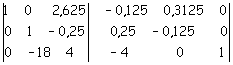
Si moltiplica,infine, per +18 la seconda riga

e la si somma alla terza

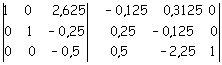
Terzo passaggio.

Analogamente, si vogliono trasformare le righe in modo che la terza colonna diventi

Utilizzando la tecnica già esaminata, si divide per -0,5 la terza riga

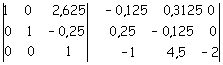
Si moltiplica per -2,625 la terza riga

e la si somma alla prima

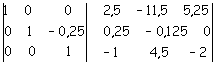
Si moltiplica,infine, per +0,25 la terza riga

e la si somma alla seconda

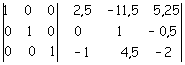
La parte sinistra della matrice è ora diventata la matrice identità; la parte destra è la matrice inversa ricercata.

In definitiva la matrice inversa è

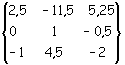
Il calcolo, come si è potuto constatare, è abbastanza complesso. Le difficoltà possono essere superate agevolmente con l’impiego del foglio elettronico di calcolo Excel, il quale dispone della funzione =MATR.INVERSA(matrice) che risolve il problema immediatamente.