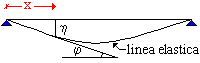Le deformazioni

Le deformazioni.
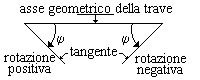
La linea elastica. La rotazione di due sezioni parallele di un concio di trave. . La convenzione di segno per le rotazioni.		La linea elastica. Sotto l'azione dei carichi esterni l'asse geometrico della trave assume una nuova configurazione denominata linea elastica. Più in particolare: il singolo punto subisce uno spostamento h; due sezioni vicine, originariamente parallele, si inclinano e diventano convergenti. L'angolo di rotazione j che esse vengono a formare è uguale a quello formato dalla tangente alla linea elastica e dalla linea orizzontale. In generale, fissato un sistema di riferimento, lo spostamento h e la rotazione j variano con l'ascissa x. Sono considerati positivi gli spostamenti verso il basso, gli abbassamenti, e le rotazioni orarie che l'asse geometrico della trave deve effettuare per sovrapporsi alla tangente alla linea elastica.
Il calcolo delle deformazioni. Vi sono diversi metodi che possono essere impiegati per calcolare le deformazioni di una trave; quello indicato da Mohr (Christian Otto, 1835-1918) presenta il vantaggio di utilizzare le tecniche, già note, usate per il tracciamento dei diagrammi delle sollecitazioni. Per il teorema di Mohr, infatti, gli abbassamenti di una trave, la trave reale, sono equivalenti ai valori dei momenti M^* di una seconda trave, la trave ausiliaria, il cui carico è costituito dal diagramma dei momenti della trave reale. I valori vanno divisi per il prodotto EI, dove E è il modulo elastico del materiale ed I è il momento di inerzia baricentrico della sezione della trave. I due corollari del teorema di Mohr consentono il calcolo delle rotazioni. 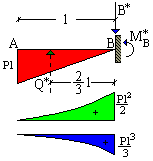Si ha, infatti, che: le rotazioni delle sezioni sono pari ai valori del taglio T^* della trave ausiliaria divisi per EI. le rotazioni a e b delle sezioni terminali sono uguali, in valore assoluto, ai valori delle reazioni A^* e B^* della trave ausiliaria divisi per EI.
La trave ausiliaria. La trave ausiliaria corrispondente ad una trave reale semplicemente appoggiata è ancora una trave semplicemente appoggiata. La trave ausiliaria corrispondente ad una trave reale a sbalzo è ancora una trave a sbalzo ma presenta il vincolo d'incastro nell'estremo opposto. Il carico della trave ausiliaria è rappresentato dal diagramma dei momenti della trave reale ribaltato rispetto all'asse orizzontale.
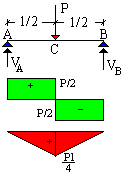
La trave semplicemente appoggiata, con una forza in mezzeria.	La trave reale.		La trave ausiliaria. Il diagramma dei momenti, letto nella scala 1:EI, rappresenta la linea elastica della trave reale.
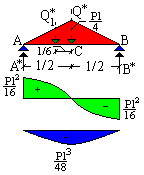
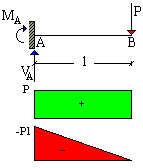La trave incastrata. con una forza sull'estremo libero.	La trave reale.		La trave ausiliaria. Si noti la posizione dell'incastro sull'estremo opposto.
Finalità del calcolo delle deformazioni. Un primo scopo che si può raggiungere con il calcolo delle deformazioni è la verifica delle condizioni di esercizio delle strutture: una trave, ad esempio, pur se funzionale dal punto di vista delle tensioni, potrebbe non essere utilizzabile a causa della sua eccessiva deformabilità. Una seconda possibilità, non meno importante della prima, offerta dal calcolo delle deformazioni è la ricerca delle incognite iperstatiche: quando non sono sufficienti le equazioni della statica alla determinazione delle reazioni vincolari di una struttura, si aggiungono ulteriori equazioni di congruenza delle deformazioni per calcolare il valore delle incognite sovrabbondanti.