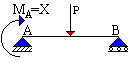Il metodo delle rotazioni e quello degli spostamenti

Il metodo delle rotazioni e quello degli spostamenti.
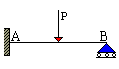
La trave in figura possiede un grado di iperstaticità.	Il calcolo delle incognite iperstatiche. La trave in figura ha tre gradi di libertà e quattro limitazioni vincolari, tre delle quali offerte dall'incastro ed una dal carrello: si tratta perciò di una struttura caratterizzata da un grado di iperstaticità. La scrittura delle tre equazioni cardinali della statica non è sufficiente alla determinazione delle quattro reazioni vincolari: occorre aggiungere una quarta equazione. A tal fine si scrive un'equazione che imponga il rispetto della congruenza delle deformazioni. In altri termini si può aggiungere un'equazione che tenga conto del fatto che il punto B non può spostarsi (metodo degli abbassamenti) o che, nell'estremo vincolato dall'incastro, la rotazione sia nulla (metodo delle rotazioni).
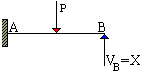
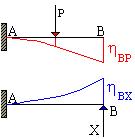
Il metodo degli spostamenti.	Il metodo degli spostamenti. Se si assume quale incognita iperstatica la reazione V_B, esistono infiniti valori X che consentono l'equilibrio della trave. Di essi, però, uno solo è tale da garantire lo spostamento nullo per il punto B. Se h_BP è l'abbassamento, positivo, provocato dal carico P agente sulla trave e h_BX l'innalzamento, negativo, prodotto dalla reazione iperstatica X si deve avere h_BP + h_BX = 0 poiché lo spostamento totale h_B è nullo per la presenza del carrello. Nell'equazione h_BP è noto mentre h_BX contiene l'incognita X che può così essere determinata.
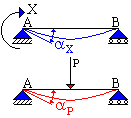
Il metodo delle rotazioni.	Il metodo delle rotazioni. L'incastro può essere trasformato in una cerniera con l'aggiunta di un momento M_A. Se si assume quale incognita iperstatica proprio tale momento, esistono infiniti valori X che consentono l'equilibrio della trave. Di essi, però, uno solo è tale da garantire che la rotazione nella sezione A, vincolata dall'incastro, sia nulla. Il carico P agente sulla trave provoca una rotazione a_P mentre il momento X produce una rotazione a_X. La sommatoria delle due rotazioni deve risultare nulla a_P + a_X = 0 perché, come si è detto è a = 0 a causa della presenza dell'incastro. Nell'equazione a_P è noto mentre a_X contiene l'incognita X che può in tal modo essere calcolata.
Il calcolo delle deformazioni. Per calcolare gli spostamenti e le rotazioni da introdurre nelle due equazioni precedenti si possono tracciare i diagrammi delle sollecitazioni della trave ausiliaria, in accordo con il teorema di Mohr e i suoi due corollari. Nel confronto tra i due metodi, è da rimarcare che per individuare il valore delle rotazioni è sufficiente calcolare le reazioni della trave ausiliaria mentre per determinare gli abbassamenti è necessario il tracciamento, spesso abbastanza complesso, del diagramma dei momenti di tale trave; è evidente allora come il metodo delle rotazioni risulti di gran lunga di più facile impiego. Per tale metodo risultano, inoltre, disponibili nella formulistica corrente i valori delle rotazioni relative ad un numero rilevante di travi appoggiate.