Analisi
plastica. Trave Incastro-Appoggio.
Carico uniformemente distribuito.
Problema. Dopo aver determinato la posizione della cerniera
plastica di campata per la trave in figura calcolare il valore del carico limite
ql utilizzando rispettivamente il metodo statico e quello cinematico.
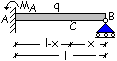
Reazioni e diagramma dei momenti
La reazione
elastica MA offerta dall’incastro vale
Essa ha un valore
negativo nel diagramma dei momenti.
Formazione delle cerniere
plastiche
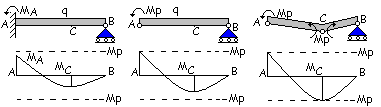
Al
crescere del carico q il momento MA aumenta fino a raggiungere il
valore del momento plastico Mp. L’incastro in A si trasforma in
cerniera plastica in corrispondenza della quale è applicato il momento Mp.
Aumentando
ancora il carico q fino al valore del carico limite ql, il momento MC
cresce fino a raggiungere anch’esso un valore pari a Mp. L’incastro
interno in C si trasforma in una cerniera plastica in corrispondenza della
quale è applicato ancora il momento Mp. La struttura assume la forma
di un cinematismo ed un qualsiasi ulteriore aumento del carico ql ne
procura il movimento.
Soluzione statica (metodo lower
bound: metodo del limite inferiore)
Il
carico limite calcolato con il metodo statico conduce ad un carico limite ql
minore o al limite uguale all’effettivo carico limite. L’impiego del metodo è preferibile
per strutture composte da pochi elementi come quella in esame.
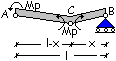
Come
primo passaggio occorre determinare la posizione incognita della cerniera
plastica.
Per
l’equilibrio verticale del tratto CB si ha
|
|
La
reazione verticale in C è nulla perché nel punto C si ha il massimo momento
ed il taglio è nullo. |
Considerando
l’equilibrio alla rotazione in C del tratto CB si ha
Considerando,
infine, l’equilibrio alla rotazione in A
del tratto AB si ha
In
definitiva è
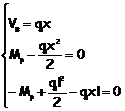
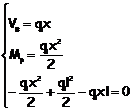
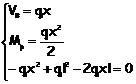
L’ultima
equazione diventa
L’unica
soluzione positiva è
E’
ora possibile determinare il valore del carico limite.
Dalla
seconda equazione del sistema si ha
Soluzione cinematica (metodo
upper bound: metodo del limite superiore).
Il
carico limite calcolato con il metodo cinematico conduce ad un carico limite ql
maggiore o al limite uguale all’effettivo carico limite.
Esso
è basato sul teorema dei lavori virtuali secondo il quale, al momento della
formazione della cerniera in C, il lavoro prodotto dalle forze reali esterne
(il carico ql) dovrà uguagliare quello delle forze interne (i
momenti Mp in A e i due momenti Mp in C).
Nell’esempio
si seguirà la seconda modalità di applicazione del teorema, assegnando al
sistema delle forze equilibrate (
,
e i tre momenti Mp) un sistema di spostamenti
arbitrari ma congruente (gli abbassamenti wA, wB e gli
angoli a e b).
|
|
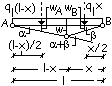
Il
teorema dei lavori virtuali può essere applicato con quattro differenti
modalità:
Le
forze producono spostamenti: il lavoro è dato dal prodotto della loro
intensità per lo spostamento. I
momenti producono rotazioni: il lavoro è dato dal prodotto della coppia per
la rotazione (espressa in radianti). |
All’abbassamento
del punto C della quantità w corrispondono le rotazioni congruenti a e
b.
Per
angoli molto piccoli la tangente può confondersi con il valore dell’angolo
espresso in radianti.
Si
ha
Gli abbassamenti in corrispondenza delle
risultanti dei due carichi distribuiti valgono rispettivamente:
Il lavoro esterno
è dato da
Il lavoro interno
è dato da
Nella quale il
secondo addendo esprime la somma dei lavori prodotti nel tratto AC (Mpa)
e nel tratto CB (Mpb).
La posizione della
cerniera plastica può essere ottenuta ricercando il valore minimo di ql
uguagliando a zero il valore della sua derivata.
|
|
La derivata del
rapporto di funzioni
è data da
|
L’unica
soluzione positiva è
E’
ora possibile determinare il valore del carico limite.
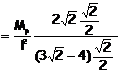
Risolvendo
rispetto al momento plastico si ottiene
