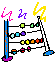 Analisi
plastica. Metodo statico (lower bound).
Analisi
plastica. Metodo statico (lower bound).
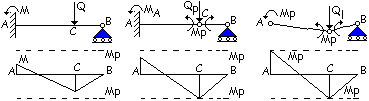
Problema. Determinare il carico limite Ql per il profilo
in acciaio in figura utilizzando il teorema del limite inferiore (metodo lower bound).
Noti: IPE 180; acciaio S235; l = 4 m; b = 2,5 m.
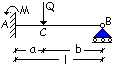
Secondo
il teorema del limite inferiore (Melan) un insieme di carichi staticamente
ammissibile per i quali non sia superato il momento plastico sopportabile da
una struttura è minore o al limite
uguale all’effettivo carico limite.
Poiché
il carico limite determinato con il metodo statico è anche minore o al limite
uguale a quello calcolato con il metodo cinematico originato dal teorema del
limite superiore (metodo upper bound) ne consegue che se l’insieme dei carichi
staticamente ammissibile dà origine anche ad un meccanismo esso corrisponde al
carico limite.
In
altri termini l’insieme dei carichi per essere considerato carico limite deve:
ü essere staticamente determinato (rispettare
cioè le equazioni della statica);
ü non deve superare le resistenze plastiche
della struttura;
ü deve originare un meccanismo.
Nel
seguito, a fini didattici, verranno esplorate diverse soluzioni staticamente
determinate per verificare praticamente il teorema, arrivando in conclusione
alla determinazione del carico limite.
Calcolo del momento plastico Mp
sopportabile dalla struttura.
La tensione di
calcolo del materiale a flessione vale
![]()
![]()
Dal
sagomario si
ricava per il profilo IPE 180
Wpl = 166415
mm3; Classe 1.
|
|
Il
profilo è in classe 1 ed è pertanto utilizzabile il calcolo plastico secondo
le Norme Tecniche. |
Il momento
plastico sopportabile dalla struttura è dato da:
![]()
![]()
|
|
Nel
calcolo precedente il taglio è stato ipotizzato trascurabile; nel caso opposto
il momento plastico subisce una riduzione del suo valore. |
Calcolo elastico
Come primo
tentativo è possibile ipotizzare, in maniera assolutamente arbitraria, un
carico Q = 38 kN in condizioni elastiche.

L’incognita
iperstatica in corrispondenza dell’incastro A vale
![]()
![]()
Essa ha un valore
negativo nel diagramma dei momenti.
Scrivendo
l’equazione di equilibrio alla rotazione in A si ottiene
![]()
![]()
![]()
Il momento di
campata vale
![]()
![]()
|
|
La
soluzione ipotizzata rispetta l’equilibrio statico, presenta la
sollecitazione massima M in A minore del momento plastico della struttura ma
è inferiore quella limite perché non dà origine ad un meccanismo. |
|
|
Il
valore di Q è stato ipotizzato in maniera arbitraria. Un valore più basso non
è di alcuno interesse poiché il carico limite è maggiore di quello
ipotizzato; valori più alti verranno ricercati nel seguito. |
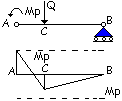
Formazione della prima cerniera
plastica.
Al
crescere del carico Q fino al raggiungimento di Qp il momento M
aumenta fino a raggiungere il valore del momento plastico Mp nella
sezione A che è quella maggiormente sollecitata. L’incastro in A si trasforma
in una cerniera plastica in corrispondenza della quale è applicato il momento Mp.
Il
carico Qp corrispondente al momento Mp vale
![]()
![]()
![]()
![]()
![]()
![]()
|
|
La
soluzione appena calcolata rispetta l’equilibrio statico, presenta la
sollecitazione massima M in A non superiore al momento plastico della
struttura ma è inferiore quella limite perché non dà origine ad un
meccanismo. |
Formazione della seconda cerniera
plastica.
Aumentando
il carico Qp, il momento MC cresce fino a raggiungere
anch’esso un valore pari a Mp. L’incastro interno in C si trasforma
in una cerniera plastica in corrispondenza della quale è applicato ancora il
momento Mp. La struttura assume la forma di un meccanismo ed un
qualsiasi ulteriore aumento del carico Q ne procura il movimento.
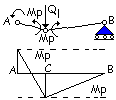
Considerando
l’equilibrio alla rotazione in C del tratto CB si ha
![]()
dalla
quale si ricava
![]()
Analogamente
l’equilibrio alla rotazione per il punto A dell’intera trave AB fornisce
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
La
soluzione appena calcolata rispetta l’equilibrio statico, presenta i momenti
massimi in A e in C non superiori al
momento plastico della struttura e corrisponde a quella limite perché dà origine ad un meccanismo. |
Verifica della soluzione.
La
soluzione calcolata in precedenza rappresenta il carico massimo sopportabile
dalla sezione. A riprova attribuiamo in maniera arbitraria un nuovo valore al
carico Q = 68kN > Ql, dopo la formazione della prima cerniera
elastica in A.
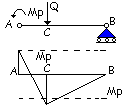
![]()
![]()
![]()
![]()
|
|
La
soluzione appena calcolata rispetta l’equilibrio statico ma presenta la
sollecitazione massima MC superiore al momento plastico della
struttura e, pertanto, non è ammissibile. |
Riepilogo.
Riassumendo
i risultati finora determinati si ottiene il seguente quadro
|
Q [kN] |
soluzione staticamente determinata |
soluzione plasticamente ammissibile |
formazione di un meccanismo |
|
38 |
si |
si |
no |
|
48,90 |
si |
si |
no |
|
64,57 |
si |
si |
si |
|
68 |
si |
no |
si |
|
|
La
formazione della prima cerniera è avvenuta nella sezione A perché il momento
elastico MA è risultato maggiore del momento MC. Nel
caso opposto il procedimento non perde la sua validità, comportando
solo un cambio di sequenza nella formazione delle cerniere (prima in C e poi
in A). La determinazione del carico limite Ql
non è influenzata dalla modalità di creazione del meccanismo, qui esposta a
soli fini didattici, ma solo dalla sua configurazione finale. La situazione ora ipotizzata si
verifica per un carico Q posto in prossimità dell’appoggio B. Ad esempio per b = 1,5 m il calcolo
elastico iniziale produce i seguenti risultati
|