 Analisi
plastica. Metodo cinematico (upper bound).
Analisi
plastica. Metodo cinematico (upper bound).
Problema. Determinare il carico limite Ql per il
profilo in acciaio in figura utilizzando il teorema del limite inferiore
(metodo upper bound).
Noti: IPE 180; acciaio S235; l = 3,6 m.
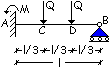
Secondo
il teorema del limite superiore (Koiter) un insieme di carichi al quale
corrisponda un meccanismo di collasso cinematicamente ammissibile è maggiore o
al limite uguale all’effettivo carico limite.
Poiché
il carico limite determinato con il metodo cinematico è anche maggiore o al
limite uguale a quello calcolato con il metodo statico originato dal teorema
del limite inferiore (lower bound) ne consegue che se l’insieme dei carichi cinematicamente
ammissibile è originato anche da una configurazione staticamente ammissibile
esso corrisponde al carico limite.
In
altri termini l’insieme dei carichi per essere considerato carico limite:
ü deve essere il minore dei carichi che
originano un meccanismo di collasso;
ü non deve superare le resistenze plastiche
della struttura;
ü essere staticamente determinato (rispettare
cioè le equazioni della statica).
Nel
seguito, a fini didattici, verranno esplorate diverse soluzioni staticamente
determinate per verificare praticamente il teorema, arrivando in conclusione
alla determinazione del carico limite.
Calcolo del momento plastico Mp
sopportabile dalla struttura.
La tensione di
calcolo del materiale a flessione vale
![]()
![]()
Dal
sagomario si
ricava per il profilo IPE 180
Wpl = 166415
mm3; Classe 1.
|
|
Il
profilo è in classe 1 ed è pertanto utilizzabile il calcolo plastico secondo
le Norme Tecniche. |
Il momento
plastico sopportabile dalla struttura è dato da:
![]()
![]()
|
|
Nel
calcolo precedente il taglio è stato ipotizzato trascurabile; nel caso
opposto il momento plastico subisce una riduzione del suo valore. |
Individuazione dei meccanismi di
collasso.
Sono ipotizzabili
tre diversi meccanismi di collasso:
ü
formazione
di due cerniere plastiche rispettivamente in A e in C
ü
formazione
di due cerniere plastiche rispettivamente in A e in D
ü
formazione
di due cerniere plastiche rispettivamente in C e in D
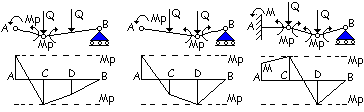
In corrispondenza
delle cerniere plastiche il momento non può superare il momento plastico della
struttura.
Il
metodo cinematico è basato sul teorema dei lavori virtuali secondo il quale, al
momento del raggiungimento del meccanismo di collasso, il lavoro prodotto dalle
forze reali esterne (i carichi Q) dovrà uguagliare quello delle forze interne (i
momenti Mp).
Nell’esempio
si seguirà la seconda modalità di applicazione del teorema, assegnando al
sistema delle forze equilibrate (Q e i momenti Mp) un sistema di
spostamenti arbitrari ma congruente (gli abbassamenti wC e wD
e gli angoli a e b).
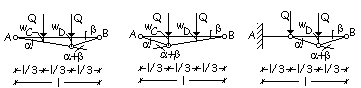
|
|
Il
teorema dei lavori virtuali può essere applicato con quattro differenti
modalità:
Le
forze producono spostamenti: il lavoro è dato dal prodotto della loro
intensità per lo spostamento. I
momenti producono rotazioni: il lavoro è dato dal prodotto della coppia per
la rotazione (espressa in radianti). Nell’ultimo
meccanismo di collasso il momento in A non produce lavoro essendo nulla la
rotazione in corrispondenza dell’incastro. |
Primo meccanismo di collasso.
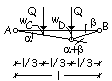
All’abbassamento
del punto D della quantità wD corrispondono le rotazioni congruenti a e
b.
Per
angoli molto piccoli la tangente può confondersi con il valore dell’angolo
espresso in radianti.
Si
ha
![]()
![]()
![]()
Il lavoro esterno
è dato da
![]()
![]()
![]()
![]()
Il lavoro interno
è dato da
![]()
Nella quale il
secondo addendo esprime la somma dei lavori prodotti nel tratto AD (Mpa)
e nel tratto DB (Mpb).
![]()
![]()
![]()
![]()
![]()
|
|
Il
carico genera un meccanismo di collasso, non supera la resistenza plastica
offerta dalla struttura, è staticamente determinato. Per
essere il carico limite deve risultare il carico minimo nel confronto con gli
altri meccanismi di collasso. |
Secondo meccanismo di collasso.
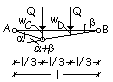
All’abbassamento
del punto C della quantità wC corrispondono le rotazioni congruenti a e
b.
Per
angoli molto piccoli la tangente può confondersi con il valore dell’angolo
espresso in radianti.
Si
ha
![]()
![]()
![]()
Il lavoro esterno
è dato da
![]()
![]()
![]()
![]()
Il lavoro interno
è dato da
![]()
Nella quale il
secondo addendo esprime la somma dei lavori prodotti nel tratto AC (Mpa)
e nel tratto CB (Mpb).
![]()
![]()
![]()
![]()
![]()
|
|
Il
carico genera un meccanismo di collasso, non supera la resistenza plastica
offerta dalla struttura, è staticamente determinato. Non
può essere considerato quale carico limite perché supera il carico ottenuto
con il primo meccanismo di collasso esaminato in precedenza. |
Terzo meccanismo di collasso.

All’abbassamento
del punto D della quantità wD corrispondono le rotazioni congruenti a e
b.
Per
angoli molto piccoli la tangente può confondersi con il valore dell’angolo
espresso in radianti.
Si
ha
![]()
![]()
![]()
Il lavoro esterno
è dato da
![]()
![]()
Il lavoro interno
è dato da
![]()
Nella quale il
secondo addendo esprime la somma dei lavori prodotti nel tratto CD (Mpa)
e nel tratto DB (Mpb).
![]()
![]()
![]()
![]()
![]()
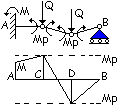
Analizzando
l’equilibrio alla rotazione in D del tratto DB si ottiene
![]()
![]()
![]()
Il
momento all’incastro vale quindi
![]()
![]()
|
|
Il
carico genera un meccanismo di collasso, è staticamente determinato ma supera
la resistenza plastica offerta dalla struttura. Non
può essere considerato quale carico limite sia perché supera il carico
ottenuto con il primo meccanismo di collasso esaminato in precedenza sia
perché supera la resistenza plastica della struttura. |
Riepilogo.
Riassumendo
i risultati finora determinati si ottiene il seguente quadro
|
Q [kN] |
soluzione staticamente determinata |
soluzione plasticamente ammissibile |
carico minore |
|
41,39 |
si |
si |
si |
|
51,74 |
si |
si |
no |
|
93,13 |
si |
no |
no |
dal quale si desume il carico limite
![]()