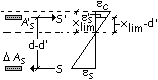Confronto analisi. Cemento armato.
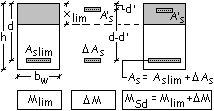
Problema. Determinare l’armatura necessaria alla
trave in spessore di solaio in figura utilizzando
a) l’analisi elastica lineare
senza ridistribuzione dei momenti;
b) l’analisi elastica lineare
con ridistribuzione dei momenti (d
= 0,8).
Determinare inoltre:
ü
il
momento di fessurazione Mcr per il caso a);
ü
il
carico massimo variabile sopportabile dalla struttura utilizzando l’analisi
plastica per il caso b).
Noti: b = 45 cm; h =22 cm; l = 4,5 m; q = 12,60
kN/m; calcestruzzo C25/30 (Rck = 30 N/mm2); acciaio
B450C; classe di esposizione XC1 (calcestruzzo all'interno di edifici con bassa
umidità relativa.); fmin =
I
valori di calcolo dei due materiali risultano pari rispettivamente a:
acciaio: fyd =
391 N/mm2 fyk = 450 N/mm2; 
calcestruzzo fcd =
14,11 N/mm2; fctm = 2,56 N/mm2; 
La
percentuale minima di armatura vale:
Il
copriferro minimo è pari a cmin =
Assunta
una tolleranza di esecuzione Dcdev =
Cnom = 15 + 10
=
La
distanza reciproca tra le barre (interferro) deve risultare almeno pari a
ifmin = Dmax
+ 5 = 25 + 5 =
Il carico
permanente strutturale vale
Analisi elastica lineare senza
ridistribuzione dei momenti.
Per
il calcolo del momento sull’appoggio centrale la configurazione di carico è
costituita dal carico g1 ed il carico q presenti su entrambe le
campate.
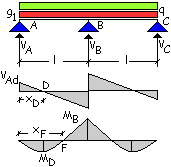
Si ha
Applicando
la formula di correlazione agli SLU, è
Con
la stessa configurazione il momento di campata originato da g1 vale
Per
il calcolo del momento di campata la configurazione di carico è costituita dal carico
g1 presente su entrambe le campate ed il carico q collocato solo
sulla campata di sinistra.
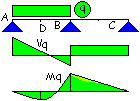
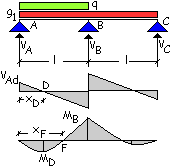
Combinando
l’azione del peso permanente g1 a quella del carico variabile q si
ottiene
|
|
In realtà i due
momenti non si verificano nella stessa sezione. L’approssimazione è a
vantaggio di stabilità. |
Nella
sezione B il momento ridotto risulta pari a
In
corrispondenza di m = 0,2712 (
) si ricava dalla tabella il valore di w0 = 0,3257.
|
|
L’analisi
elastica ha come limitazione |
; oltre tale valore vi sono problemi di incertezza del
modello.L’armatura
necessaria vale, pertanto
Scelta la combinazione
5 f 16 As
= 1005 mm2
con staffe a due
bracci l’interferro risulta
La percentuale di
armatura risulta pari a
Nella
sezione D il momento ridotto risulta pari a
In
corrispondenza di m = 0,1989, (
) si ricava dalla tabella il valore di w0 = 0,2249.
L’armatura
necessaria vale, pertanto
Scelta la combinazione
6 f 12 As
= 678 mm2
con staffe a due
bracci l’interferro risulta
La percentuale di
armatura risulta pari a
Calcolo del
momento di
fessurazione Mcr.
L’area tesa
efficace 
(quota della sezione
di cls che è soggetta alla trazione) è individuata da un’altezza efficace che
assume il minimo dei seguenti valori
Ipotizzato
nella ricerca
dell’asse neutro, si ottiene
che conduce
all’equazione
nella quale è
Posto
si
ottiene
Il momento di
fessurazione Mcr (crack Moment) vale:
nella quale il coefficiente
di durata di applicazione dei carichi è kt=
0,6 (per breve durata) e fct,eff
è il valore medio della resistenza a trazione riferito al tempo in cui si
ritiene possano svilupparsi le lesioni: a lungo termine è 
.
Analisi elastica con
ridistribuzione dei momenti.
Il
momento MB genera il superamento del limite elastico, provocando una
quota aggiuntiva di rotazione della sezione alla quale è associato un momento DM.
DM ha lo stesso verso della rotazione
aggiuntiva ed è quindi di segno opposto rispetto ad MB.
Il
risultato è una riduzione del momento sull’appoggio B
ed
un aumento del momento di campata il cui massimo si sposta verso l’appoggio
centrale.
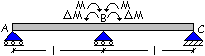
DM dipende dalla capacità rotazionale della
sezione ovvero dalla sua duttilità e quindi dalla profondità della zona
compressa x.
Le Norme Tecniche
consentono il ricorso ad un momento ridotto pari a
nella quale è
con un minimo pari a 
Scelto
si ottiene
al quale
corrisponde la deformazione unitaria
ed un momento
ridotto
Nella ricerca del
valore del momento di campata, per entrambi i carichi, il diagramma dei momenti
dopo la ridistribuzione può essere ottenuto sommando al diagramma elastico
quello originato da DM.
Carico g1. Trave caricata su
entrambe le campate.
Contemporaneamente
alla formazione della cerniera plastica in B si ha un aumento del momento
positivo di campata con un contemporaneo avvicinamento del punto D verso
l’appoggio centrale.
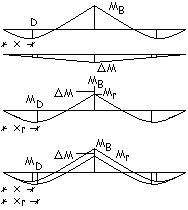
La distanza AD
vale
Il momento in D
vale
Carico q. Trave caricata su una sola campata.
Analogamente a
quanto già visto
la distanza AD
vale
Il momento in D
vale
Il momento di
progetto a ridistribuzione avvenuta vale quindi
Sezione
B
Il
momento ridotto risulta pari a
Essendo
(configurazione di deformazione con xlim = 0,2880,
valore massimo consentito in relazione alla ridistribuzione effettuata) occorre
effettuare il progetto a doppia armatura.
Al
valore di xlim = 0,2880
corrisponde wlim = 0,2331.
|
|
La sezione semplicemente armata è in grado
di sopportare un momento pari a
con un’armatura pari a
ed un’altezza della zona compressa
|
|
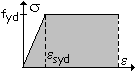
La coppia interna e il diagramma delle
deformazioni |
La
differenza DM tra il momento di progetto MSd
e Mlim è fatta sopportare da una sezione composta dalla coppia di
armature (senza conglomerato) A’s e DAs. Le
armature aggiuntive devono avere il baricentro posizionato alla stessa
altezza della sezione precedente. Il
calcolo dell’armatura aggiuntiva a trazione DAs e
dell’armatura a compressione A’s può essere condotto osservando
che le due forze DS e S’ costituiscono una coppia di forze
di braccio pari a d-d’ il cui momento deve equilibrare il momento esterno DM. |
|
|
Il
coefficiente di utilizzazione dell’acciaio compresso vale
La
tensione è data da |
L’armatura a
compressione risulta pari a
Ai
quali, ipotizzando almeno due barre con funzione di reggistaffe, corrispondono 2
f 12 A’s = 226 mm2
L’interferro
per l’armatura a compressione è pari a
L’armatura
aggiuntiva a trazione vale
L’armatura
necessaria in trazione vale, pertanto
Scelta
la combinazione
5 f
14 As,eff = 769 mm2
con staffe a
due bracci l’interferro risulta
verificato
La percentuale di
armatura a trazione vale
La percentuale di
armatura a compressione vale
Sezione
D
Analogamente
a quanto già esaminato, il momento ridotto risulta pari a
Essendo
(configurazione di deformazione con xlim = 0,2880,
valore massimo consentito in relazione alla ridistribuzione effettuata) occorre
effettuare il progetto a doppia armatura.
Al
valore di xlim = 0,2880
corrisponde wlim = 0,2331.
La sezione semplicemente armata è in grado
di sopportare un momento pari a
con un’armatura pari a
ed un’altezza della zona compressa
Il
coefficiente di utilizzazione dell’acciaio compresso vale
La tensione è data
da
L’armatura a
compressione risulta pari a
Ai
quali, ipotizzando almeno due barre con funzione di reggistaffe, corrispondono 2
f 12 A’s = 226 mm2
L’interferro
per l’armatura a compressione è pari a
L’armatura
aggiuntiva a trazione vale
L’armatura
necessaria in trazione vale, pertanto
Scelta
la combinazione
5 f
14 As,eff = 769 mm2
con staffe a
due bracci l’interferro risulta
verificato
La percentuale di
armatura a trazione vale
La percentuale di
armatura a compressione vale
|
|
Assumendo il
valore minimo di ridistribuzione
si ottiene
al quale
corrisponde
La collocazione
delle armature superiori alla distanza
vale a dire
sotto l’asse neutro (quindi in zona tesa) non avrebbe consentito il progetto
a doppia armatura. Il problema è
originato dal modesto valore dell’altezza che caratterizza le travi in
spessore di solaio. |
|
|
Assumendo valori
di ridistribuzione diversi varia il rapporto tra il momento nelle sezioni B e
D. Con valori di ridistribuzione bassi può verificarsi una crescita troppo
elevata del momento di campata che avrebbe solo l’effetto di invertire la
posizione della sezione più sollecitata passando da B a D. |
|
d |
MB,Sd (kN/m) |
MD,Sd (kM/m) |
|
0,70 |
39,20 |
45,39 |
|
0,75 |
42,00 |
44,67 |
|
0,80 |
44,80 |
43,98 |
|
0,85 |
47,60 |
43,28 |
|
0,90 |
50,40 |
42,58 |
|
0,95 |
53,20 |
41,91 |
|
1,00 |
56,00 |
41,22 |
|
|
Per assicurarsi
il rispetto delle verifiche agli SLE, nella fase del predimensionamento è
opportuno seguire le indicazioni sul
rapporto tra altezza della sezione e luce della trave (Circolare NTC08).
Per
nella quale è K
=1,3 per campate terminali Per la sezione D
si ottiene
Per la struttura
in esame il rapporto di deformabilità vale
|
VerificatoAnalisi plastica.
E’
un metodo di analisi utilizzato per la ricerca del carico massimo sopportabile
dalla struttura più che per il suo progetto.
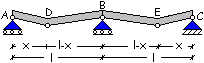
La
sezione sull’appoggio centrale e quelle di campata sono in grado di sopportare
rispettivamente un momento massimo MRd,B e MRd,D = MRd,E.
Poiché le tre sezioni sono armate allo stesso modo si ha MRd,B = MRd,D
= MRd,E.
La
posizione dell’asse neutro può essere determinata risolvendo l’equazione di
secondo grado, valida nel campo 3 con acciaio superiore non snervato
Il
coefficiente di utilizzazione dell’acciaio compresso vale
(acciaio non snervato)
Le
forze interne valgono:
(forza di compressione)
la forza C è applicata ad una distanza dal lembo superiore pari a
La
stessa forza è applicata ad una distanza rispetto al baricentro del
calcestruzzo pari a
110 – 21 = 89 mm = 0,09 m
Per l’acciaio si ottiene
(forza di
compressione) posizionata ad una distanza di
110 – 39 = 71 mm = 0,07 m dal baricentro del calcestruzzo.
posizionata ad una
distanza di 182 – 110 = 72 mm = 0,07 m dal baricentro del calcestruzzo. La
forza è di trazione.
Rispetto al baricentro del calcestruzzo si ha
|
|
Per il segno da attribuire ai momenti,
occorre ricordare che il momento è positivo se produce una trazione in basso
(è il caso della forza S) ed una compressione in alto (la forza C e la forza
S’). |
Al
crescere del carico q sulla struttura il momento elastico MB raggiunge
il valore massimo sopportabile MRd,B
e la sezione assume un comportamento
plastico con la trasformazione dell’incastro interno in una cerniera plastica.
Aumentando
ancora il carico q la rotazione nel punto B aumenta ulteriormente ed i
momenti MD ed ME
crescono anch’essi fino a raggiungere il loro valore massimo MRd,D trasformando
ancora l’incastro interno in cerniera plastica.
La
struttura assume la forma di un meccanismo che anche un piccolissimo ulteriore
aumento del carico q porterebbe in movimento.
Raggiunto il
meccanismo le due campate AB e CD hanno lo stesso comportamento plastico di una
trave con appoggio e incastro per la quale è (sezioni in B, D ed E aventi la
stessa armatura)
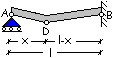
In valore assoluto
è
con 
Per
garantire la formazione della cerniera plastica la sezione deve risultare molto
duttile. Tale obiettivo è raggiunto per
ü acciaio a media o alta duttilità (tipo B e
C)
ü rapporto tra luci contigue compreso tra 0,5
e 2 (nel caso in esame il rapporto è pari ad uno)
(cls fino a C50/60)
Non verificato
Nel
caso di mancata soddisfazione anche di una sola delle condizioni precedenti
l’EC2 richiede una verifica diretta della capacità rotazionale della sezione.
In
pratica:
ü si calcola la curvatura della trave con
l’espressione 
ü si determina la rotazione plastica relativa
al tratto di trave a cavallo dell’appoggio centrale di lunghezza pari a 1,2 h
con l’espressione 
(valore espresso in milliradianti)
ü si verifica che la validità della
disuguaglianza 
attraverso il grafico di riferimento
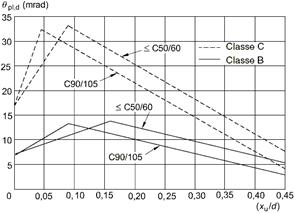
Dal grafico per 
si ricava 
. Verificato.
|
|
Nel
calcolo della distanza x se l’acciaio compresso è snervato è
Nel caso di
semplice armatura è
|
