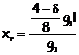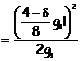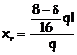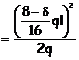Analisi elastica
con ridistribuzioni ed analisi plastica. Cemento armato.
Analisi elastica
con ridistribuzioni ed analisi plastica. Cemento armato.
Per il calcolo delle strutture in c.a. le Norme Tecniche
consentono tre diversi approcci analitici:
Ø
analisi elastica (con o senza
ridistribuzioni dei momenti)
Ø
analisi
plastica
Ø
analisi non lineare
Le caratteristiche dei diversi tipi di analisi sono riassunte
sinteticamente nel quadro seguente nel quale sono presenti le integrazioni
contenute nell’Eurocodice 2 in assenza di indicazioni della norma nazionale.
|
Tipo di analisi |
Caratteristiche |
Note |
|
Elastica |
|
Valida
sia per SLU sia per SLE. Per
|
|
Elastica con ridistribuzione
dei momenti. |
|
Valida
sia per SLU sia per SLE. Per
le ridistribuzioni più consistenti, è opportuno far seguire al calcolo agli
SLU un controllo della deformabilità agli SLE. |
|
Plastica |
Valori
validi per: ü
acciaio
a media o alta duttilità (tipo B e C) ü
rapporto
tra luci contigue compreso tra 0,5 e 2 |
Valida
solo per gli SLU. Se
anche solo una delle condizioni non è rispettata è necessaria una verifica
della capacità rotazionale della sezione.
|
|
Non
lineare |
Esame
delle fasi: ü
elastica
fino al raggiungimento della fessurazione ü
fessurata:
fino allo snervamento dell’acciaio ü
plastica
fino alla rottura |
Valida per
azioni sia statiche sia dinamiche. Origina un
diagramma trilineare (deformazioni non più direttamente proporzionali alle
sollecitazioni) tra momenti e rotazioni.
Richiede l’uso dell’elaboratore |
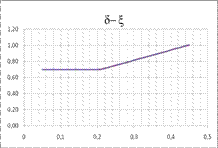
I
riferimenti alle grandezze adimensionali ![]() e
e ![]() sono relativi al campo
di deformazione 3 del diagramma di Rüsch.
sono relativi al campo
di deformazione 3 del diagramma di Rüsch.
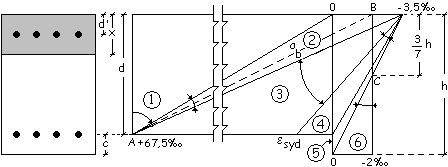
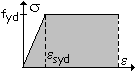
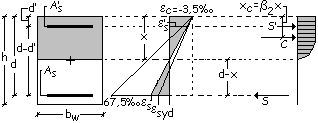
Le
limitazioni ai valori della profondità x dell’asse neutro sono motivate dalla
necessità di disporre di una sezione di media o elevata duttilità; al crescere
dell’estensione della zona compressa, infatti, si ha un aumento di armatura
insieme ad una deformazione unitaria e sempre più vicina al limite plastico ![]() con conseguente riduzione della duttilità.
con conseguente riduzione della duttilità.
|
|
|
Per l’acciaio
B450C si ha
|
Per
meglio chiarire le modalità di calcolo si farà nel seguito riferimento ad una
trave a due campate con luci costanti.
Analisi elastica.
Per
il calcolo del momento sull’appoggio centrale la configurazione di carico è
costituita dal carico g1 ed il carico q presenti su entrambe le
campate.
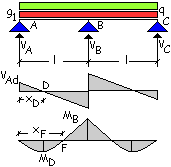
Si ha
![]()
nella
quale, applicando la formula di correlazione agli SLU, è
![]()
|
|
Con
la stessa configurazione il momento di campata vale
tale valore non
è però quello massimo nella sezione considerata. |
Per
il calcolo del momento di campata la configurazione di carico è costituita dal carico
g1 presente su entrambe le campate ed il carico q collocato solo
sulla campata di sinistra.
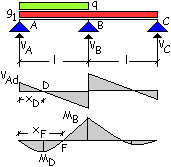
Combinando
l’azione del peso permanente g1 a quella del carico variabile q si
ottiene
![]()
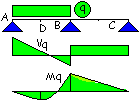
Analisi elastica con
ridistribuzione dei momenti.
Il
momento MB genera il superamento del limite elastico, provocando una
quota aggiuntiva di rotazione della sezione alla quale è associato un momento DM.
DM ha lo stesso verso della rotazione
aggiuntiva ed è quindi di segno opposto rispetto ad MB.
Il
risultato è una riduzione del momento sull’appoggio B
![]()
ed
un aumento del momento di campata il cui massimo si sposta verso l’appoggio
centrale.
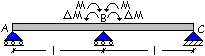
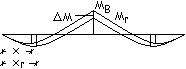
DM dipende dalla capacità rotazionale della
sezione ovvero dalla sua duttilità e quindi dalla profondità della zona
compressa x.
Le Norme Tecniche
consentono il ricorso ad un momento ridotto pari a
![]()
nella quale è
![]() con un minimo pari a
con un minimo pari a ![]()
In altri termini è
possibile ridurre il momento fino al 30%.
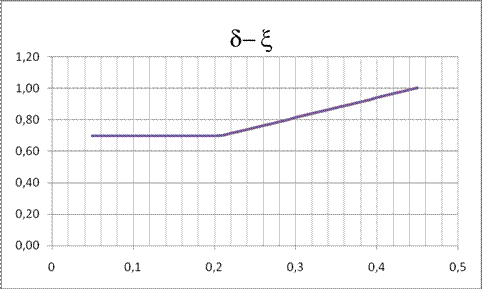
Imponendo
![]()
si ottiene
![]()
al quale
corrisponde
![]()
Come limite inferiore
(nessuna riduzione del momento) si ha
![]()
per
![]()
al quale
corrisponde
![]()
|
|
Oltre il limite Quale
limite inferiore si può assumere il limite con il campo 2 del diagramma di Rüsch per il quale è
|
|
|
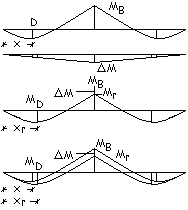
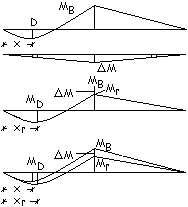
Nella ricerca
del valore del momento di campata, per entrambi i carichi, il diagramma dei
momenti dopo la ridistribuzione può essere ottenuto sommando al diagramma
elastico quello originato da DM. Carico g1. Trave caricata su
entrambe le campate. Contemporaneamente
alla formazione della cerniera plastica in B si ha un aumento del momento
positivo di campata con un contemporaneo avvicinamento del punto D verso
l’appoggio centrale.
La reazione in A
dopo la ridistribuzione può essere calcolata con l’equazione
La distanza AD
vale
Il momento in D
vale
|
|
Carico q. Trave caricata su una sola campata.
Analogamente a
quanto già visto si ha La reazione in A
dopo la ridistribuzione può essere calcolata con l’equazione
La distanza AD
vale
Il momento in D
vale
Il momento di
progetto a ridistribuzione avvenuta vale quindi
|
Procedura
di progetto:
1) si predimensiona la
sezione di calcestruzzo.
2) si fissa il coefficiente di ridistribuzione
e da esso si ricava ![]()
3) si progetta l’armatura a sezione obbligata.
Se nella tabella del cemento armato al coefficiente ![]() corrisponde
corrisponde ![]() si ricorre al calcolo a doppia armatura per rimanere nei limiti
fissati.
si ricorre al calcolo a doppia armatura per rimanere nei limiti
fissati.
|
|
A valori di
ridistribuzione bassi corrispondono valori
modesti ai quali
possono corrispondere valori della posizione dell’asse neutro
minori di quelli
della posizione delle armature superiori
che possono
venirsi a trovare sotto l’asse neutro (quindi in zona tesa). In tale
evenienza non sarebbe possibile il progetto a doppia armatura. Il problema può
verificarsi con il modesto valore dell’altezza che caratterizza le travi in
spessore di solaio. Sempre per
valori di ridistribuzione bassi può verificarsi una crescita troppo elevata
del momento di campata che avrebbe solo l’effetto di invertire la posizione
della sezione più sollecitata passando da B a D. La scelta del valore di
distribuzione dovrebbe tendere a “bilanciare” le sollecitazioni nella trave
facendo avvicinare i valori dei momenti nelle due sezioni. |
|
|
Il calcolo con
ridistribuzione può condurre a sezioni piuttosto deformabili. Per assicurare
il rispetto delle verifiche agli SLE, nella fase del predimensionamento è
opportuno seguire le indicazioni sul
rapporto tra altezza della sezione e luce della trave (Circolare NTC08).
Per
|
|
K |
|
|
Travi
semplicemente appoggiate |
1 |
|
Campate
terminali |
1,3 |
|
Campate
intermedie |
1,5 |
|
Mensole |
0,4 |
|
Valori base dei rapporti l/h |
|||||||||||||||
|
Rck (N/mm²) |
30 |
||||||||||||||
|
fck = 0,83Rck (N/mm²) |
24,9 |
||||||||||||||
|
r = r + r' |
0,15 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
|
Travi
semplicemente appoggiate |
40 |
33 |
26 |
23 |
21 |
19 |
18 |
17 |
17 |
16 |
16 |
16 |
15 |
15 |
15 |
|
Campate
terminali |
52 |
43 |
34 |
29 |
27 |
25 |
24 |
23 |
22 |
21 |
21 |
20 |
20 |
20 |
19 |
|
Campate
intermedie |
60 |
49 |
39 |
34 |
31 |
29 |
27 |
26 |
25 |
25 |
24 |
23 |
23 |
23 |
22 |
|
Mensole |
16 |
13 |
10 |
9 |
8 |
8 |
7 |
7 |
7 |
7 |
6 |
6 |
6 |
6 |
6 |
Analisi plastica.
E’
un metodo di analisi utilizzato per la ricerca del carico massimo sopportabile
dalla struttura più che per il suo progetto.
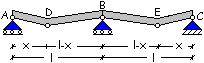
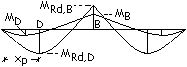
La
sezione sull’appoggio centrale e quelle di campata sono in grado di sopportare
rispettivamente un momento massimo MRd,B e MRd,D = MRd,E.
Se sono munite della stessa armatura si ha MRd,B = MRd,D
= MRd,E.
Al
crescere del carico q sulla struttura il momento elastico MB raggiunge
il valore massimo sopportabile MRd,B
e la sezione assume un comportamento
plastico con la trasformazione dell’incastro interno in una cerniera plastica.
Aumentando
ancora il carico q la rotazione nel punto B aumenta ulteriormente ed i
momenti MD ed ME
crescono anch’essi fino a raggiungere il loro valore massimo MRd,D trasformando
ancora l’incastro interno in cerniera plastica.
La
struttura assume la forma di un meccanismo che anche un piccolissimo ulteriore
aumento del carico q porterebbe in movimento.
Raggiunto il
meccanismo le due campate AB e CD hanno lo stesso comportamento plastico di una
trave con appoggio e incastro per la quale è (sezioni in B, D ed E aventi la
stessa armatura)
![]()
![]()
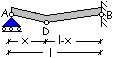
In campata per ![]()
![]() si ha
si ha
![]()
Per
l’equilibrio verticale del tratto AD si ha
![]()
![]()
![]()
![]()
|
|
La
reazione verticale in D è nulla perché nel punto D si ha il massimo momento
ed il taglio è nullo. |
Il
taglio nella sezione alla sinistra di B vale
![]()
![]()
![]()
![]()
Per
garantire la formazione della cerniera plastica la sezione deve risultare molto
duttile. Tale obiettivo è raggiunto per valori
![]() (
(![]() ) (cls fino a C50/60)
) (cls fino a C50/60)
![]() (
(![]() ) (cls fino a C50/60)
) (cls fino a C50/60)
Devono
poi essere verificate le seguenti condizioni:
ü acciaio a media o alta duttilità (tipo B e
C)
ü rapporto tra luci contigue compreso tra 0,5
e 2
Nel caso di
mancata soddisfazione anche di una sola delle condizioni precedenti l’EC2
richiede una verifica diretta della capacità rotazionale della sezione.
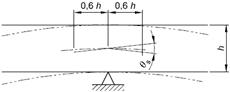
In
pratica:
1)
si
ricava la posizione dell’asse neutro calcolando la distanza x
2)
si
calcola la curvatura della trave con l’espressione ![]()
![]()
3)
si
determina la rotazione plastica relativa al tratto di trave a cavallo dell’appoggio
centrale di lunghezza pari a 1,2 h con l’espressione ![]() (valore espresso in milliradianti)
(valore espresso in milliradianti)
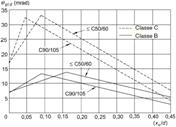
4)
si
verifica che la validità della disuguaglianza ![]() attraverso il grafico di riferimento
attraverso il grafico di riferimento
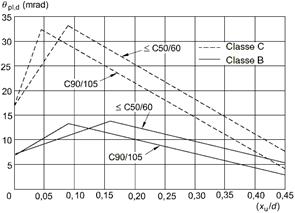
|
|
Calcolo
della distanza x.
Se
l’acciaio compresso è snervato è con Per
verificare lo snervamento dell’acciaio il coefficiente di utilizzazione k’
deve risultare maggiore di 1
con
Se
l’acciaio compresso non risultasse snervato la distanza x si ricava
risolvendo l’equazione seguente
|
Analisi non lineare.
Vengono
analizzate le tre fasi principali che caratterizzano il comportamento della
struttura:
ü fase elastica fino al raggiungimento della
fessurazione
ü fase fessurata: fino allo snervamento
dell’acciaio
ü fase plastica: fino alla rottura
L’analisi non
lineare è un metodo più approfondito di indagine rispetto a quelli esaminati in
precedenza ed i suoi risultati sono validi in presenza di azioni sia statiche
sia dinamiche.
Origina un
diagramma trilineare (deformazioni non più direttamente proporzionali alle
sollecitazioni) tra momenti e rotazioni.
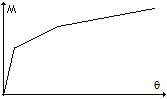
Al
termine della fase elastica il calcestruzzo, inizialmente interamente reagente,
raggiunge in corrispondenza del bordo teso la sua resistenza a trazione dando
inizio così al fenomeno della fessurazione.
Per
il calcolo del momento di fessurazione si considera una sezione inferiore tesa
costituita dalle armature e da un’area di calcestruzzo in trazione di altezza
efficace pari ad hc,eff ed un’area superiore compressa di
calcestruzzo.
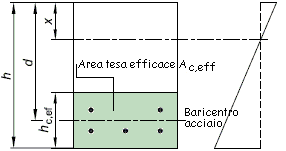
Come
altezza dell’area efficace si assume il minimo dei valori seguenti
![]()
L’area
dell’acciaio viene “omogeneizzata”, trasformandola in un area equivalente di
calcestruzzo, moltiplicandola per il coefficiente
![]()
con
![]()
La tensione di
calcolo a trazione del conglomerato fct,eff è il valore medio della
resistenza a trazione riferito al tempo in cui si ritiene possano svilupparsi
le lesioni: a lungo termine è ![]() (resistenza media a trazione).
(resistenza media a trazione).
|
Rck (N/mm²) |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
|
|
27267 |
28821 |
30200 |
31447 |
32588 |
33643 |
34625 |
35547 |
36416 |
|
|
1,61 |
1,95 |
2,27 |
2,56 |
2,83 |
3,10 |
3,35 |
3,60 |
3,83 |
Il momento di
fessurazione Mcr (crack moment) è dato dalla
![]()
nella quale il coefficiente kt
di durata di applicazione dei carichi vale kt= 0,6 per carico di breve durata,
kt=0,4 per azioni di lunga durata (Circolare NTC08).
Nella seconda
fase che conduce allo snervamento dell’acciaio (fase fessurata) può tenersi
conto del contributo positivo che il calcestruzzo compreso tra una fessura e
l’altra esercita nei confronti dell’acciaio limitandone le deformazioni (fenomeno
del tension stiffening).
La terza ed ultima
fase consiste nella plasticizzazione dei due materiali con conseguente aumento
delle rotazioni causato dalla formazione di una cerniera plastica nella
sezione.
Da quanto esposto
emerge che questo tipo di analisi è abbastanza complesso dal punto di vista
numerico e va quindi affrontato con l’uso dell’elaboratore.
I risultati che ne
derivano non si discostano sostanzialmente da quelli raggiunti con un’analisi
lineare caratterizzata dal massimo della ridistribuzione dei momenti o con
l’analisi plastica.