The Planck black hole and the quantization of its mass yields new mathematical relationships among basic constants even if a dimensional mismatch may appear at a cursory glance. Actually all equations are balanced once the quantization of the Planck mass and quantity wu are taken in account. All numbers are in accordance with the MKSA system even if its definition of electrical quantities are not easily integrated with quantum gravitation. The Codata value for the Planck time is numerically very close to the ratio between gravity and electric force in an electron: its difference, disregarding a π√2 factor, is only 0.2%. This is not a coincidence as they both refer to the same particle and the small difference is between a rotating and a non-rotating particle.
This numeric table is a summary of what can be found in more details in the papers that follows. The initial G is close to the experiment using atom interferometry (Rosi et al. 2014) but it will be in line with the Codata recommended value if we consider a small variation from its initial value.
|
Basic data | Nov. 2024 |
||
| c = 299792458 h = 6.62607015x10-34 G = 6.6729196595x10-11 | ||
|
Stationary particle - Planck black hole |
||
|
Planck time tp |
(πhG/c5)1/2 |
2.395019985x10-43 |
|
Planck mass M |
h/tpc2 |
3.078261296x10-8 |
|
Quantized Planck mass M0 |
M tp1/2 |
1.50646849x10-29 |
|
Planck permittivity εp |
(tp /4π2)1/4 |
8.82546x10-12 |
|
Planck charge Q |
M(4πεpG)1/2 = (4εphc)1/2 |
2.648116196x10-18 |
|
Rotating particle - initial electron state |
||
|
Toroidal ratio unitary charge2/unitary time wu |
(2π)4Q u2/tu |
1558.54545654 |
|
Initial fine structure α0 |
(wu tp /Q2)1/2 |
7.295873076x10-3 |
| Initial Newton's G with current data | (c5/πh)(α(2-α)e2/wu )2 | 6.6729196384x10-11 |
|
Relations among constants - electron charge e = 1.602176634x10-19. Adopted charge e1 = 1.6021766353x10-19 |
||
|
Fine structure constant α |
1-(1-wu tp /e12)1/2 |
7.297352564x10-3 |
|
Measurable Newton's G |
(α(2-α)/α0(2-α0))(c5/πh)(α(2-α)e12/wu )2 |
6.6742678666x10-11 |
| Permittivity ε0 | εp α02/α2(1-α /2)(e1/e)2 | 8.8541878192x10-12 |
|
Electron data |
||
| Charge e1 | (wu tp /α(2-α))1/2 | 1.6021766353x10-19 |
| Mass me | M0(α /2)1/2(α /α0)12((1-α /2)(2-α)/(2-α0))3/8 | 9.109383715x10-31 |
|
Bohr magneton μB |
(Qħ/M0)(α0/α)13(1-α/2)1/8((2-α0)/(2-α))3/8/(2-α)(e1/e) |
9.2740100648x10-24 |
| Compton wavelength λc |
πGM2/mec2 |
2.42631023514x10-12 |
|
Electric force Fe=e2/4πε0 |
Q2/4πεp(2/α) |
2.3070775544x10-28 |
|
Gravitational force Fg=Gme2 |
tp
ħ
c
α
(α
/α0)24((1-α
/2)(2-α)/(2-α0))3/4 = πε03e2((e1/e)2(α/α0)8(1-α/2))4((1-α/2)(2-α)/(2-α0))3/4 |
5.537246899x10-71 |
|
Gravitational /electric force ratio Fg /Fe |
tp (α /α0)24((1-α /2)(2-α)/(2-α0))3/4 = (2/α)(me /M)2 |
2.40011303x10-43 |
Presentation:
Connecting Fundamental Constants - pdf, 4 pages, 2008
Connecting Fundamental Constants - pdf, 14 slides, Nov. 2024
Detailed documents:
Magnetic Anomaly in Black Hole Electrons - pdf, 10 pages, Sept. 2024
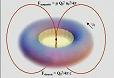A model for a black
hole electron can be developed starting from three basic
constants: h, c and G.
The quantization of the Planck mass gives a description of
the electron with its own associated mass and charge. The
precise determination of its rotational speed yields
accurate numbers, within one standard deviation, of all
quantities, including, once a small change in the fine
structure constant is considered, its magnetic moment and
its magnetic moment anomaly.
Planck
Permittivity and Electron Force - pdf, 7 pages, Sept. 2024
The Planck permittivity is derived from the Planck
time and becomes an important parameter for the definition of a
black hole model applied to Planck quantities. The emerging
particle has all the features of a black hole electron and a
precise evaluation of its gravitational and electric force is
now possible.
Reality of the Planck Mass - pdf, 10 pages, Sept. 2024
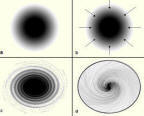
The Planck mass is not the elusive particle so often depicted and if it is considered as a black hole then its quantization via the Planck time will originate the electron mass and charge. The faster the rotation of the Planck mass the lower its measurable mass. At the speed of light we are left with a massless and chargeless particle identified with the neutrino and the interaction of the Planck charge with virtual particles in the vacuum would yield the charge for the d-quark. One of the solutions of the vacuum equation is a negative fine structure constant implying a speed slightly faster than light and an imaginary electron.
Electric
Force from Gravitational Variation - pdf,
12 pages, Sept. 2024
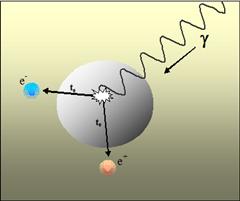The
quantization of the Planck mass seems to place a limit on
the measurable energy or mass. In addition, rotation of
this mass together with its electric and magnetic
properties give us the link between gravity and
electricity. The result is not just a unified field but
rather a field we always experience in its duality:
electric and gravitational. Now we could calculate the
electric field generated by the variation of the
gravitational field due to the electron materialization
without the knowledge of its charge. As an approaching
mass is equivalent to a variation of its gravitational
field, the resulting electric field may influence the
measured gravitational force. This means that even the
measurement of the constant of gravitation could be
influenced by moving masses.
