A.G.a.Fe (Algebraic Geometry at
Ferrara)
L’opera di
Weierstrass sulle funzioni ellittiche
Karl Theodor Wilhelm Weiestrass dopo essere rimasto per volere del padre quattro
anni presso la Facoltà di legge dell’Università di Bonn, nel 1839 si iscrisse all’Università
di Münster per ottenere il diploma di
insegnante di matematica nelle scuole superiori. Qui seguì le lezioni di Christoph Gudermann sulle funzioni
ellittiche e poté mettere a frutto gli studi di matematica ai quali si era
autonomamente dedicato durante la sua permanenza a Bonn. Weierstrass aveva
raggiunto una forte preparazione che gli permise di leggere anche i lavori di
Abel sulle funzioni ellittiche e il Fundamenta Nova di Jacobi. Gudermann conosceva molto bene l’opera di Jacobi
e fu in Germania uno dei primi a svolgere corsi sulle funzioni ellittiche. Il
suo insegnamento influenzò moltissimo il giovane Weierstrass ed infatti egli
nutrì sempre grande ammirazione e rispetto per il suo maestro come si evince dalle sue stesse parole: “da
quando sono stato introdotto alla conoscenza della teoria delle funzioni
ellittiche dal mio maestro Gudermann, questo ramo relativamente nuovo
dell’analisi matematica ha esercitato su di me una forte attrazione ed è stato
ed è fattore determinante nei miei interessi matematici” (Werke Mathematische, I,
pp. 223–224).
Se
Legendre aveva ridotto gli integrali ellittici a tre forme standard contenenti
la radice quadrata di un polinomio di quarto grado, Weierstrass pervenne a tre
forme diverse contenenti la radice quadrata di un polinomio di terzo grado
(Werke II, pp. 245–255), e cioé
e
introdusse come funzione ellittica fondamentale quella che risulta
dall’inversione del primo integrale. Cioè se 
allora la funzione x di u
è la funzione di Weierstrass:
. Ricordiamo che
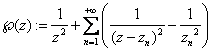(1)
ove
zn è un punto di Г. In particolare la 
è meromorfa su C ed ha poli esattamente nei punti
di Г. Affinché non degeneri in una funzione
esponenziale o trigonometrica è necessario che il discriminante 
sia diverso da 0, cioè che le tre radici del polinomio
di terzo grado in x siano tutte
distinte. La funzione doppiamente periodica di Weierstrass svolge il ruolo di snu nella teoria di Jacobi e fornisce
l’esempio più semplice di funzione doppiamente periodica. Weierstrass dimostrò
che ogni funzione ellittica può essere espressa molto semplicemente in termini di e della sua derivata.
In particolare la funzione ha residuo zero nei
poli, allora per ogni cammino γ chiuso in C tale che 
si ha che 
Ciò significa che 
è integrabile nella regione C\ Г, dunque essa è la derivata di una funzione meromorfa su C.
Denotiamo ζ(z) la funzione cha ha per derivata 
e che soddisfa la condizione 
. Essa è detta funzione “zeta di Weierstrass”. Da (1) siamo
condotti all’espressione esplicita
.
Si
ponga poi
,
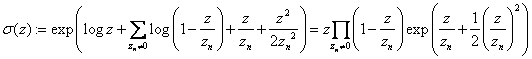questa
è una funzione ad un sol valore che soddisfa la condizione 
. La σ(z) è
una funzione intera dispari (in particolare σ(0)=0). Inoltre la funzione σ(z) detta funzione “sigma di Weierstrass” soddisfa l’equazione
differenziale 
. Possiamo perciò
enunciare il seguente teorema:
Teorema Sia f(z) appartenente a E(Г) e siano a1 ,…, ak ,
zeri di f e b1 ,…, bk poli di f tali che a1 +…+ak – b1 –…– bk =0. Allora
esiste una costante A tale che 
. In particolare ogni
funzione ellittica è determinata, a meno di una costante moltiplicativa, dai
suoi zeri e dai suoi poli.
Le
ricerche ed i risultati di Weierstrass conferirono grande eleganza alla teoria
delle funzioni ellittiche. Per Weierstrass il problema centrale della teoria
delle funzioni ellittiche fu quello di determinare tutte le funzioni complesse Ф per le quali esiste un teorema
di addizione algebrico, ossia per le quali Ф(z+w) dipende algebricamente da Ф(z) e da Ф(w) (cfr. Formeln und lehrsatze zum gebrauche der
elliptischen functionen, p. 1).
Egli trovò che ogni funzione per la quale esiste un teorema di addizione
algebrico è una funzione ellittica o (come casi limite) una funzione razionale,
trigonometrica o esponenziale.
