conforto

A.G.a.Fe (Algebraic Geometry at Ferrara)

Fabio Conforto e il suo trattato

“Abelsche Funktionen und Algebraische Geometrie”

Il trattato Abelsche Funktionen und Algebraische Geometrie è una rielaborazione delle note delle lezioni tenute da Fabio Conforto nell’anno accademico 1940-41 presso l’Istituto Nazionale di Alta Matematica, pubblicate col titolo Funzioni abeliane e matrici di Riemann presso la Libreria dell’Università di Roma nel 1942. Lo stesso Conforto in una lettera ad Erhard Schmidt datata 29 Dicembre 1951 scrive:

“Io mi propongo di riscrivere tutto il testo ancora una volta ex-novo, usufruendo della mia redazione del 1942, la quale rimane in un certo senso come il nucleo intorno al quale si sviluppa la nuova trattazione”.

In Funzioni abeliane e matrici di Riemann, Conforto riprende le teorie classiche sull’argomento, originate dalle ricerche di Jacobi, Riemann, Weierstrass, Poincaré, Krazer, e le presenta sotto una nuova forma assai più coerente e naturale, svolgendo in tutti i dettagli un’idea che era stata realizzata nel 1891 da Paul Emile Appell, limitatamente però al caso delle funzioni di due variabili, e ventilata poi in generale nel 1928 dal Solomon Lefschetz (vedi oltre). La stessa idea, indipendentemente dal Conforto, fu seguita nel 1948–49 da Carl Ludwig Siegel e André Weil, infatti l’opera di Conforto non ebbe la diffusione che si sarebbe meritata, poiché pubblicata durante il periodo bellico in veste litografica e tiratura limitata. Nell’introduzione Conforto scrive:

L’origine storica della teoria delle funzioni abeliane è da ricercarsi nel problema di inversione sopra una curva algebrica C di genere p, posta da Jacobi nel 1829. Siano infatti:

p integrali abeliani di prima specie, linearmente indipendenti, sopra C e si ponga:

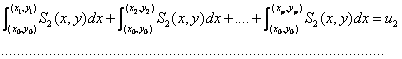
dove è il punto di C. Immaginando fissato l’estremo inferiore (x₀,y₀), il teorema di Abel implica che comunque fissati comunque u₁, u₂, ….., u_p rimane individuato il gruppo di punti (x₁ ,y₁ ), (x₂ ,y₂ ),…,(x_p ,y_p ) (o eccezionalmente, una serie lineare g_p su C). Se però u₁, u₂, ….., u_p si incrementano di ω₁, ω₂, ….., ω_p dove ω_i (i=1,2,…,p) indica il periodo dell’integrale percorso lungo un ciclo qualsiasi tracciato sulla superficie di Riemann relativa a C, si ottiene sempre lo stesso gruppo di p punti. Da qui scende che il gruppo dei punti (x₁ ,y₁), (x₂ ,y₂),…,(x_p ,y_p) , o più precisamente una funzione simmetrica delle coordinate dei punti del gruppo è una funzione uniforme e meromorfa di u₁, u₂, ….., u_p , la quale possiede il sistema simultaneo di periodi ω₁, ω₂, ….., ω_p tale cioè che il valore della funzione rimane inalterato quando u_i si incrementa di ω_i (i=1,2,…p) . Poiché sulla riemanniana di C esistono 2p cicli indipendenti, la funzione di cui trattasi, possiede 2p sistemi di periodi simultanei.

Le funzioni che si ottengono dal problema di inversione sono appunto le funzioni abeliane. La risoluzione effettiva del problema di inversione, sostanzialmente contenuta nei lavori di Abel e Jacobi per p=1, fu ottenuta successivamente da Gopel e Rosenhain per p=2 ed infine da Riemann e Weierstrass per p qualunque, a mezzo delle cosiddette serie θ, considerate da prima da Jacobi per p=1. Dopo Riemann e Weierstrass, la teoria delle funzioni abeliane si è sviluppata, anche al di là del problema di inversione, essendosi constatato che esistono funzioni uniformemente meromorfe, dotate di 2p sistemi di periodi simultanei, le quali sono più generali delle funzioni che risultano dal problema di inversione, che porta soltanto, secondo la denominazione di Poincaré, alle funzioni abeliane speciali.

Conforto osserva poi che volendo dare un’esposizione sistematica della teoria delle funzioni abeliane, non possono non apparire naturali i due seguenti criteri:

a) iniziare lo studio dalla definizione di funzione abeliana come funzione analitica meromorfa di p variabili, dotate di 2p sistemi di periodi simultanei; attaccarsi così alle funzioni abeliane più generali trascurando in un primo momento le funzioni abeliane speciali: il problema di inversione ed i rapporti tra funzioni abeliane e curve algebriche vengono ridotti così al rango di applicazioni, per quanto di somma importanza, della teoria generale: e troveranno posto più avanti, nello studio di classi speciali di funzioni abeliane.

b) Dedurre direttamente dalla definizione di funzione abeliana la possibilità di esprimere tali funzioni mediante il quoziente di due funzioni intermediarie ed arrivare quindi a dimostrare che le funzioni intermediarie si esprimono per mezzo di serie, le quali hanno necessariamente la forma delle funzioni θ. Nella realizzazione di questo programma, le condizioni necessarie e sufficienti, alle quali deve essere soddisfare la matrice dei periodi perché esistano le corrispondenti funzioni abeliane, si presenteranno naturalmente, come conseguenza dell’esistenza delle funzioni intermediarie. La via tratteggiata conduce dunque al possesso:

A) del teorema di esistenza delle funzioni abeliane;

B) della teoria delle funzioni intermediarie, che viene adoperata nelle applicazioni, specialmente geometriche;

C) della teoria delle funzioni θ mediante le quali si ha una comoda espressione analitica delle funzioni abeliane.

E tutto ciò senza che, in alcun punto, vengano introdotti nozioni e concetti, dei quali non appaia necessariamente e naturale l’introduzione. Ricordiamo che questo programma era stato sviluppato nella memoria di Appel e Frobenius (v. pag. precedente).

Nelle lezioni di Conforto, il contenuto della memoria di Appell viene generalizzato ad un qualunque valore di p, di modo che, usufruendo ad un certo punto dei risultati di Frobenius, si ha la realizzazione completa del programma sopraindicato.

home