Eudosso

L'astronomo Eudosso nacque a Cnido, in Asia Minore, intorno al 408 a.C., e morì verso il 355. Poco più che ventenne, si recò ad Atene, dove seguì le lezioni di Platone, negli anni in cui vi entrava a far parte anche Aristotele. Insoddisfatto, si dice, di ciò che aveva imparato in Grecia, intorno al 378 andò in Egitto, munito di lettere di raccomandazione firmate dal re di Sparta Agesilao, e vi rimase almeno un anno, istruito da un sacerdote di Eliopoli. Nelle Questioni naturali, Seneca afferma che Eudosso acquistò qui la conoscenza dei moti planetari, anche se molti ne dubitano, poiché sembra che a quell'epoca in Egitto la geometria non avesse raggiunto livelli eccelsi. Nella storia dell'astronomia, Eudosso si distingue anche per aver proposto per primo il ciclo solare di quattro anni - i primi tre di 365 giorni e il quarto di 366 - che sarebbe stato introdotto trecento anni dopo da Cesare.
Il risultato più rilevante dei suoi studi fu l'elaborazione del cosiddetto modello delle sfere omocentriche, un ingegnosissimo sistema cosmico che intendeva spiegare le singole particolarità del moto dei pianeti: varie sfere aventi lo stesso centro, ma assi diversi, vengono trascinate nella rotazione le une dalle altre, componendo così tutti i moti voluti. Egli suppose che le sfere fossero situate una dentro l'altra, e che tutte fossero concentriche alla terra (da qui il nome di sistema omocentrico). Benché questa limitazione non spiegasse i fenomeni più complicati, il sistema ne guadagnava in simmetria e in bellezza, e risultava più ragionevole di tanti altri sistemi di cerchi eccentrici, cioè dotati di centri diversi. In pratica, ogni corpo celeste era situato sull'equatore di una sfera che ruotava con velocità uniforme intorno ai suoi due poli. Per spiegare sia le fermate e le retrogradazioni dei pianeti, sia il loro moto in latitudine, Eudosso suppose che i poli di una sfera planetaria non stessero immobili, ma fossero trasportati da una sfera più grande, concentrica alla prima, che ruotava con velocità diversa intorno ad altri due poli. Siccome ciò non bastava ancora a rappresentare i fenomeni, Eudosso collocò i poli della seconda sfera sulla superficie di una terza sfera, concentrica alle precedenti e più grande di esse, la quale ruotava a sua volta su altri due poli con una velocità propria.
Così ragionando, risultò che, con un'appropriata scelta di poli e velocità di rotazione, si poteva rappresentare il moto del sole e della luna supponendo tre sfere per ognuno di questi corpi, mentre per i moti più intricati dei cinque pianeti erano necessarie quattro sfere. Inoltre, le sfere che muovevano ciascun pianeta dovevano essere indipendenti da quelle degli altri. Considerato che per le stelle fisse era sufficiente una sola sfera che producesse la rotazione diurna del cielo, il numero complessivo di sfere era ventisette.
Eudosso espose il suo sistema in un libro "sulle velocità" che è andato perduto, come gli altri suoi scritti. Aristotele, che apparteneva alla generazione successiva, conobbe il sistema di Eudosso grazie a Polemarco, che aveva incontrato personalmente l'autore. Il sistema venne poi descritto dettagliatamente nella storia dell'astronomia di Eudemo, andata perduta, e successivamente in un'opera sulle sfere scritta da Sosigene, un filosofo peripatetico vissuto nella seconda metà del II secolo d.C.: anche quest'opera andò perduta, ma un lungo estratto di essa ci è stato tramandato nel commentario di Simplicio al De caelo di Aristotele, ed è così che possediamo un'esposizione particolareggiata del sistema di Eudosso.
Pare che Eudosso non abbia approfondito la causa di tutte le rotazioni, e nemmeno lo spessore o le reciproche distanze delle sfere. Il suo modello era matematico, inteso solo alla descrizione del moto, mentre il modello costruito in seguito da Aristotele, che prevedeva cinquantacinque sfere, era meccanico, in quanto si preoccupava di come il moto era trasmesso da una sfera all'altra.
Il modello omocentrico, com'era prevedibile, non sopravvisse a lungo, poiché non riusciva a spiegare tutte le osservazioni: se un pianeta era sempre alla stessa distanza dalla Terra, non si capivano le sue variazioni di luminosità, ben note agli astronomi antichi. I sistemi di Ipparco e Tolomeo finirono per soppiantare quello di Eudosso, e gli storici dell'astronomia, senza riuscire ad apprezzarne la finezza, si limitarono a poche osservazioni sulla sua assurdità. Il fatto che, da un punto di vista matematico, il sistema fosse di grande eleganza, sembra non avere interessato nessuno, finché l'astronomo tedesco Christian Ludwig Ideler vi richiamò l'attenzione e ne spiegò i princìpi in due documenti del 1828 e 1830, editi negli atti dell'Accademia di Berlino.EUDOSSO DI CNIDO (408-355 a.C.)
Eudosso fu uno dei più creativi matematici e astronomi Greci. Egli propose un ingegnosissimo sistema astronomico : spiegò il moto del sole, della luna, dei pianeti attraverso una serie di sfere concentriche. Per giustificare i principali movimenti della luna, ad esempio, egli suppose l'esistenza di tre sfere concentriche, ciascuna delle quali ruotava con una ben precisa velocità angolare e attorno ad assi diversamente inclinati. la teoria planetaria era più complessa; egli ad esempio usò 4 sfere per ogni pianeta (la quarta sfera serviva per giustificare il moto retrogrado): in totale il sistema di Eudosso prevedeva 27 sfere così ripartite:

Stelle n° di sfere 1
Sole " 3
Luna " 3
Cinque pianeti " 20

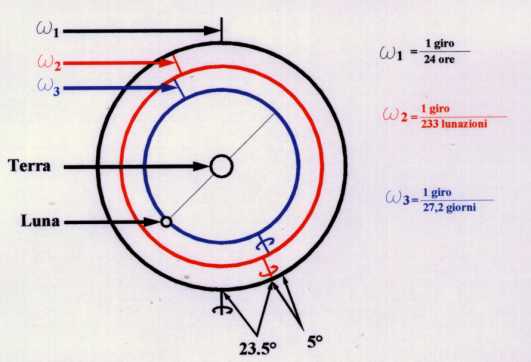
Sembra che Eudosso vedesse la sua teoria come un sistema matematico piuttosto che fisico. Le sue sfere erano tecniche di calcolo più che entità che possedevano reale consistenza. Infatti , essendo tutte le sfere concentriche alla terra i corpi celesti da essi trascinati dovrebbero rimanere ad una distanza costante dalla terra e dunque non variare in luminosità: in realtà la variazione di luminosità dei pianeti non può essere trascurata da nessun osservatore . Inoltre se le sfere fossero reali, il moto delle sfere più esterne dovrebbe trascinare quelle più interne, rendendo così necessaria la presenza di "qualcosa" che dovrebbe distruggere il moto delle sfere esterne.