Cartesius.01
is a freeware program in Demo version, written in Visual Basic 6. It produces
sundials. It includes software that is no longer available in DOS version on http://digilander.iol.it/sundials.
Cartesius.01 is easy to use – it
has one basic screen with easy-to-follow commands. Click TYPES OF SUNDIALS in the top left-hand corner and the following list
appears:
FLAT
1)
Vertical light graph;
2)
Declining - reclining or inclining: 3D method (North and South dials);
3)
Declining - reclining or inclining former projective method;
4)
Declining - reclining or inclining latter projective method;
5)
Vertical (North and South dials): 2D method;
6)
Vertical (special and optimised, default): spherical trigonometry method , this
is the program that comes up automatically at the start-up.
CYLINDRICAL
7)
Circular cross-section: 3D method;
8)
Circular cross-section: parametric method;
9)
Circular cross-section by spherical trigonometry;
10)
Circular cross-section: projective method;
11)
Parabolic cross-section: 3D method.
Cartesius.01
allows the user to produce an image of a flat or cylindrical sundial, on screen
or on paper. Cylindrical sundials are generated on a flat surface and can then
be simply adapted to the cylinder. Program 6, which applies only to the Northern
Hemisphere, permits a more realistic image of the sundial to be produced,
because parts superfluous to the sundial have been eliminated. The different
parts of the quadrant can be shown individually or all together by using
different commands. Another program, Vertical light graph, shows the hidden
features. The graph can be superimposed on the one obtained from program 6. This
way, the hidden features are also visible in the background. The graphs that
appear on the screen can even be printed on a scale of 1:1 by selecting and
highlighting different rectangular areas equivalent to an A4 or A3 sheet of
paper. Almost all of the programs included in Cartesius.01 are capable of drawing astronomical hours, local hours
or hours belonging to a specific longitude. These can be activated by clicking
on "Standard Meridian Time". It is also possible to plot time
according to the old Italic or Babylonian systems. The mean time analemma can
also be inserted at any point, by varying the longitude. Program 6 also offers
the possibility of using a conical style, preferably with Italic or Babylonian
hours. The use of a conical style allows for Italic and Babylonian hours to be
read on a normal quadrant that bears astronomical hours. To make it easier to
learn to use Cartesius.01, the
program carries default values so that if you simply click on Run
the program automatically produces a sundial.
Program
no. 2, (click on "types of sundials" and select from the menu), can
produce any type of flat sundial. It has been produced using three-dimensional
analytical geometry. It is therefore possible to select either independent
variable x or y, leaving z as a dependant variable. For south-facing sundials,
variable x must be used, whereas for those facing east or west, y must be chosen.
Program 2 can generate almost any type of sundial in both the northern and
southern hemispheres.
Program
no. 5 has been produced using two-dimensional analytical geometry and so permits
the creation of a vertical quadrant practically anywhere. As to programs 3 and
4, these two are unusual programs that use the projection method, which only
works for flat sundials, but they have some limitations. These programs have
been placed here purely out of scientific zeal, as have nos. 8, 9, 10 and 11, in
the hope that they may be of interest. The projection method creates areas of
shadow which cannot be completely eliminated and which are due to the very
nature of the method. In both cases a quadrant known as a source is used, which
in program 3 faces south precisely, whereas in 4 it is a flat vertical quadrant
with variable declination. In the former case the element quadrant is fixed
while the receiving quadrant is variable. In the latter case the opposite
happens. The two programs allow the user to compare an inclined vertical
quadrant with a vertical one. Carry out the following test with program 4: use
the following values: j = 40, d =
20, l = 0 and iz = 20. Then click on Data
where the following alternative values should appear: j’ = 58.23611, d’ =
29.84838 and l = -12.8391. Choose Program 1 and insert these new values without
deleting the graph you have. Click on Standard
Meridian Time and then Run. The
new image should superimpose itself precisely over that of the inclined quadrant.
With
Cartesius.01 you can plot sundials on screen, and print them out,
using different mathematical solutions. For cylindrical sundials with a circular
cross-section, four different methods are put forward.
Program
7 uses 3D analytical geometry. It uses a perpendicular style which is always
aligned with the centre of the cylinder. However, the
program constructs the triangle of the style using the style itself and
an inappropriate gnomon fs that runs
from the tip of the style, or perpendicular style, to the cylinder, the
intersection with the cylinder being perpendicular to the element, which passes
through the centre of the dial from which the style emerges. Choosing a
perpendicular style has permitted the creation of a program that is capable of
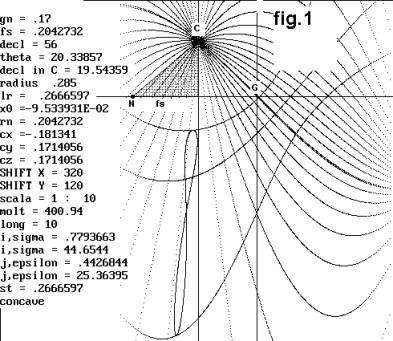
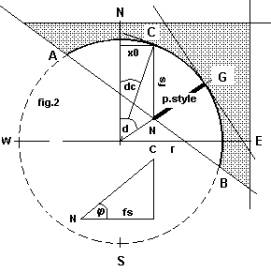
producing any cylindrical sundial, be it concave or convex, with a circular
cross-section. The declination of the dial, in this program, means that of the
plane which is tangential to the cylinder along the "element" that
passes through the foot G from which the perpendicular style emerges. This, and
the use of programs 7, 8, 9, 10 and 11, is illustrated in figures 1 and 2.
Program
8, which concerns a cylindrical sundial of circular cross-section, uses
parametric equations. It takes the cylindrical sundial as the locus of points
common to the cylinder and to the flat dials lying on the declining tangential
planes. All these flat dials have the same tip of the style and the same line of
the horizon as the cylindrical sundial. In this case, the plane that is
tangential to the cylinder along the "element", which passes through
the centre from which the style emerges, is taken as the declination of the
cylindrical sundial. Program 9 uses spherical trigonometry. Program 10 is based
on the projective method. In this last case, a vertical dial for which the
declination is known is projected onto the cylinder from the tip of the style,
thus generating a cylindrical sundial. It is possible to check the accuracy of
these four methods by generating a cylindrical sundial on screen using one of
these methods and then, without deleting the image obtained, repeating the
entire operation using each of the other three methods. Each successive image
should superimpose itself exactly over the previous sundial.
The last case, number 11, is purely
theoretical. It concerns a cylindrical sundial with a parabolic cross-section.
In this case, as in the previous one, the perpendicular style is used. In order
to pinpoint the dimensions of the cross-section parabola, those of the
osculating circle at the vertex are used - they supply the proportions of the
parabola quite adequately. Declinations of no more than 20° are recommended so
that the image does not go off the screen. Click on Section to see a cross-section of the chosen cylindrical sundial
along with the position of the perpendicular style and the figures pertaining to
the triangle of the style, where one exists.
The
speed of execution depends on the program selected, the number of functions
employed and the computer used. Programs that use spherical trigonometry are the
slowest because of the complexity of the calculations carried out, followed by
those that use the parametric method, then the projective method and then 3D
analytical geometry. The fastest is probably no. 5 because it mainly uses LINE
functions. Cartesius.01, the
anthology that brings these programs together, has scroll and zoom functions. It
is also possible to move the axes and widen the screen.
With
Cartesius.01, the values for latitude and longitude can be entered
in both sexagesimal and decimal form. Click on Tools and open the Utilities
Board to convert figures from one format to the other. You can also
calculate the declination of a sundial in the same window. There are illustrated
instructions to make to easier to understand and use the method whereby sun’s
southern azimuth is used for the northern hemisphere and vice versa. It is even
possible to obtain the current figures for the time equation and other
interesting data such as when the sun crosses the meridian and sunrise and
sunset times that take into account the effect of light refraction. The
bibliography contains a list of the books I consulted in devising these
calculations. The sun’s azimuth for the northern hemisphere is positive when
measured anticlockwise from north. Likewise the declination and the inclination
of zenith-type sundials take the opposite sign in the southern hemisphere to
those in the northern hemisphere.
The
algorithm that generates the values in the time equations was taken from
"Astronomia Sferica e Teorica" a book by Francesco Zagar, published by
Zanichelli, 1988. I would like to express particular thanks to my son, Andrea
William, analytical programmer, without whose help this project would never have
been possible.
It
would be very much appreciated if users would signal any problems with the
programs to the authors as it will help us to produce improved versions.
Versions prior to n°91 contained flaws, and problems ensued when attempting to
draw limit sundials. Since then, subsequent versions have been significantly
improved to reduce the risk of such problems arising to a minimum.
Cartesius
is the demo version of a freeware program. It is made available to users in its
current form and with no guarantees as to its functioning. Use of the product is
freely permitted but any sale thereof is strictly forbidden by law. The authors
own the intellectual property rights to the program. They take no responsibility
for any malfunctions or any consequences arising from improper use of the same.
Riccardo Anselmi, December 2003.
See also..
Astrolabium Home page