LA TESI del TEMPO
Multidimensional
Math
Non-Flash Version
Versione Multidimensionale del Non - Flash per la matematica
La teoria di Superstring descrive un mondo formato almeno da 10 dimensioni. Per la maggior parte di noi (con il nostro senso di pensare ed il senso in cui sperimentiamo il mondo) è difficile da immaginare più di tre dimensioni spaziali. Nella matematica, tuttavia, non funzionante in più di tre dimensioni, il problema si risolve, al contrario, con altri strumenti.
Ecco un esempio :
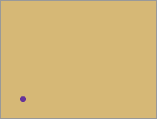
Il
punto non ha dimensioni
"A" non ha larghezza, altezza e profondità. Non ha dimensioni e non ha numeri necessari per essere descritto. Potremmo descrivere una posizione dove un punto esiste con i numeri se desiderassimo dare la relativa posizione, ma ora ci preoccupiamo soltanto del punto in se.

La
linea unidimensionale
"A" può essere descritta da un numero, che descrive la lunghezza della linea. La lunghezza può essere misurata dentro un certo numero di unità (pollici, centimetri, larghezze della barretta, ecc...). Questo è misurato in pixel.

Il
rettangolo bi - Dimensionale
Il
rettangolo può essere descritto da due numeri. Un numero è la
lunghezza (la prima linea) e l'altra è l'altezza. Moltiplicando questi
due numeri, potete trovare la zona del rettangolo.
lunghezza x altezza = area
100 x
50 pixel = 5.000 pixel quadrati (o pixels2).

La
scatola tri - Dimensionale
Questa scatola può essere descritta da tre numeri: lunghezza, altezza e profondità. Moltiplicando questi tre numeri, potete trovare il volume della scatola.
Lunghezza
x
larghezza x profondità = volume
10 x 20 pixel x 55 pixel = 125.000
pixel cubici (o pixels3)
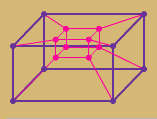
L'
hypercubo quadri - Dimensionale
L' Hypercubo "A" è generato tirando la scatola in una quarta
dimensione -- in uno spazio che non possiamo percepire. È difficile
da immaginare un oggetto four-dimensional (e descrivere uno sulla superficie
bidimensionale di uno schermo del calcolatore), ma in questo caso concentra
la vostra attenzione sulla matematica in questione. La formula (espressione?)
sotto descrive il volume totale (hypervolume) di un oggetto che esiste in
quattro dimensioni spaziali.
lunghezza x altezza x profondità x hyperdepth = iper pixel del volume
10 x 20 pixel x 15 pixel x 60 pixel = 7.500.000 pixels4

È
questa una formula matematica...... espressiva?
Anche se è difficile da immaginare un oggetto four-dimensional, il risultante "pixels4" dell'equazione è espressivo. Se ci fosse un'altra scatola four-dimensional appena come quella indicata qui, ma fosse più profondo nella quarta dimensione, l'iper misura del volume dell'oggetto sarebbe più grande. Questo numero sarebbe utile per confrontare "il formato" dell'oggetto a quello di un altro.
Inoltre, per la matematica, in base alla teoria della stringa, è espressivo anche se gli oggetti che descrive sono molto più complessi e molto più difficili da immaginare. È indicato qui un tentativo. Ciò è una rappresentazione approssimativa di cosiddetta figura di Calabi-Yau. Le relative sei dimensioni, con la tridimensionalità spaziale e la dimensione di tempo, rappresentano le 10 dimensioni della teoria della stringa.
