Internet: una passeggiata tra le materie 
(di Furio Petrossi)  

Matematica 

Vedi anche 
Ambienti interattivi: 
Figure Cabri  

Ogni mercoledì compro La Stampa, per il suo inserto Tuttoscienze (il miglior foglio divulgativo settimanale di scienza: sto cercando di far interessare i ragazzi del mio Liceo Scientifico Marinelli ai temi scientifici in generale, al di là della materia che insegno). 

Nel numero del 19 febbraio, in quarta pagina mi sorprende un articolo su una costruzione geometrica fatta da Dave e Dan, quattordici anni, per dividere un segmento in parti uguali: ( l'articolo non e' più on-line, ma puo' essere recuperato sul CD-ROM di Tuttoscienze). 
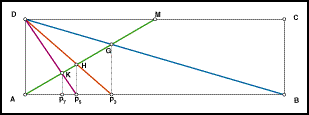
Citando Tuttoscienze "Dopo vari tentativi, avevano trovato una costruzione che permetteva di dividere un segmento in tre parti uguali, determinando il punto P3 ed erano arrivati alle due costruzioni riportate in figura, valide, la prima, per la suddivisione di un segmento in un numero dispari di parti e la seconda, per la suddivisione in un numero pari di parti. Sono costruzioni molto semplici. Si tenga presente che i rettangoli hanno altezza qualsiasi e che la base è il segmento AB che si vuole suddividere in parti uguali. Non sarà poi difficile scoprire l'algoritmo con cui sono stati costruiti i punti P3, P5, P7...". 

Devo dire che ho provato con poco successo di ottenere una dimostrazione dagli studenti della quarta liceo... 

Per risolvere il problema Dave e Dan avevano lavorato due ore al computer, utilizzando un programma di geometria molto diffuso negli Stati Uniti, il Geometer's Sketchpad. 

Mi hanno incuriosito i riferimenti bibliografici dati da Tuttoscienze: si tratta di http: //www.nctm. org e del sito della scuola di Westport: http: //www.academy.org/GLaD/. Il secondo collegamento proprio non funziona: mi porta all' Academy of Motion Picture Arts and Sciences ma il collegamento non c'è perché si sono sbagliati: si tratta della Greens Farms Academy e la storia intera si trova in http://www.gfacademy.org/GLaD/index.html. Il primo link è stato scritto invece con uno o due spazi di troppo, si tratta di http://www.nctm.org/ e corrisponde al National Council of Teachers of Mathematics, un bel punto di partenza per chi, sapendo l'inglese, vuole vedere cosa c'è di matematica per l'insegnamento su Internet (The Internet come dicono nei paesi anglosassoni). Se volete vedere la dimostrazione geometrica della soluzione, vedetela in http://www.nctm.org/journals/MT/mt_1997/articles/euclid/page_3.htm. 

Come possiamo vedere, passeggiando nella matematica, spesso quello che si può trovare in Internet non è esplicitamente curriculare, almeno per noi in Italia. Non che manchino schemi e proposte di lavoro curriculare all'estero (collegatevi a  e partite...), ne mancano in Italia. 

Ci sono, per le risorse didattiche italiane, alcuni indici di ricerca generale: tra essi ricordo The World-Wide Web Virtual Library: The Italian General Subject Tree, tenuto dal CNR di Milano, alla voce Didattica, manca però ancora il materiale: c'è ancora poco interesse da parte delle Associazioni di Insegnanti (UMI ad esempio). 

E pensare che in america l'associazione degli insegnanti (The National Science Teachers Association) - in effetti sponsorizzata dalla Microsoft Corporation, non dalla Olivetti o dalla Cassa di Risparmio - ha delle pagine molto belle, suggerimenti per schemi di lezioni ecc. . 

In Italia ho trovato interessante la mostra "OLTRE IL COMPASSO, La Geometria delle curve" organizzata dalla Scuola Normale Superiore di Pisa: si apre qui il discorso dei Musei Virtuali, una delle cose più interessanti che può dare Internet all'insegnamento. Date un'occhiata anche al Museo Universitario di Storia Naturale e della Strumentazione Scientifica
Università degli studi di Modena e Reggio Emilia.

Oops! Mi è scappato Insegnamento: sto andando fuori tendenza. L'Europa pensa che ora l'accento debba essere posto sull'Apprendimento, su un processo centrato su chi sta costruendo il proprio sapere, il proprio presente e futuro. Un apprendimento che non finisca con la scuola ma prosegua nel corso dell'intera vita. 

L'educazione alle tecnologie non si dissocia allora da una educazione allo sviluppo delle proprie abilità di scegliere le occasioni formative che vengono offerte, all'autonomia nello studio. 

Prima di abbandonare il discorso della matematica vale la pena di mostrare un bell'esempio di lezione di lezione di geometria proiettiva applicata al cinema, si tratta di "Vectors and Velociraptors" ed è una pagina segnalata dallo Scientific American all'interno di un articolo sui dinosauri... ovviamente in inglese! 

Non dimenticate anche la "Gallery of Interactive Geometry", un posto carino. 

 

(Orientamento alla matematica)