Calcolo di superfici
introduzione
Il calcolo di superfici non risulta sempre agevole, sia perché molti oggetti non regolari non si possono "schiacciare"
su un foglio di carta per disegnarne la superficie, sia perché lo strumento che misura le superficie chiamato planimetro,
necessita della mano dell'uomo, è uno strumento non troppo comune e non direttamente utilizzabile.
A questi mezzi oggigiorno c'è l'appoggio informatico che attraverso alcune opzioni in alcuni programmi è agevolmente in
grado di calcolare superfici, ma tale applicazione, molto utile in grafica, non si rapporta in maniera diretta con il mondo
reale dove anche piccole differenze possono causare misure inutili.
il planimetro
Il planimetro è uno strumento che serve per misurare l'area di superfici piane delimitate da un contorno chiuso.
Il planimetro risolve quindi meccanicamente un problema di calcolo (calcolo integrale) altrimenti non facilmente
risolvibile manualmente.
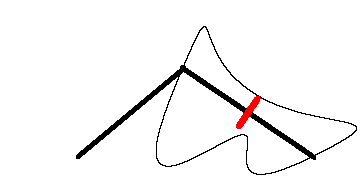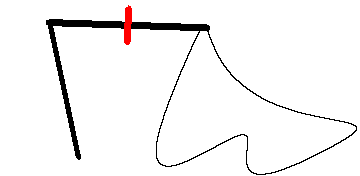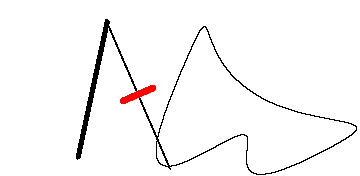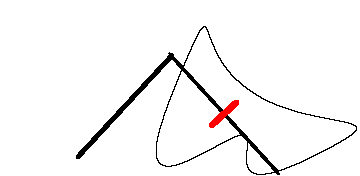
Esistono diversi tipi di planimetro; i principali sono il planimetro lineare ed il planimetro polare, che servono
per calcolare le aree di superfici piane, il planimetro sferico con il quale si determina l'area di una superficie
sferica (geometria ellittica quindi non geometria Euclidea).
l'uso di carta quadrettata
Il metodo più a portata di mano per calcolare superifici di figure irregolari, rimane l'utilizzo di carta quadrettata
sulla quale riportare il contorno dell'oggeto di cui si vuole calcolare la superficie. Per una figura a contorno
curvilinea, come un cerchio, è possibile operare con la conta dei quadretti completamente interni alla figura e il
calcolo dei quadretti di contorno.
Una media dei quadretti inscritti e dei quadretti circoscritti alla figura dà
in genere una buona stima della figura in esame qui in scala 1:2 e 1:1.
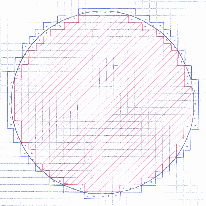 
Come si potrà osservare il centro non si trova in un punto preciso per cui il conteggio dei quadretti non può far uso
di specifici elementi di simmetria, si vanno quindi a contare tutti i quadretti interni e poi i quadretti del contorno
con i seguenti risultati:
| quadretto 5 mm x 5 mm | n° quadretti | area |
| quadretti interni (in rosso) | 483 | 120,75 cm2 |
| quadretti del contorno (in blu) | 089 | 022,25 cm2 |
| quadretti totali interno + contorno | 572 | 143,00 cm2 |
| stima del cerchio (483 + 572)/2 | 527,5 | 131,875 cm2 |
La stima si avvicina abbastanza bene all'area del cerchio reale che avendo un raggio di 6,5 cm possiede un'area di
pi greco * (6,5)2 = 3,141592... * 42,25 = 132,732...
con un errore tra la stima e la misura reale del 6,5 per mille quindi inferiore all'1%.
Bibliografia
Enciclopedia di scienza e tecnica ed. Curcio 1976
Bagatti Franco, Corradi Elis, Desco Alessandro e Ropa Claudia "Conoscere la materia" ed. Zanichelli 2007
|