I modelli atomici a orbitali
introduzione
Senza scartare il modello di E. Rutherford che risultava corretto per numerose osservazioni
gli scienziati cominciano a cercare idee per poter "stabilizzare" le orbite degli elettroni
attorno al nucleo. Infatti secondo le leggi delal fisica classica un sistema a due corpi che
si attraggono tra di loro non può essere eternamente stabile.
Per esempio la Luna si allontana dalla Terra ogni anno di pochi centimetri, ne segue che nel sistema
Terra-Luna la prima perde energia (di rotazione) a favore della seconda.
Tutta una serie di osservazioni tra il 1911 ed il 1925 compiute da importanti scienziati quali
N. Bohr, A. Einstein e A. Sommerfeld, Landé, W. Pauli mireranno a questo obiettivo.
Il primo conflitto mondiale (1914-1918) non farà che rallentare il raggiungimento di tale obiettivo
ed è solo nel 1926 che si arriva alla stesura della quantomeccanica (per opera di M. Planck,
N. Bohr, W. Heisenberg, E. Schrödinger, M. Born, W. Pauli, E. Fermi, ed il principe L. V. de Broglie)
che riuscirà a spiegare in termini fisico-matematici la stabilità del modello nucleare
di Rutherford.
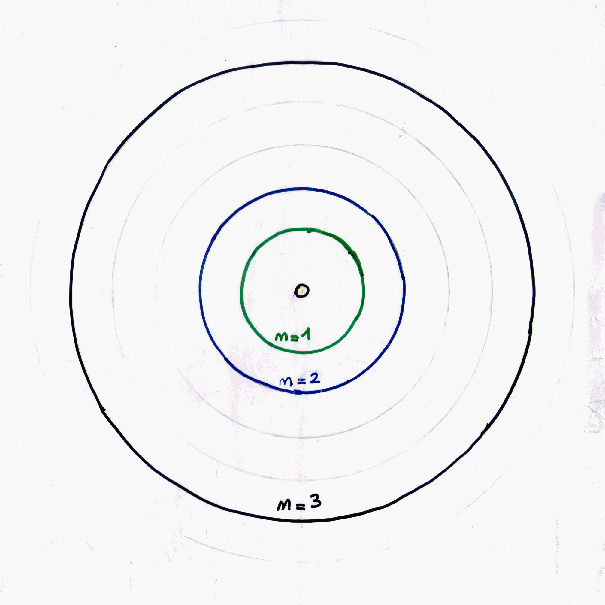
1913 il modello di Bohr (un numero quantico)
Per spiegare la stabilità degli atomi nel modello di Rutherford, Niels Bohr ipotizzò
che gli elettroni non si muovessero lungo orbite di tipo planetario ma in sfere attorno al nucleo
a ben determinate distanze da questo.
Introdusse quindi il concetto di orbitale, ossia una zona dello spazio che l'elettrone è
libero di ovccupare e dove può muoversi senza perdere energia. Ai vari orbitali diede
un numero naturale che chiamò quantico principale, che si poteva, per quanto detto,
interpretare come la distanza a cui si posizionano gli elettroni al di fuori del nucleo. Il numero
principale venne poi indicato con la lettera n.
Si sapeva dal 1885 che le transizioni nella spettroscopia dell'idrogeno avvenivano secondo
relazioni ben precise che rispettavano la semplice formula empirica, scoperta appunto dallo
spettroscopista Balmer:
frequenza di eccitazione=R • c • (1/n22 - 1/n12)
in cui R è detta costante di Rydberg con il valore di 109678 cm-1, c è
la velocità della luce n2 può variare da 1 a 5, e si ha sempre
n2 > n1.
Bohr riprese quindi la formula di Balmer dandogli un significato fisico coerente con il modello
atomico che stava disegnando.
Il valore del numero quantico principale n varia da 1 a infinito secondo la normale successione
dei numeri naturali cioé:
1, 2, 3, 4, 5, 6, ...
Transizioni tra un livello energetico e l'altro è stato confermato, sono il principio base della
spettroscopia atomica sulla quale si basano molti strumenti analitici per la determinazione
di ioni e metalli in campioni liquidi o gassosi.
1916 il modello di Bohr-Sommerfeld (due numeri quantici)
Sfortunatamante il modello di Bohr così eccellente per l'atomo di idrogeno non poteva applicarsi
agli altri atomi con più elettroni.
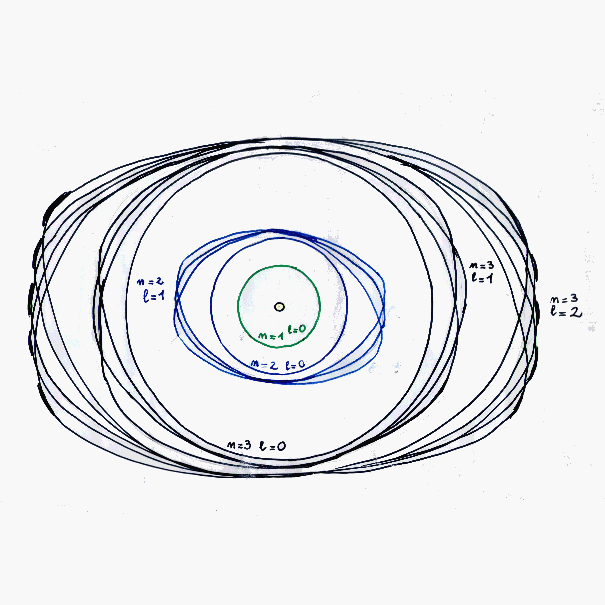
Gli studi di Arnold Sommerfeld (1868-1951) permisero quindi di
introdurre al modello di Bohr un secondo numero quantico indicato con la lettera l e chiamato
secondo numero quantico, o sottolivello energetico, o ellitticità che aveva una influenza di
secondo ordine nelle transizioni o eccitazioni elettroniche tra un livello e l'altro.
Il valore di l si scoprì essere variabile da 0 a n-1 per ogni livello energetico definito
da Bohr, secondo la normale successione dei numeri naturali comprendenti lo zero.
l = 0 nel primo livello per n=1
l = 0 oppure 1 nel secondo livello per n=2
l = 0, 1 o 2 nel terzo livello per n=3
e così via. Quindi l ripetendo quanto già indicato può valere:
0, 1, 2, 3, 4, 5, ..., n-1
Ogni orbitale quindi veniva momentaneamente ad essere individuato da una coppia di valori ( n , l )
che furono detti livello e sottolivello energetico.
Il secondo numero quantico si interpreta quindi anche come forma degli orbitali, più è
alto più l'orbitale assume una forma complessa secondo le simmetrie derivanti dalle funzioni
aritmetiche delle armoniche sferiche.
1919 il modello di Bohr-Sommerfeld (tre numeri quantici)
L'utilizzo di elettromagneti sempre più potenti permise di osservare le transizini elettroniche
sotto l'azione di un campo magnetico.
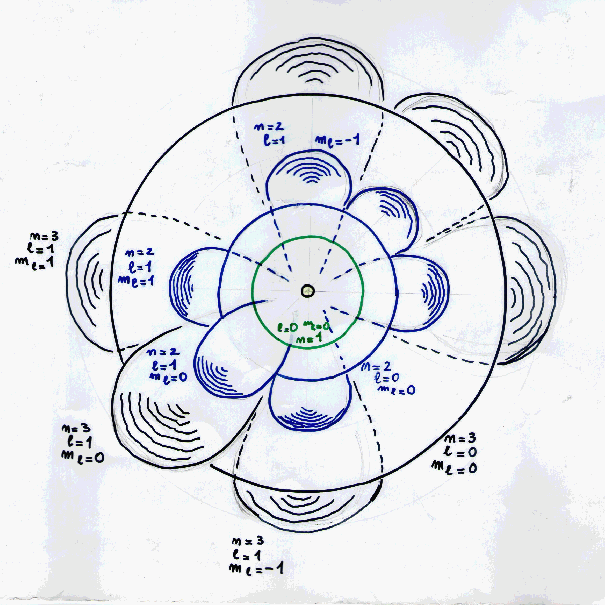
Dapprima si osservarono piccole fluttuazioni sperimentalmente
poco significative. Ma con l'utilizzo di elettromagneti sempre più potenti si riuscirono ad
evidenziare queste differenze che risultarono in numero caratteristico.
Alla luce di queste nuove scoperte il modello a due numeri quantici si rivelò insufficiente
con la necessità da parte dei medesimi scienziati di introdurre una correzione nella forma di
un terzo numero quantico che fu definito per l'appunto terzo numero quantico o numero quantico magnetico
(da cui la lettera m) o direzione degli orbitali. Gli fu attribuito il simbolo ml o,
semplicemente, m.
Il valore di ml si scoprì essere variabile da - l a + l secondo
la normale successione dei numeri interi comprendenti lo zero, cioé:
-l, -l+1, -l+2, ..., -2, -1, 0, +1, +2, ..., +l-2, +l-1, +l
Ogni orbitale veniva quindi ad essere individuato ora da una terna di valori ( n , l , ml ).
1920 il modello di Bohr-Sommerfeld-Landé-Pauli (quattro numeri quantico)
L'utilizzo di elettromagneti sempre più potenti (ed è proprio il caso di ripetersi)
permise risolvere i raggi beta in due tipi aventi una piccolissima variazione di campo magnetico
(effetto Zeeman).
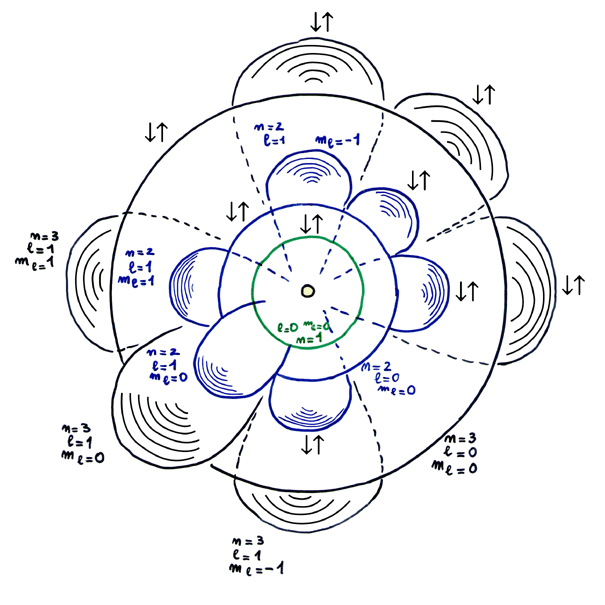
Il fenomeno fu interpretato correttamente da Landé e Wolfgang Pauli come un campo magnetico
proprio posseduto dagli elettroni sia dentro che fuori dall'atomo detto spin.
Werner Heisenberg, all'epoca giovane studente propose l'esistenza di valori di spin semiintero, idea
subito rigettata come assurda dai suoi docenti «nella fisica quantistica non ci sono mezzi valori»;
in realtà sono le transizioni ad avvenire tra unità discrete e non i singoli valori infatti:
ΔE = +½ - (-½) = 1 o anche ΔE = -½ - (+½) = -1.
La medesima idea fu invece sviluppata e portata a compimento, anche in termini di formalismo matematico
(facendo ricorso alle matrici 2x2), da Landé e Pauli.
Il quarto numero quantico, caratteristico degli elettroni, e non degli orbitali per quanto detto, si indica
con il simbolo ms o semplicemente s e ammette i soli valori +½ e -½.
Ogni elettrone in un atomo viene quindi ad essere individuato da una quaterna di valori
( n , l , ml, ms ).
In altri termini è possibile eccitare un elettrone può da uno stato di spin all'altro
sotto l'azione di una opportuna radiazione energetica (nel campo delle deboli microonde o MO).
Questo è il principio su cui funziona la spettroscopia spin elettrone (in inglese Spin
Electron Resonance o E.S.R.).
Bibliografia
AA.VV. Enciclopedia di Sicenza e Tecnica ed. Curcio 1976
Adolfo Ferrari "Trattato di chimica generale ed inorganica" ed. Riccardo Pàtron, Bologna 1965
G. Valitutti, A. Tifi, A. Gentile "La chimica in moduli" ed. Zanichelli
|