Mentre Hardy e Littlewood si facevano strada a fatica attraverso lo strano paesaggio di Riemann, a cinquemila miglia di distanza, negli uffici della capitaneria di porto di Madras, in India, un giovane impiegato di nome Srinivasa Ramanujan aveva sviluppato un'ossessione per il mistero inebriante del flusso irregolare dei numeri primi. Invece di occuparsi del compito tedioso di tenere i registri contabili, per il quale era stato assunto, egli passava tutte le ore di veglia a riempire quaderni di osservazioni e calcoli alla ricerca di ciò che dettava il ritmo a quegli strani numeri. Ramanujan contava i numeri primi senza avere alcuna nozione della sofisticata prospettiva che era stata elaborata in Occidente.
Privo di un'istruzione formale, non aveva il rispetto reverenziale che mostravano Hardy e Littlewood nei confronti della teoria dei numeri e dei numeri primi in particolare, che Hardy definiva «il più difficile di tutti i rami della matematica pura». Svincolato da ogni tradizione matematica, Ramanujan si tuffò nei numeri primi con un entusiasmo quasi infantile. Il suo candore, combinato con una straordinaria predisposizione naturale per la matematica, si sarebbe rivelato la sua grande forza. A Cambridge, Hardy e Littlewood studiavano avidamente la meravigliosa storia sui numeri primi che si dipanava nel libro di Landau.
In India, l'ossessione di Ramanujan per i primi era stata ispirata da un libro molto più elementare, e con conseguenze di portata altrettanto vasta. Ci sono alcuni punti di svolta nella vita di un giovane scienziato che spesso è possibile identificare come fondamentali per il loro sviluppo futuro. Per Riemann fu il libro di Legendre che gli era stato donato quand'era uno scolaro. Quel libro piantò il seme che sarebbe germogliato in una fase successiva della sua vita. Per Hardy e Litdewood, il libro di Landau ebbe un'influenza altrettanto forte.
Nel 1903, all'età di quindici anni, Ramanujan era stato ispirato dalla scoperta di una copia di "A Synopsis of Elementary Results in Pure and Applied Mathematics" di George Carr. Salvo che per il legame con Ramanujan, il libro di Carr e la vita del suo autore hanno scarsa importanza, ma per Ramanujan fu importante il modo in cui quel libro era strutturato. Era un elenco di circa 4.400 classici risultati matematici; solo i risultati, senza dimostrazioni. Ramanujan raccolse la sfida e trascorse gli anni seguenti a studiare a fondo il libro e a spiegare ciascuna delle asserzioni che esso riportava. Avendo ben poca familiarità con lo stile occidentale di dimostrazione, Ramanujan fu costretto a creare una propria matematica. Il fatto di non essere ingabbiato nella camicia di forza dei modi di pensiero convenzionali gli dava la libertà di muoversi a proprio piacimento. E non ci volle molto perché i suoi quaderni si riempissero di idee e risultati che nel libro di Carr non comparivano.
Eulero si era fatto le ossa su molte delle asserzioni non dìmostrate di Fermat. Nell'approccio di Ramanujan ai problemi matematici possiamo riconoscere lo stesso spirito di Eulero. Possedeva una capacità fantastica di intuire come girare e rigirare le formule finché non emergevano nuove prospettive. Fu molto eccitato quando scoprì per proprio conto il collegamento fornito dai numeri immaginari fra la funzione esponenziale e le equazioni che descrivono le onde sonore. Ma la gioia si trasformò in disperazione quando, pochi giorni dopo, il giovane impiegato indiano scoprì che Eulero l'aveva preceduto di centocinquantanni circa. Umiliato e avvilito, Ramanujan nascose i suoi calcoli sotto il soffitto di casa.
Nel migliore dei casi comprendere in che cosa consista la creatività matematica è difficile, ma il modo in cui procedeva Ramanujan ebbe sempre qualcosa di misterioso. Sosteneva che le idee gli venivano portate in sogno dalla dea Namagiri, protettrice della sua famiglia e consorte di Narasìmha, il dio Icone, quarta incarnazione di Vishnu. Altri nel villaggio di Ramanujan credevano che la dea avesse il potere di esorcizzare i demoni. Per Ramanujan Namagiri era la spiegazione dei lampi d'illuminazione che innescavano il suo flusso ininterrotto di scoperte matematiche.
Hadamard, che si era fatto un nome dimostrando il teorema dei numeri primi, era affascinato da ciò che si verifica nella mente di un matematico creativo. Mise le sue idee per iscritto in un libro intitolato La psicologia dell'invenzione in campo matematico, pubblicato nel 1945, in cui avanza tesi persuasive sul ruolo del subconscio. Oggi i neurologi si stanno interessando sempre più ai meccanismi deliamente matematica, dato che potrebbero far luce sul funzionamento del cervello. Spesso sono i periodi di riposo o addirittura di sogno a concedere alla nostra mente la libertà di giocare con idee che si sono impiantate nel cervello durante un'attività intellettiva conscia.
Nel suo libro Hadamard divideva l'atto della scoperta matematica in quattro stadi: preparazione, incubazione, illuminazione e verifica. Se Ramanujan aveva un dono naturale per il terzo di questi stadi, era decisamente carente nel quarto. La sola illuminazione gli era sufficiente, ma non riusciva proprio a cogliere l'importanza della verifica. Forse era il fatto di non essere assillato dalla responsabilità della dimostrazione a concedergli la libertà di scoprire nuovi percorsi nella landa selvaggia della matematica. Il suo stile intuitivo era totalmente in contrasto con le tradizioni scientifiche dell'Occidente. Come scrisse in seguito Littlewood, «un'idea ben chiara di quello che s'intende per dimostrazione non la possedeva affatto; se dal totale miscuglio di indizi e d'intuizione traeva una certezza, non cercava oltre».
Le scuole indiane dovevano molto alle idee introdotte dall'Impero britannico. Tuttavia, il sistema didattico inglese
che era stato tanto utile a Hardy e a Littlewood non fu di alcun aiuto al giovane Ramanujan in India. Nel 1907, mentre la dissertazione di Littlewood riceveva un'accoglienza calorosa a Cambridge, Ramanujan falliva per la terza e definitiva volta gli esami di ammissione al college. Avrebbe certamente superato quegli esami se avessero riguardato soltanto la matematica, ma gli era richiesto anche lo studio dell'inglese, della storia, del sanscrito e persino della fisiologia. Bramino osservante, Ramanujan era rigorosamente vegetariano, e per lui anatomizzare rane e conigli era intollerabile. Ma la bocciatura, benché significasse che non avrebbe potuto iscriversi all'università di Madras, non estinse il fuoco matematico che bruciava dentro di lui.
Nel 1910 Ramanujan era ormai impaziente che le sue idee ricevessero una qualche forma di riconoscimento. In particolare, era eccitato dalla scoperta dì una formula che sembrava fornire un conteggio straordinariamente preciso dei numeri primi. Da principio aveva sperimentato la frustrazione che quasi tutti provano quando tentano di addomesticare questa sequenza selvaggia di numeri. Ma Ramanujan sapeva quanto fossero fondamentali i numeri primi per la matematica e non abbandonò la convinzione che dovesse esistere una formula in grado di spiegarli. Credeva ancora, ingenuamente, che tutta la matematica e le sue strutture si potessero esprimere con esattezza per mezzo di equazioni e formule. Come ebbe a dire in seguito Littlewood, «quale grande matematico avrebbe potuto essere Ramanujan cento o centocinquant'anni fa? Che cosa sarebbe accaduto se fosse entrato in contatto con Eulero al momento giusto? Ma il grande periodo delle formule sembra ormai passato». Ramanujan, tuttavia, non era stato esposto al cambiamento dì prospettiva indotto da Riemann. Era determinato a trovare una formula che producesse i numeri primi. Ed era ansioso di spiegare ciò che aveva scoperto fino ad allora a qualcuno che potesse apprezzare le sue idee.
L'impressione che suscitavano i suoi quaderni e l'influenza della rete braminica gli avevano garantito un impiego come contabile alla capitaneria di porto di Madras. Aveva anche cominciato a pubblicare alcune delle sue idee sul «Journal of the Indian Mathematical Society», e ormai il suo nome era giunto all'attenzione delle autorità britannìche. C.L.T. Griffith, che lavorava all'Istituto di ingegneria di Madras, riconobbe che l'opera di Ramanujan era quella di un «matematico notevole», ma non si sentiva in grado dì seguirla o di criticarla. Decise perciò di richiedere l'opinione di uno dei professori che gli avevano insegnato matematica quand'era studente a Londra.
Privo di una preparazione formale, Ramanujan aveva elaborato uno stile matematico molto personale. Non è dunque sorprendente che, quando il professor Hill dello University College di Londra ricevette le carte in cui Ramanujan sosteneva dì aver dimostrato che
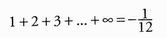
ne liquidò buona parte come prive di senso. Persine a un occhio non qualificato questa formula appare ridicola. Sommare tutti i numeri interi e ottenere come risultato una frazione negativa è chiaramente l'opera di un pazzo! «Il signor Ramanujan è caduto nelle trappole del tema piuttosto difficile delle serie divergenti» scrìsse il professore a Griffith.
Tuttavia, il giudizio dì Hill non era totalmente negativo. Incoraggiato dai commenti che gli furono riferiti, Ramanujan decìse di tentare la sorte e dì scrivere direttamente a un certo numero di matematici di Cambridge. Due dei destinatati non riuscirono a penetrare il messaggio celato dietro la strana aritmetica di Ramanujan e declinarono la sua richiesta d'aiuto. Ma poi la lettera di Ramanujan arrivò sulla scrivania di Hardy.
La matematica sembra avere il potere di portare allo scoperto gli eccentrici. E forse una parte della responsabilità è da attribuire a Fermat. La lettera prestampata di rifiuto ideata da Landau testimonia di quante risposte assurde egli ricevesse da individui che rivendicavano il diritto a reclamare il premio Wolfskehl per aver risolto l'ultimo teorema di Fermat. I matematici sono abituati a ricevere lettere non richieste piene dì folli teorie numerologiche. Hardy, per esempio, aveva fatto l'abitudine a venir sommerso da un diluvio di manoscritti i cui autori, come ricordava il suo amico C.P. Snow, affermavano di aver risolto i misteri profetici della Grande piramide o decifrato i crittogrammi che Francesco Bacone aveva celato nei drammi di Shakespeare.
Di recente Ramanujan aveva ricevuto una copia del libro di Hardy "Orders of lnfinity" da Ganapathy Iyer, un professore di matematica dì Madras con cui trascorreva le serate a di scutere dì matematica sulla spiaggia. Mentre leggeva Hardy, Ramanujan dovette rendersi conto di aver trovato finalmente qualcuno che avrebbe potuto apprezzare le sue idee, ma in seguito ammise di aver temuto che le sue somme infinite avrebbero indotto Hardy «a farmi notare che la mia destinazione era il manicomio». C'era un'affermazione dì Hardy che eccitava in modo particolare Ramanujan: «A oggi non è stata trovata un'espressione definita che fornisca il numero di numeri primi minori di un qualsiasi numero dato». Ramanujan aveva scoperto un'espressione che pensava catturasse quel numero con una precisione pressoché assoluta, e aveva un gran desiderio di scoprire che cosa pensasse Hardy della sua formula.
L'impressione immediata che ebbe Hardy quando trovò fra la posta del mattino la grossa busta di Ramanujan coperta di francobolli indiani non fu favorevole. Dentro c'era un manoscritto pieno dì teoremi bizzarri, deliranti, sul conteggio dei numeri primi, insieme a risultati ben noti presentati come se fossero scoperte originali. Nella lettera di accompagnamento Ramanujan dichiarava di aver «trovato una funzione che dà una rappresentazione esatta del numero di numeri primi». Hardy sapeva che quella era un'affermazione sbalorditiva, ma nel manoscritto non compariva nessuna formula. Peggio ancora, non si dimostrava nulla! Per Hardy, la dimostrazione era tutto. Una volta, conversando con Bertrand Russell alla Tavola alta del Trinity College, disse: «Se io riuscissi a dimostrare con la logica che tu morirai entro cinque minuti, sarei addolorato per la tua morte imminente, ma il mio dolore sarebbe molto mitigato dal piacere della dimostrazione».
Secondo C.R Snow, dopo aver dato una scorsa veloce al lavoro di Ramanujan, Hardy «non era solo annoiato, ma anche irritato. Sembrava che fosse una sorta di curioso imbroglio». Ma prima di sera quei folli teoremi cominciarono a esercitare la loro malia e Hardy convocò Littlewood per discuterne dopo cena. Per mezzanotte ne erano venuti a capo. Armati delle conoscenze necessarie per decifrare il linguaggio non convenzionale di Ramanujan, ora Hardy e Littlewood si rendevano conto che quelle non erano le esternazioni di uno spostato ma l'opera di un genio, di un matematico privo di una preparazione formale ma senza alcun dubbio brillante.
Entrambi compresero che la somma infinita apparentemente insensata di Ramanujan altro non era se non la riscoperta del metodo per definire la parte mancante del paesaggio zeta di Riemann. La chiave per decodificare la formula di Ramanujan è esprimere il numero 2 come 1/2-1 (2-1 è un altro modo di scrìvere 1/2). Applicando lo stesso trucco a ogni numero della somma infinita, Hardy e Littlewood riscrissero la formula di Ramanujan nella forma seguente:
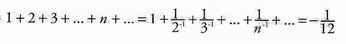
Quella che sì trovavano davanti era la soluzione di Riemann per Ìl calcolo della funzione zeta quando vi si inseriva il numero —1. Senza un'istruzione formale, Ramanujan aveva compiuto l'intero percorso da solo e aveva ricostruito la scoperta del paesaggio zeta compiuta da Riemann.
La lettera di Ramanujan non avrebbe potuto giungere in un momento migliore. Grazie al libro di Landau, Littlewood e Hardy si erano lasciati affascinare dalle meraviglie della funzione zeta di Riemann e delle sue connessioni con i numeri primi. Ed ecco che Ramanujan sosteneva di avere una formula incredibilmente precisa per calcolare il numero dei numeri primi entro un qualsiasi intervallo numerico dato. Quella stessa mattina Hardy aveva respinto quell'affermazione, convinto che Ramanujan fosse uno dei tanti spostati che si dedicavano alla matematica. Ma il lavoro serale aveva posto quella busta proveniente dall'India in una luce completamente diversa.
Hardy e Littlewood dovettero rimanere di sasso di fronte all'affermazione di Ramanujan secondo cui la sua formula permetteva di calcolare il numero di numeri primi fino a 100.000.000 «in genere senza alcun errore e ìn alcuni casi con un errore di 1 o di 2».
Il problema era che non veniva fornita alcuna formula. In effetti, tutta quanta la lettera era profondamente frustrante per i due matematici, dato che per loro una dimostrazione era assolutamente fondamentale. Le formule e le asserzioni che riempivano la lettera, invece, non venivano mai giustificate, né veniva spiegato da dove arrivassero.
Hardy rispose a Ramanujan in termini molto positivi, pregandolo di inviare delle dimostrazioni e maggiori dettagli sulle formule relative ai numeri primi. Littlewood aggiunse una nota per chiedere che fosse spedita la formula per i numeri primi e «quanta più dimostrazione possibile senza indugi». I due marematici fremevano in previsione della risposta di Ramanujan. Trascorsero molte cene alla Tavola alta cercando di decifrare altre parri della sua prima lettera. Bertrand Russell scrisse a un amico di aver trovato «nella Hall Hardy e Littlewood in uno stato di grande agitazione, perché ritenevano di aver scoperto un secondo Newton, un impiegato indù di Madras con uno stipendio di 20 sterline all'anno».
Puntuale arrivò una seconda lettera di Ramanujan. Conteneva varie formule per calcolare il numero dei numeri primi ma era ancora priva di dimostrazioni. «Com'è esasperante la sua lettera a causa di ciò» scrisse Littlewood, e proseguì ipotizzando che forse Ramanujan temeva che Hardy avesse intenzione di sottrargli le sue scoperte. Studiando questa seconda lettera, Hardy e Littlewood scoprirono che Ramanujan aveva concepito un'altra delle scoperte fondamentali di Riemann. Il perfezionamento della formula di Gauss per il conteggio dei numeri primi introdotto da Riemann era molto preciso, e inoltre Riemann aveva scoperto come usare gli zeri del paesaggio zeta per eliminare gli errori che la sua formula ancora produceva. Letteralmente dal nulla Ramanujan aveva ricostruito una parte della formula ideata da Riemann cinquant'anni prima. La formula di Ramanujan comprendeva Ìl perfezionamento di Riemann della stima del numero dei primi data da Gauss, ma non le correzioni che Riemann aveva ottenuto utilizzando gli zeri del suo paesaggio.
Ramanujan stava forse dicendo che gli errori prodotti dai punti a livello del mare si cancellavano a vicenda in modo miracoloso? Fourier aveva fornito un interprelazione musicale di quegli errori. Ciascuno zero è come un diapason, e quando vibrano tutti insieme questi diapason creano il suono dei numeri primi. Talvolta le onde sonore possono combinarsi per produrre il silenzio se si cancellano a vicenda. In un aeroplano sì riduce il frastuono dei motori creando delle onde sonore all'interno della cabina per contrastarlo. Ramanujan stava forse affermando che le onde di Riemann dovute agli zeri avrebbero potuto produrre silenzio?
Durante le vacanze di Pasqua, Littlewood partì per la CornovagHa insieme all'amante e alla famiglia di lei portando con sé una copia della lettera di Ramanujan. «Caro Hardy» scrisse {i due non si chiamavano mai l'un l'altro per nome di battesimo) «la faccenda dei numeri primi è sbagliata.» Littlewood era riuscito a dimostrare che in nessun modo gli errori dovuti a quelle onde avrebbero potuto cancellarsi a vicenda per giustificare ciò che affermava Ramanujan, e cioè che la sua ricostruzione della formula di Riemann era precisa quanto lui sosteneva. Ci sarebbe sempre stato del rumore, per quanto in là ci si spìngesse a contare.
Si da il caso che l'analisi dì Littlewood stimolata dalla lettera di Ramanujan portò a una nuova intuizione interessante sull'opera compiuta da Riemann. L'ipotesi di Riemann era importante per i matematici perché implicava che la differenza fra la stima di Gauss e il vero numero di numeri primi compresi fra 1 e N sarebbe risultata molto piccola rispetto a N; in sostanza non sarebbe mai stata maggiore della radice quadrata di N, Ma se anche un solo zero non si fosse trovato sulla retta magica di Riemann, allora l'errore sarebbe stato maggiore. Adesso la lettera di Ramanujan sembrava suggerire che era possibile far meglio di Riemann. Poteva darsi che, proseguendo a contare i numeri primi, l'errore sarebbe diventato ancora più piccolo della radice quadrata di N. Il lavoro di Littlewood in Cornovaglia aveva stroncato quella speranza. Littlewood riuscì a dimostrare che in un numero infinito di casi l'errore prodotto dagli zeri sarebbe risultato almeno grande quanto la radice quadrata di N. L'ipotesi di Riemann rappresentava lo scenario ottimale. Ramanujan si era semplicemente sbagliato, ma Hardy rimase comunque impressionato. Come scrisse in seguito, «non sono sicuro che da un certo punto di vista questo suo fallimento non sia stato più meraviglioso di tutti Ì suoi trionfi».
«Ho una vaga teoria riguardo all'origine dei suoi errori.» Nella sua lettera a Hardy, Littlewood ipotizzava che Ramanujan credesse erroneamente che nel paesaggio zeta non ci fossero punti a livello del mare. Se fosse stato effettivamente così, allora in effetti le formule di Ramanujan sarebbero risultate esatte. Ciononostante Littlewood era eccitato. «Posso ritenere che egli sia quanto meno un Jacobi» dichiarò, paragonando Ramanujan a una delle celebrità fra i matematici della generazione di Riemann. Hardy scrisse a Ramanujan: «Aver dimostrato ciò che lei sostiene sarebbe stata l'impresa matematica più straordinaria dell'intera storia della matematica». Era chiaro che, benché traboccasse di talento, Ramanujan aveva un disperato bisogno di essere aggiornato sullo
stato attuale delle conoscenze. Littlewood scrisse a Hardy a proposito della sua intuizione: «Non sorprende che sia finito in trappola, ignaro come presumibilmente è della diabolica malignità Ìnsita nei primi». Come osservò Hardy, «aveva un handicap impossìbile da superare, un indù povero e solitario che si misurava intellettualmente con la saggezza accumulata in Europa».
Sì risolsero a fare tutto quanto fosse necessario per portare Ramanujan a Cambridge. Inviarono in India E.H. Neville, un fellow del Trinity College, affinchè convincesse Ràmanujan a unirsi a loro. Da principio Ramanujan era riluttante a lasciare l'India perché, essendo un bramino osservante, credeva che attraversare i mari avrebbe fatto di lui un paria. Un amico, Narayana Iyer, si rese conto che Ramanujan agognava di andare a Cambridge ed escogitò un piano. lyer era convinto che la devozione di Ramanujan per la matematica e per la dea Namagirì insieme potessero produrre una rivelazione che lo avrebbe persuaso a partire per Cambridge. Lo portò al tempio di Namagiri a cercare ispirazione divina. Dopo tre notti passate a dormire sul pavimento di pietra del tempio, Ramanujan si destò di soprassalto e si affrettò a scuotere l'amico dal sonno. «Ho visto in un lampo dì luce splendente Namagiri che mi ordinava di attraversare ìl mare.» Iyer sorrise. Il suo piano aveva funzionato.
Ramanujan temeva anche che la sua famiglia non fosse d'accordo. Ma Namagìri, la divinità che la proteggeva, doveva intervenire di nuovo. La madre di Ramanujan sognò che suo figlio era seduto in una grande sala circondato da europei e che la dea Namagiri le aveva ordinato di non ostacolarlo. A preoccuparlo, infine, era la prospettiva dì essere sottoposto ad altri esami umilianti quando fosse arrivato a Cambridge. Neville riuscì a dissipare quest'ultimo timore. Ormai tutto era pronto perché Ramanujan lasciasse la caotica distesa di minuscole case che era Madras per gli imponenti saloni e le grandi biblioteche di Cambridge, lo scenario sognato da sua madre.
Nel 1914 Ramanujan arrivò a Cambridge, ed ebbe cosi inizio una delle grandi collaborazioni della storia della matematica. Hardy parlò sempre in modo appassionato del periodo in cui lavorò con Ramanujan. Traevano piacere l'uno dalle idee matematiche dell'altro, lieti di aver trovato uno spìrito affine con il quale condividere il loro amore per i numeri. In seguito Hardy avrebbe ripensato a quegli anni come ad alcuni fra i più felici della sua vita, e avrebbe parlato della relazione con Ramanujan in toni toccanti, definendola «l'unica vicenda romantica della mìa vita».
Il sodalizio di Hardy e Ramanujan faceva pensare alla classica squadra investigativa che conduce un interrogatorio, una squadra in cui c'è un buono e c'è un cattivo. Il buono è l'eterno ottimista pieno di proposte folli. Il cattivo è il pessimista, che dubita di tutto e vede la carta sparire nella manica. Ramanujan aveva bisogno che Hardy il critico tenesse a bada il suo entusiasmo mentre interrogavano il loro sospetto matematico.
Trovare un terreno comune, tuttavìa, non era sempre facile. C'era sicuramente un contrasto culturale. Mentre Hardy e Littlewood pretendevano dimostrazioni rigorose, nello stile occidentale, i teoremi di Ramanujan si riversavano semplicemente fuori, ispirati dalla dea Namagiri. Spesso Hardy e Littlewood non riuscivano proprio a capire da dove uscissero le idee del loro nuovo collega. Hardy osservò: «Sembrava ridicolo angustiarlo domandandogli come avesse scoperto questo o quel problema noto, quando lui me ne mostrava una mezza dozzina dì nuovi quasi ogni giorno».
Ramanujan non doveva vedersela soltanto con lo shock cultural-matematico. Era solo in un mondo alieno fatto di tocchi e toghe nere. Non riusciva a trovare cibo vegetariano e scriveva a casa per farsi spedire pacchi di tamarindo e olio di noci di cocco. Se non ci fosse stato il mondo a lui familiare della matematica, la transizione sì sarebbe probabilmente rivelata impossibile. Neville, il fellow che si era conquistato la sua fiducia in India, descrìsse quei primi giorni: «Soffriva le piccole pene della vita in una civiltà straniera, ìl gusto sgradevole di verdure a cui non era avvezzo, le scarpe che gli tormentavano i piedi che per ventisei anni aveva avuto liberi. Ma era un uomo felice, che trovava gioia nella società matematica in cui stava facendo il suo ingresso». Lo si poteva vedere ogni giorno camminare goffo in ciabatte nel cortile interno del college, avendo rinunciato per disperazione a indossare le sue scarpe inglesi. Ma una volta accomodatosi nell'ufficio di Hardy, Ì suoi quaderni aperti davanti a sé, poteva rifugiarsi nelle sue formule e nelle sue equazioni, mentre Hardy lo fissava, preso nella rete dei suoi magici teoremi. Ramanujan era passato dall'isolamento matematico dell'India alla solitudine culturale di Cambridge, ma aveva guadagnato un compagno con il quale esplorare il suo mondo matematico.
Hardy scoprì che dare un'educazione matematica a Ramanujan era una vera e propria impresa dì equilibrismo. Temeva che se avesse tentato con troppa insistenza di costringere Ramanujan a consumare energie nella dimostrazione dei suoi risultati avrebbe potuto «distruggere la sua fiducia in se stesso o spezzare l'incantesimo della sua ispirazione». Affidò a Littlewood il compito di farlo familiarizzare con il rigore della matematica occidentale. Littlewood scoprì che era un compito virtualmente impossibile. Qualunque cosa egli tentasse di presentare a Ramanujan, otteneva in risposta una valanga di idee originali che lo bloccavano seduta stante.
Benché i tentativi di Ramanujan dì produrre formule esatte per il conteggio dei numeri primi avesse contribuito a far partire la sua nave per l'Inghilterra, fu in campi correlati che alla fine egli lasciò il proprio segno. La lettura dei commenti pessimìstici di Hardy e Littlewood sulla malignità dei numeri primi l'aveva dissuaso dall'affrontarli in modo diretto. Si possono solo fare speculazioni su ciò che Ramanujan avrebbe potuto scoprire se non gli si fosse trasmessa la paura dell'Occidente per i numeri primi.
Insieme a Hardy, comunque, Ramanujan continuò la sua esplorazione di pròprietà dei numeri correlate. Le idee che lui e Hardy elaborarono avrebbero contribuito al primo passo avanti sulla strada di una dimostrazione della congettura di Goldbach, che cioè ogni numero pari è la somma di due numeri primi. Quel progresso giunse per vìa indiretta, ma il suo punto di partenza fu l'ingenua fiducia di Ramanujan nell'esistenza di formule esatte per esprìmere importanti sequenze numeriche come quella dei numeri primi. Nella stessa lettera in cui egli sosteneva dì aver trovato una formula per i numeri primi, affermava dì aver compreso come generare un'altra sequenza rimasta fino ad allora indomata: quella delle partizioni dì un numero intero.
Quanti modi diversi ci sono di dividere cinque pietre in pile distinte? Il numero delle pile varia da un massimo di cinque pile composte da una sola pietra a una sola pila composta da cinque pietre, con un certo numero di possibilità intermedie:
I sette modi possìbili di ripartire cinque pietre.
Tali possibilità distinte sono chiamate le partizioni del numero 5. Come mostra l'illustrazione, esistono sette possibili partizioni di 5.
Ed ecco qual è il numero di partizioni per i numeri interi che vanno da 1 a 15:
Questa è una delle sequenze numeriche che abbiamo incontrato nel capitolo 2. Sono numeri che spuntano nel mondo fisico quasi con la stessa frequenza dei numeri di Fibonacci. Per esempio, dedurre la densità dei livelli energetici in certi sistemi quantistici semplici si riduce a comprendere : il modo in cui cresce il numero delle partizioni.
La distribuzione di questi numeri non appare casuale quanto quella dei numeri primi, ma la generazione dì Hardy aveva quasi rinunciato a trovare una formula esatta che producesse la loro sequenza. I matematici pensavano che, al massimo, vi potesse essere una formula in grado di produrre una stima che non si discostasse molto dall'effettivo numero di partizioni di N, in modo del tutto simile a quello in cui la formula di Gauss per Ì numeri primi forniva una buona approssimazione del numero di numeri primi non maggiori di N. Ma a Ramanujan non era mai stato insegnato a temere quel genere di sequenze. Era decìso a trovare una formula che gli dicesse che esistevano esattamente cinque modi dì dividere quattro pietre in pile distinte, o che ce n'erano 3.972.999.029.388 di divìdere 200 pietre in pile distinte.
Laddove aveva fallito con i numeri primi, Ramanujan ottenne un successo spettacolare con le partizioni. Fu la combinazione della capacità di Hardy di venire a capo di dimostrazioni complesse e della cieca fiducia di Ramanujan nell'esistenza di una formula esatta a condurli alla scoperta. Littlewood non capi mai «perché Ramanujan era così sicuro che ne esistesse una». E quando si osserva la formula — in cui compaiono la radice quadrata di 2,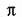 
, differenziali, funzioni trigonometriche, numeri immaginari — non si può fare a meno di domandarsi come sia stata concepita:
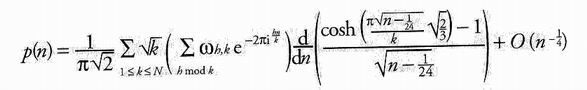
In seguito Littlewood osservò: «Dobbiamo il teorema a una collaborazione eccezionalmente felice fra due uomini dotati di talenti assai dissimili, alla quale ciascuno diede il contributo migliore, più caratteristico e fortunato che possedeva».
Nella vicenda del calcolo delle partizioni c'è un dettaglio curioso. La complicata formula di Hardy e Ramanujan non fornisce il numero esatto di partizioni; produce invece una risposta che è corretta se la si approssima al numero intero più vicino. Così, per esempio, quando nella formula si inserisce il numero 200, si ottiene un valore non intero approssimato a 3.972.999.029.388. Perciò, benché la formula permetta di ottenere la risposta cercata, il fatto che non colga l'essenza dei numeri di partizioni di Noggetti lascia insoddisfatti. (In seguito sarebbe stata scoperta una variante della formula che da la risposta rigorosamente esatta.)
Anche se Ramanujan non riuscì a portare a buon fine lo stesso stratagemma nel caso dei numeri primi, il lavoro che compì insieme a Hardy sulla funzione dì partizione ebbe un impatto importante sulla congettura di Goldbach, uno dei grandi problemi irrisolti della teoria dei numeri primi. La maggior parte dei matematici aveva rinunciato persino a tentare dì risolvere questo problema. Né era mai stata proposta una sola idea da cui partire per provare a fare qualche progresso concreto nella risoluzione. Soltanto qualche anno prima, Landau aveva dichiarato che il problema era semplicemente inattaccabile.
Il lavoro compiuto da Hardy e Ramanujan sulla funzione di partizione inaugurò una tecnica che oggi è chiamata metodo del cerchio dì Hardy e Littlewood. Il riferimento al cerchio nel nome del metodo trae origine dai piccoli diagrammi che accompagnavano i calcoli di Hardy e Ramanujan e che rappresentavano cerchi nella mappa dei numeri immaginati attorno ai quali i due matematici cercavano di eseguire delle integrazioni. Il motivo per il quale al metodo viene associato il nome di Littlewood e non quello di Ramanujan è l'uso che Littlewood e Hardy ne fecero per dare il primo contributo sostanziale a una dimostrazione della congettura di Goldbach. Pur non essendo in grado di provare che ogni numero pari poteva essere espresso come somma di due numeri primi, nel 1923 Hardy e Littlewood riuscirono a dimostrare una cosa che per i matematici era quasi altrettanto importante, ovvero che tutti Ì numeri dìspari maggiori di un certo numero fissato (un numero enorme) potevano essere scritti come somma dì tre numeri primi. Ma c'era una condizione che erano obbligati a porre perché la loro dimostrazione risultasse valida: che l'ipotesi di Riemann fosse vera. Questo era dunque ancora un altro risultato subordinato al fatto che l'ipotesi di Riemann diventasse prima o poi ìl teorema di Riemann.
Ramanujan aveva contribuito a sviluppare quella tecnica, ma malauguratamente non visse abbastanza per essere testimone del ruolo inaspettato che essa ebbe per la matematica. Nel 1917 Ramanujan era sempre più depresso. La Gran Bretagna era stretta nella morsa degli orrori della Prima guerra mondiale. Il Trinity College aveva appena respinto la nomina a fellow di Ramanujan, la fellowship di Russell era stata da poco revocata a causa dei suoi sentimenti antibellici e il college non era disposto a tollerare le posizioni pacifiste di Ramanujan. Benché alla fine avesse imparato a comprìmere i piedi dentro scarpe occidentali e a sfoggiare il tocco e la toga, il suo cuore rimaneva nell'India meridionale.
Cambridge stava diventando una prigione. Ramanujan era abituato alla libertà che offriva la vita in India, dove il clima caldo permetteva alle persone di passare molto tempo all'aria aperta. A Cambridge doveva rifugiarsi dentro le spesse mura del college per proteggersi dal vento gelido e sferzante che proveniva dal Mare del Nord. Le divisioni sociali lo portavano ad avere pochi contatti, al di là delle interazioni formali della vita accademica. Stava anche cominciando a scoprire che l'insistenza di Hardy sul rigore della matematica impediva alla propria mente di vagare libera per Ìl paesaggio matematico.
Al declino del suo stato psicologico si accompagnava un deperimento fisico. Il Trìnity College non comprendeva le rigide regole alimentari che la religione gli imponeva. In India era abituato a ricevere Ìl cibo direttamente nelle mani della moglie mentre luì riempiva i suoi quaderni. Anche se le cucine del college gli offrivano lo stesso servizio riservato ai fellows come Hardy e Littlewood, per Ramanujan il cibo servito alla tavola alta era assolutamente indigesto. Non ce la faceva proprio a sopravvivere senza nessuno accanto e si sentiva terribilmente solo, avendo lasciato sua moglie e fa sua famiglia in India. La malnutrizione produsse una sospetta tubercolosi, che lo costrinse a una serie di ricoveri in diverse case dì cura.
Ramanujan cercò di tirare avanti concentrandosi sulla matematica, ma senza molto successo. I suoi sogni erano pieni di immagini matematiche deliranti. Credeva che Ì suoi dolori addominali fossero causati dalla punta senza fine che si elevava sopra il paesaggio di Riemann dove la funzione zeta andava all'infinito. Era forse una terribile punizione per aver infranto la legge braminìca che gli vietava di attraversare i mari? Aveva frainteso il messaggio di Namagiri? Da quando era arrivato a Cambridge sua moglie non gli aveva più scritto. La pressione da sopportare divenne troppo forte.
Dopo un parziale ristabilimento, ancora depresso, Ramanujan tentò il suicidio gettandosi davanti a un convoglio della metropolitana londinese. Non ci riuscì grazie all'intervento di un guardiano che riuscì a far fermare il treno a pochi metri dal corpo prostrato di Ramanujan. Nel 1917 il tentato suicidio era un reato penale, ma grazie all'intervento di Hardy le accuse contro Ramanujan furono lasciate cadere, a patto che egli si ricoverasse in un sanatorio di Matlock, nel Derbyshìre, dove sarebbe dovuto rimanere sotto controllo medico per dodici mesi.
Alla fine Hardy riuscì a far trasferire Ramanujan in una casa di cura di Putney, un quartiere di Londra. Benché egli confessasse che Ramanujan era stato l'unico vero amore della sua vita, la loro relazione rimaneva pressoché priva di sentimento, se si esclude l'eccitazione di fare matematica insieme. Nel corso di una visita a Ramanujan che giaceva malato, non riuscendo a trovare parole di conforto, Hardy gli citò il numero del taxi con cui era arrivato, 1.729, come esempio di un numero del tutto privo di attrattive. Anche nel suo capezzale, Ramanujan era irrefrenabile: «No, Hardy! No,Hardy! È un numero molto interessante. È il più piccolo numero esprimibile in due modi diversi come somma di due cubi». Aveva ragione: 1.729 = 13 + 123 = 103 + 93.
Le sorti di Ramanujan si risollevarono un po' con la nomina a membro della Royal Society, l'istituzione scientifica più prestigiosa della Gran Bretagna, e alla fine anche con l'elezione afe/low del Trinity College. L'influenza che Hardy esercitò su queste nomine era l'unico modo in cui egli sapeva esprime l'amore di cui parlava. Ma Ramanujan non riacquistò mai la salute. Quando la Prima guerra mondiale finì, Hardy suggerì che forse avrebbe dovuto tornare India per trascorrervi un periodo dì convalescenza. Il 26 aprile 1920; Ramanujan morì a Madras, all'età di trentatré anni, ucciso da una malattia che oggi si ritiene fosse amebiasi, un'infezione dell'intestino crasso che probabilmente aveva contratto prima di partire per l'Inghilterra.
Anche se alla fine Ramanujan non riuscì ad aver ragione dei numeri primi, la sua prima lettera a Hardy ha avuto un effetto duraturo sulla teoria che li riguarda. I matematici si sono convinti che la risposta a questo enigma irrisolto potrà comparire in qualsiasi momento e da qualsiasi fonte. Una nuova intuizione potrebbe proiettare un nome in precedenza sconosciuto dalle ombre di un'esistenza oscura alle luci della ribalta. Come il caso di Ramanujan ha mostrato, talvolta la conoscenza e le aspettative possono frenare i progressi. Gli accademici cresciuti nelle sedi tradizionali della cultura non sono necessariamente nella posizione migliore per uscire dagli schemi. C'è sempre la possibilità che un'altra buchiaia lo ripugnava, tanto che prese l'abitudine di chiedere con insistenza che si girassero tutti gli specchi quando entrava in una stanza. Odiava gli effetti dell'età sulla sua capacità di fare matematica.
La sua Apologià di un matematico è la memorabile descrizione di un matematico alla fine della sua carriera. Per fare matematica, un matematico «non deve essere troppo vecchio. La matematica è un esercizio creativo e non contemplativo, e nessuno ne può trarre gran consolazione quando ha perduto il potere o il desiderio di creare; e questo, a un matematico, è facile che accada molto presto». Come Ramanujan prima dì lui, anche Hardy avrebbe tentato di togliersi la vita, ingerendo pillole invece che saltando davanti a un treno. Ma vomitò le pillole e rimase cieco da un occhio. C.P. Snow ricorda una sua visita a Hardy dopo quel tentativo di suicidio. «Si sbeffeggiava da sé. Aveva combinato un gran pasticcio. C'era mai stato qualcuno che avesse combinato un pastìccio più grande?» La sola consolazione di Hardy, come scrisse nell'Apologià, era Ramanujan. «Ancor oggi, nei momenti di depressione, quando sono costretto ad ascoltare della gente pedante e presuntuosa, mi dico: "Beh, io ho fatto una cosa che voi non sareste mai stati capaci di fare: ho collaborato con Littlewood e Ramanujan quasi su un piano di parità".»
(Tratto da "L'enigma dei numeri primi - Marcus Du Sautoy - 2005 BUR Saggi)
Un racconto su Ramanujan
Un racconto sulla vita del grande matematico indiano Ramanujan
fatto da Marco, 15enne studente liceale.
Srinivasa Ramanujan
