La topologia è una sorta di «ultrageometria», scaturita dalla consueta geometria e dal calcolo infinitesimale, nella quale il matematico studia proprietà molto generali delle superfici e di altri oggetti matematici. Uno dei principali contributi di Poincaré fu quello di escogitare il modo di facilitare tale studio attraverso l'applicazione delle tecniche dell'algebra. La congettura di Poincaré emerse per caso, in seguito a un errore (immediatamente notato) compiuto da Poincaré proprio all'inizio della sua indagine su questa nuova geometria. Gran parte dell'interesse della topologia è concentrata su oggetti matematici a tre o più dimensioni, e l'errore di Poincaré era stato quello di assumere che un fatto alquanto ovvio nel caso di oggetti bidimensionali fosse vero anche per oggetti analoghi tri o n-dimensionali.
Per comprendere questo errore, e per capire il contenuto della congettura di Poincaré, probabilmente la via migliore consiste nel cominciare con una breve discussione della topologia bidirnensionale, per poi passare ad analizzare che cosa comporti il tentativo di passare a un maggior numero di dimensioni.
La topologia bidirnensionale è a volte chiamata, in modo alquanto suggestivo, la «geometria del foglio di gomma ».
La geometria del foglio di gomma
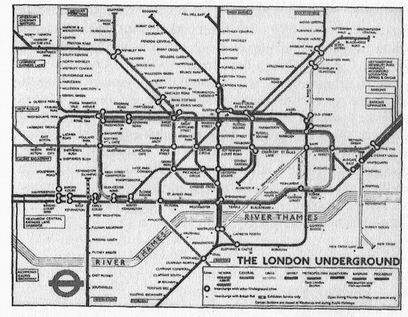
Chiunque abbia visitato Londra - e anche molti di coloro che non ci sono mai stati - riconoscerà la mappa riportata in figura. È la classica mappa della metropolitana di Londra, che troverete affissa dappertutto, non solo nel sistema sotterraneo della città, ma anche riprodotta come motivo ornamentale su vari souvenir: magliette, lazze da caffè e vassoi per la colazione, Progettata nel 1931 da Henry Beck, un disegnatore ventinovenne che lavorava a contratto per il sistema della metropolitana della capitale britannica, è generalmente considerata una delle migliori mappe mai tracciate, e diversi tentativi di migliorarla sono naufragati. In qualche modo, essa riesce a combinare la facilità di consultazione a un aspetto estetico complessivamente piacevole, caratteristiche che ne tanno al tempo stesso un'icona facilmente riconoscibile della Londra contemporanea e un modello per le mappe delle metropolitane di tutto il mondo.
Eppure, quante delle moltissime persone che se ne servono sono davvero consapevoli del modo in cui questa mappa illustra l'immenso potere della topologia? Essa lo fa perché, tranne che in due aspetti, in tutti gli altri è completamente inaccurata. Intanto, non è disegnata in scala, e di conseguenza le distanze sono tutte sbagliate. Inoltre, quelle linee rette così ben tracciate, che rappresentano le traiettorie dei treni, hanno ben poca somiglianzà con le reali linee della metropolitana, dove i passeggeri rischiano di finire a gambe all'aria quando i treni sfrecciano svoltando e curvando sotto le strade di Londra. Il semplice fatto che un tratto di linea sia mostrato nella mappa orientale) da nord a sud, non significa affatto che la lìnea metropolitana che esso rappresenta faccia lo stesso - potrebbe benissimo esser diretta da est a ovest. Una delle due cose che la mappa riporta fedelmente è questa: se una stazione è mostrala a nord del Tamigi, allora nella realtà essa si trova effettivamente a nord del fiume - e lo stesso vale per le stazioni collocate a sud di esso. L'altro aspetto accurato della mappa è il suo modo di raffigurare la rete: l'ordine in cui le stazioni sono collocate su ciascuna linea e i luoghi (le stazioni) in cui due linee si intersecano.
Questa proprietà è davvero l'unica informazione che un utente della metropolitana deve poter leggere sulla mappa: dove salire, dove scendere e dove cambiare linea. La mappa della metropolitana funziona in quanto è assolutamente accurata per quanto riguarda la raffigurazione di quest'unica informazione che i viaggiatori devono conoscere per usare il sistema, sacrificando nel contempo tutti gli altri dettagli a favore di un disegno chiaro e piacevole.
Allo stesso modo lo schema dei circuiti del gruppo di refrigerazione di un supermercato non dice quanto debba esser lungo né dove debba essere collocato ogni tratto di cavo; mostra solo come collegare le diverse componenti - in altre parole, mostra la configurazione della rete. Ancora una volta, lo schema funziona riproducendo in modo accurato l'unica informazione di cui l'ingegnere ha bisogno per mettere a punto il sistema, sacrificando tutti gli altri dettagli alla chiarezza del disegno.
Entrambi questi esempi illustrano l'essenza della topologia bidimensionaie. Se la mappa della metropolitana fosse stampata su un foglio di gomma perfettamente elastico, quest'ultimo potrebbe essere stirato e compresso in modo da rendere corretto ogni dettaglio, ottenendo così una classica mappa geograficamente accurata, disegnata in scala, con ogni tratto dì linea correttamente orientato rispetto ai punti cardinali. Questa operazione non influenzerebbe le modalità di connessione delle varie stazioni da parte delle linee. In termini matematici, ciò si spiega tenendo presente che la configurazione di una rete (definita come un insieme di punti connessi da varie lìnee) è una proprietà topologica. In parole povere, le reti sono oggetti topologici. Potete torcere o stirare una qualsiasi delle linee di una rete senza modificarne la configurazione complessiva. Per alterare la rete, occorre spezzare una connessione o aggiungerne una nuova.
Quello che vale per la metropolitana di Londra, vale per qualsiasi rete. Vale per gli schemi dei circuiti elettrici e per gli stessi circuiti, per i chip dei computer, per le reti telefoniche e per Internet. Ecco perché la geometria del foglio di gomma è una delle più importanti branche della matematica oggi esistenti. Nel caso della mappa della metropolitana, fintanto che essa è topologicamente accurata, l'esattezza del disegno non ha importanza.
In generale, la topologia bidimensionale (la geometria del foglio di gomma) studia le proprietà di figure le quali, se disegnate su un (ipotetico) foglio di gomma perfettamente elastico, si conservano quando esso viene deformato e stirato. Come vedremo, le configurazioni delle reti non sono che una delle diverse proprietà non influenzate da tali manipolazioni. In effetti, sebbene le mappe siano sempre state importanti, e per quanto fondamentale sia Ea matematica delle reti nel mondo contemporaneo, non furono queste le applicazioni che motivarono, in origine, lo studio della topologia. In realtà, lo sviluppo dì questa materia non fu sollecitato da esigenze nate in un'area della matematica applicata. Piuttosto, la topologia emerse dal cuore stesso della matematica pura, in particolare dagli sforzi tesi a comprendere come mai il calcolo differenziale funzionasse.
Verso la fine del diciannovesimo secolo, i matematici cominciarono a studiare con grande attenzione gli assunti, a volte espliciti, ma più spesso impliciti, alla base della loro materia. In larga misura, erano motivati dal desiderio di capire come funzionasse il calcolo infinitesimale, Dal momento in cui Newton e Leibniz lo avevano introdotto, a metà del diciassettesimo secolo, i matematici se ne erano serviti a piene mani e con successo: il calcolo, insomma, funzionava. Ciò nonostante, nessuno aveva capito chiaramente perché. Era come una sorta di magia.
La spiegazione matematica del funzionamento del calcolo infinitesimale fu raggiunta grazie agli sforzi cumulativi di moltissimi matematici, nell'arco di un periodo di tre secoli. Per arrivare a una spiegazione, essi dovettero eseguire un'analisi dettagliata della natura dei numeri reali, dei processi infiniti (come le somme e i prodotti nei quali ci siamo imbattuti nel capitolo 1), e dello stesso ragionamento matematico.
L'impulso verso un'analisi ancor più dettagliata fu accompagnato - e in larga misura motivato - da un impressionante aumento di astrazione. Come abbiamo visto nel capitolo 1, a metà del diciannovesimo secolo, la matematica andò incontro a una sorta di rivoluzione e da quel momento, è andata facendosi sempre più astratta. Per la maggior parte della sua storia, la matematica si è occupata di oggetti e modelli emergenti dall'esperienza quotidiana. L'aritmetica ha a che fare con i numeri, che - sebbene tecnicamente astratti - sono parte integrante del tessuto della nostra vita. Anche i numeri reali, con tutte le loro difficoltà, derivano dall'idea semplice e intuitiva di una retta continua. La geometria ha a che fare con versioni idealizzate delle forme che vediamo quotidianamente intorno a noi. La teoria delle probabilità esamina eventi casuali, familiari a chiunque abbia lanciato una moneta o giocato a carte o a dadi. E per quanto i simboli e le equazioni dell'algebra possano sembrare astratti ai non matematici, prima dell'ultimo scorcio del diciottesimo secolo generalmente quei simboli denotavano numeri, e pertanto la loro aria astratta era essenzialmente un'illusione linguistica.
Il diciannovesimo secolo, d'altro canto, vide la comparsa di una gran quantità di oggetti e modelli nuovi che decisamente non facevano parte dell'esperienza quotidiana - o, per essere più precisi, che non erano riconosciuti coinè tali (poiché la maggior parte di essi proveniva da un'attenta analisi della matematica esìstente, presumibilmente facevano parte della vita quotidiana, una parte nascosta, però - una sorta di scheletro). Fra i nuovi oggetti e modelli studiati dai matematici negli ultimi centocinquant'annì troviamo geometrie in cui le linee parallele si incontrano (denominate « geometrie non euclidee»), geometrie a quattro e più dimensioni, geometrie a dimensione infinita, un'algebra in cui i simboli indicano simmetrie delle figure (denominata « teoria dei gruppi »), un'algebra in cui i simboli indicano pensieri logici (la «logica proposizionale») e un'algebra in cui i simboli indicano il moto in uno spazio bi- o tri-dimensionale (« algebra vettoriale »).
Lo sviluppo della topologia ebbe luogo nel contesto di questa proliferazione di nuove astrazioni. L'idea era quella di sviluppare una « geometria » che studiasse le proprietà di figure che non vengono distrutte da una deformazione continua e che pertanto non dipendono da concetti quali linee rette, cerchi, cubi, e così via, né dalla misura di lunghezze, aree, volumi o angoli. Gli oggetti studiati in topologia erano denominati « spazi topologici » (proprio come la geometria può essere definita lo « studio degli spazi geometrici » - per esempio quello euclideo bidimensionale, familiare a tutti per averlo studiato nella geometria delle scuole superiori).
Il nesso fra la topologia e lo sforzo teso a comprendere il funzionamento del calcolo infinitesimale è alquanto sottile. Essenzialmente, entrambi dipendono dalla capacità di manipolare l'infinitamente piccolo. Nel capitolo 4 abbiamo visto il perché di ciò nel caso rlcl raliolo, Ma nis'liamio ila spari ire le trasformazioni inpolojiji'lie cuii l'iiilìuitaiiieiiie piccolo? La risposta è: nulo. In ell'elii, esse forniscono una chiave per affrontare davvero I1 infinitamente piccolo. II punto è questo: iiunitivamente, l'essenza di una trasformazione topologica sta nel fatto che due punti « infinitamente vicini » prima di essa rimangono «infinitamente vicini» anche dopo (fra un momento vi spiegherò il perché di quelle virgolette nell'ultima frase). In particolare, né lo stiramento, né la compressione, e nemmeno la torsione di un foglio di gomma distruggerà la prossimità di due punti inizialmente vicini, che rimarranno tali anche una volta completata la manipolazione.
A questo punto dovete stare un poco attenti. Il concetto qui implicato è quello di vicinanza relativa a tutti gli altri punti dello spazio topologico. Noi possiamo stirare il foglio in modo che due punti inizialmente vicini non ci sembrino più tali. In questo caso, però, l'alterazione in termini di «vicinanza» è un cambiamento geometrico imposto dall'esterno. Dalla prospettiva del foglio di gomma, i due punti rimangono vicini. II solo modo per distruggere quella vicinanza consiste nel tagliare o lacerare il foglio - un'operazione che in topologia è proibita.
Affinchè la topologìa potesse spiccare il volo, i matematici dovettero trovare un modo per comprendere a fondo il concetto essenziale di «vicinanza relativa». Si accinsero a farlo cercando un modo di cogliere l'ipotetico concetto di due punti «infinitamente vicini». È intuitivo che una trasformazione topologica ha la seguente proprietà: se due punti sono infinitamente vicini in origine, tali rimarranno dopo la trasformazione. Con questo approccio, il problema stava nella vaga definizione del concetto di « infinitamente vicino ».3 D'altra parte, accostandosi in questo modo alle trasformazioni topologiche, i matematici riuscirono a trovare il modo di definire con precisione una trasformazione topologica (spiegare adesso di quale definizione si tratti comporterebbe una digressione troppo lunga). A quel punto, essi si trovarono, per così dire, in condizioni di poter capovolgere l'analisi, e si servirono del concetto di «trasformazione topologica » (ora definito in modo appropriato e ben compreso) per procedere a un'analisi precisa del concetto intuitivo di «infinitamente vicino», dal quale erano partiti. Così facendo, riuscirono a sviluppare il calcolo infinitesimale in modo rigoroso, evitando il concetto problematico di « infinitamente vicino » e usando invece come base portante la topologia.
Questa è la principale ragione per cui Poincaré e altri si dedicarono allo sviluppo della topologia.
Un dubbio ovvio che viene in mente a chiunque si imbatta per la prima volta nella topologia è se si possa dire qualcosa di interessante sugli spazi topologici. Dopo tutto, una volta che si cominciano a escludere qualità importanti come la linearità delle rette o la piattezza dei piani, non c'è alcuna garanzia di ritrovarsi, alla fine del processo, con qualcosa di valore fra le mani. Gli spazi topologici non solo non contengono linee rette, ma mancano anche completamente del concetto di « forma fissa », né esiste in essi alcun tipo di distanza. L'unica cosa che sì può stabilire è quando due punti siano o no reciprocamente vicini. Questo può andare benissimo per offrire solide basi al calcolo infinitesimale, ma se restiamo nell'ambito della topologia, dove ci può portare?
L'esempio della metropolitana di Londra dimostra che la topologia non è una materia del tutto priva di ricadute. Anzi, sorprendentemente essa si è rivelata una delle branche più profonde e affascinanti della matematica contemporanea, con molteplici applicazioni nella stessa matematica, in fisica e in altri campi. Per menzionare solo una delle sue importanti applicazioni, basti pensare che la topologia rappresenta la base matematica della teoria delle superstringhe, la più recente formulata dai fisici sulla natura dell'universo.
Diamo dunque un'occhiata ad alcuni degli oggetti studiati dai topologi. Per semplicità, mi atterrò al caso bidimensionale (la geometria del foglio di gomma) e mi chiederò quali proprietà della comune geometria delle superiori portare nella topologia. Poiché lo stiramento e la torsione del foglio di gomma modificheranno le rette in curve e altereranno distanze e angoli, in topologia nessuno di questi familiari concetti geometrici ha alcun significato. Ma allora, che cosa rimane?
Restano ancora le linee, purché non si pretenda che siano rette o circolari, né che abbiano una forma particolare. E che altro? Che dire delle linee chiuse, le linee che si chiudono su se stesse? Se disegnate un anello su un foglio di gomma perfettamente clastico, non importa quanto lo stiriate, lo comprimiate o lo torciate, l'anello rimarrà un anello. Che altro ancora?
Per rispondere, dimostrerò il primissimo teorema matematico che possa essere legittimamente denominato «topologico». Lo dobbiamo al grande matematico svizzero Eulero. Nel 1735, egli risolse un annoso enigma, il cosiddetto « problema dei ponti di Kònigsberg».
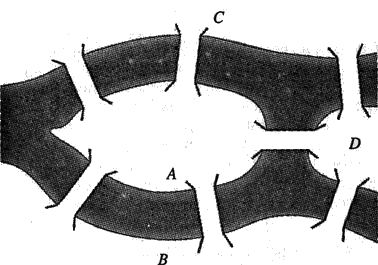La città di Kònigsberg, che sorgeva sul fiume Pregel, nella parte orientale della Prussia (oggi si chiama Kaliningrad, ed è in Russia) aveva due isole, fra loro unite da un ponte. Un'isola era connessa a ciascuna riva da un solo ponte, mentre l'altra isola aveva due ponti su ciascuna riva.
Ogni domenica, molti cittadini di Kònigsberg erano soliti fare una passeggiata con la famiglia; abbastanza naturalmente, il loro itinerario li portava spesso a percorrere i diversi ponti della città. Spesso essi si chiedevano se esistesse un itinerario tale da attraversare cia-scun ponte una e una sola volta.
Eulero, resosi conto che l'esatta topografia dell'isola e dei ponti era irrilevante, risolse il problema. Quel che davvero contava era il modo in cui i ponti erano connessi: in altre parole, la rete che essi formavano. II problema, insomma, era un problema topologico, e non geometrico. Esso non si modifica se disegniamo la rete di pontì-e-isole in modo più schematico, come mostra la figura 5.4. Nel disegno semplificato si vede che ci sono esattamente quattro punti (di solito chiamati «nodi» o « vertici » della rete) connessi da sette linee (denominate « lati » o « spigoli » della rete).
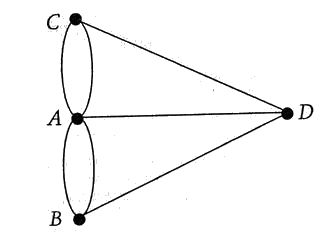Giunto a questo punto, Eulero ragionò come segue. Prendiamo una rete qualsiasi e immaginiamo un itinerario che percorra ciascun Iato esattamente una sola volta. Ogni nodo che non sia il punto di partenza o il punto d'arrivo dell'itinerario deve rappresentare il punto d'incontro di un numero pari di spigoli, che possano così essere appaiati in coppie ingresso-uscita. Nella rete dei ponti, però, tutti e quattro i vertici hanno un numero dispari di spigoli che vi si incontrano. Pertanto un tale itinerario non può esistere. Di conseguenza, non esiste un tragitto che porti a percorrere i ponti di Kònigsberg una e una sola volta ciascuno.
La soluzione del problema dei ponti di Kónigsberg fu il primo teorema topologico di Eulero - in effetti il primo teorema topologico del mondo - ma non fu certo l'ultimo o il più significativo affrontato dal matematico svizzero. Quel riconoscimento va quasi sicuramente a uno straordinario risultato topologico da lui scoperto a proposito delle reti. Eulero dimostrò che per qualsiasi rete tracciata su una superfìcie piatta, se V è il numero totale dei vertici (o nodi), se £ è il numero totale degli spigoli (o linee di connessione), e se F è il numero totale delle « facce » (ossia delle regioni racchiuse da tre o più spigoli), allora vale la seguente semplice formula:
V - E + F = 1
La rete tracciata da Eulero per rappresentare il problema dei ponti di Kónigsberg, per esempio, ha V = 4, E = 7 ed F = 4, e quindi
V - E + F = 4 - 7 + 4 = 1
Per fare un altro esempio, basta osservare la semplice rete riportata qui a fianco. In questo caso, V = 7, E = 10, F = 4, perciò
V - E + F = 7 - 10 + 4 = 1
Il fatto davvero degno di nota è che l'espressione V - E + F è uguale a 1 per tutte le reti mai tracciate, e per tutte quelle che saranno tracciate in futuro. Eulero ne diede una dimostrazione molto semplice. L'idea generale consiste nel partire con una rete qualsiasi e poi, uno per uno, nell'eliminare gli spigoli e i nodi terminali (nodi sui quali arriva solo uno spigolo). La rimozione di uno spigolo che non sia diretto a un nodo terminale porta a una diminuzione di una unità sia E che F, mentre lascia immodificato V; il valore di V — E + F pertanto non cambia. Se si rimuove un nodo terminale, si rimuove anche lo spigolo che porta a esso: tale operazione non modifica F, ma diminuisce di una unità sia V che E - e quindi, ancora una volta, V — E + F non cambia. Questo processo terminerà quando sarete rimasti con un unico nodo. Per questa rete banale, V=1, E=0 ed F=0,cosìche V - E + F = 1. D'altra parte, il valore di V — E + F rimaneva lo stesso durante tutto il processo di riduzione. Pertanto, il valore originale di V — E + F della rete di partenza doveva essere pari a 1. Sebbene Eulero abbia, rispettivamente, risolto uno dei primi enigmi e dimostrato uno dei primi teoremi della topologia, in realtà questa disciplina prese l'abbrivio solo alla fine del diciannovesimo secolo, quando entrò in scena Poincaré.
Ecco dunque la storia fino a oggi. In topologia noi studiamo le proprietà di figure e oggetti che rimangono immodificati in seguito a una deformazione continua. Per « continua » intendiamo che essa non comporti operazioni di taglio, strappo o saldatura (spesso i matematici escludono anche la creazione o la distruzione di qualsiasi piegatura o punta acuta).
Vorrei dunque ribadire che il semplice fatto di non riuscire a trovare una trasformazione continua che converta un oggetto in un altro non costituisce una prova definitiva della diversità topologica dei due oggetti. Quel che occorre è trovare una qualche proprietà topologica - per esempio una proprietà che non cambi in seguito a deformazione continua - posseduta da uno dei due oggetti ma non dall'altro.
Abbiamo già incontrato una di tali proprietà. Come abbiamo visto prima, per qualsiasi rete, il valore della quantità V - E + F è una proprietà topologica: la quantità è la stessa per tutte le reti. Inoltre, una deformazione continua della superficie su cui è disegnata la rete non altera le connessioni della rete stessa e pertanto non modifica nessuno dei valori V, E e F. Nel caso che abbiamo considerato - in particolare, le reti disegnate su un piano - il valore di V — E + F dà 1 (e poiché questo è il valore calcolato su un piano, ne consegue che è il valore per una rete disegnata su qualsiasi foglio, non importa quanto esso sia contorto e incurvato). Se consideriamo reti disegnate sulla superficie di una sfera, ossia che ricoprano l'intera sfera, e non solo una parte di essa, allora V — E + F — 2. Per reti tracciate su un toro (anche in questo caso disegnate in modo da coprirlo interamente), allora V — E + F — 0. Pertanto, possiamo concludere con assoluta tranquillità che un piano bidimensionale, una superficie sferica e la superfide di un toro sono tutte entità topologicamente diverse. Per reti tracciate su un doppio toro (la forma del numero S),V -E + F = —2 e quindi ora sappiamo anche che un doppio toro è diverso da un piano, da una sfera e da un toro.
Nel caso dì queste quattro particolari superfici, naturalmente, è davvero evidente che nessuna di esse può essere trasformata in nessuna delle altre mediante una deformazione continua. Come mostra il nostro puzzle degli anelli alla figura 5.7, però, quando ci si allontana un poco da sfere e tori, le cose diventano di gran lunga meno ovvie.
Il valore dell'espressione V - E + F per qualsiasi rete tracciata su una particolare superficie è un esempio di quello che i matematici chiamano « invariante topologica della superficie ». Ciò significa che questo valore rimane invariante se sottoponiamo la superficie a una trasformazione topologica {ossia a una deformazione continua). Il valore di V — E + F è denominato « caratteristica di Eulero della superficie», in onore di colui che per primo dimostrò come tale quantità sia la stessa per ogni rete disegnata su un piano piatto. Essa è una delle invarianti topologiche note che possono essere usate per determinare se due particolari superfici siano topologicamente equivalenti oppure no.
Un'altra invariante topologica è il numero cromatico di una superficie, un concetto che ha le sue origini in un classico problema riguardante la colorazione delle mappe. Nel 1852, un giovane matematico inglese, Francis Guthrie, sì pose questa domanda apparentemente innocua: qual è il numero minimo di colori che occorrono per colorare le diverse regioni di una qualsiasi mappa? L'unica condizione è che due regioni qualsiasi, le quali condividano un tratto di confine, siano colorate in modo diverso (se due regioni si toccano in un singolo punto, d'altra parte, si considerano come non aventi un confine comune). Tracciare mappe che richiedano quattro diversi colori è semplicissimo, ma esistono mappe che ne richiedano cinque? La risposta è no, ma per dimostrarlo occorse più di un secolo - e quando finalmente la dimostrazione fu prodotta, nel 1976, il suo ottenimento non comportò solo l'uso di sofisticati ragionamenti matematici, ma anche un significativo ricorso al computer. In effetti, il « teorema dei quattro colori », come poi esso divenne famoso, fu il primo fondamentale risultato matematico in cui l'impiego di un computer fu considerato inevitabile.
Poiché la deformazione continua del foglio su cui è tracciata una mappa non altererà l'eventuale condivisione dei confini, il teorema dei quattro colori è chiaramente un risultato topologico. Due regioni che condividano un tratto di confine prima della deformazione, continueranno a condividerlo anche dopo - e viceversa. Pertanto, una colorazione della mappa che sia corretta prima della deformazione sarà ancora tale dopo di essa.
II teorema dei quattro colori, proprio come la domanda originaria alla quale risponde, riguarda mappe tracciate su un piano. D'altra parte, possiamo benissimo porci la stessa domanda relativamente a mappe tracciate su superfici qualsiasi. Il numero cromatico di una superficie è il numero minimo di colori necessari per colorare una mappa qualsiasi tracciata su quella superficie. In base al teorema dei quattro colori, il numero cromatico di un piano è 4. Uguale è il numero cromatico della superficie di una sfera (ta dimostrazione del teorema dei quattro colorì funziona per mappe tracciate su un piano o su una sfera). Quanto a un toro, il suo numero cromatico è 7.
Facce e superfici
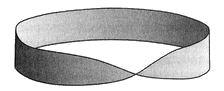Un'altra invariante topologica ha le sue origini nel concetto di «numero di facce « - in altre parole dipende dal fati» che una superficie abbia una o due facce. Di primo acchito, la cosa sembra stupida. Certo: qualsiasi superficie ha due facce, no? No, la risposta è no. È facile costruire una superficie con una faccia sola. Prendete una lunga striscia di carta, per esempio larga 3 centimetri e lunga 30, fatele fare una mezza torsione, e poi incollate i due estremi in modo da formare una striscia una superficie con una faccia sola. Potete controllare: prendete una matita e tracciate una linea lungo la striscia, nel mezzo. Scoprirete che la linea percorre la striscia due volte per poi tornare al punto di partenza. Poiché una linea non può passare da un lato all'altro di una superficie senza attraversare i bordi della superficie stessa, questo dimostra che la striscia in questione ha una faccia sola. Essa è nota come «nastro di Mòbius», e prende il nome dal matematico tedesco che la scoprì.
Oltre ad avere una sola faccia, il nastro di Móbius ha anche solo un bordo. Lo si può verificare colorando il bordo della striscia con una marita. Se colorate uno dei bordi di una striscia normale, per esempio cilindrica, l'altro rimarrà non colorato. Se invece provate con un nastro di Mòbius, scoprirete che alla fine non c'è un bordo rimasto senza colore. L'intero bordo, che è unico, sarà tutto colorato.
Come suggerisce l'esempio del nastro di Mòbius, il numero di facce della superficie è legato all'esistenza dei bordi. In massima parte, i matematici si concentrano su supeiiìci prive di bordi, quelle che chiamano « superfìci chiuse ». Inoltre, le proprietà topologiche più interessanti hanno a che fare con la struttura interna della superficie, con il suo modo di torcersi e curvarsi. In effetti, per ogni superfìcie che abbia uno o più bordi, esiste in genere una superficie chiusa che ha più o meno le stesse caratteristiche. Per esempio, una sfera ha caratteristiche simili a quelle di un piano finito {come un disco piatto), e quando dimostriamo un risultato topologico per una sfera, generalmente esso ha immediate conseguenze anche per un piano piatto, e viceversa (intuitivamente questo avviene perché possiamo prendere un foglio piatto perfettamente estensibile e unire i suoi bordi formando un sacchetto chiuso: topologicamente una sfera).
La superficie chiusa corrispondente al nastro di Mòbius è denominata « bottiglia di Klein », in onore del suo scopritore, Felìx Klein. La bottiglia di Klein non ha bocca, e non ha nemmeno un interno o un esterno (oppure, se vogliamo esprimere la stessa cosa con parole diverse, l'interno e l'esterno sono indistinguibili). In teoria, è possibile costruire una bottiglia di Klein prendendo due strisce di Mòbius e incollandole lungo il loro unico margine. Dico in teoria, perché nel consueto spazio tridimensionale è impossibile eseguire l'operazione di saldatura. La bottiglia di Klein esiste (come oggetto matematico) solo nello spazio quadridimensionale. Nel nostro mondo tridimensionale, la cosa migliore che si possa fare è permettere che la superficie passi attraverso se stessa.
Molti matematici, tengono nel loro studio, come soprammobile, una bottiglia di Klein di vetro, autointersecante. In quattro dimensioni, la bottiglia non dovrebbe passare attraverso se stessa. Per l'uomo della strada, un oggetto che esiste solo nello spazio
quadridimensionale non esiste davvero, naturalmente; d'altra parte, questa obiezione banale non agisce da deterrente sui matematici. In fondo, tutti «sanno» che i numeri negativi non hanno radici quadrate, ma questo non ha impedito ai matematici di sviluppare i numeri complessi né di servirsene in applicazioni pratiche. Gran parte dell'immenso potere della matematica scaturisce proprio dal fatto che è possibile usarla per studiare oggetti al di là della nostra ordinaria concezione di creature che vivono in uno spazio a tre dimensioni.
Per esempio, possiamo studiare le proprietà di reti disegnate su una bottiglia di Klein. Quando lo facciamo, scopriamo che la caratteristica di Eulero di una bottiglia di Klein (ossia il valore dell'espressione V - E + F) è O, lo stesso che per il toro. Ahhh! Questo significa forse che la bottiglia di Klein è topologicamente equivalente al toro? No: sebbene la caratteristica di Eulero non possa distinguere una bottiglia di Klein da un toro, il numero cromatico può farlo. Il numero cromatico di uria bottiglia dì Klein è 6, mentre quello del toro è 7.
La proprietà topologica di una bottiglia di Klein corrispondente alla natura mono-faccia della sua superfìcie è uno strano concetto, che prende il nome di « non orientabilità». In altre parole, sulla superficie di una bottiglia di Klein non è possibile distinguere orientamenti destrorsi o sinistrorsi, né una rotazione oraria o antioraria. Se disegnaste una piccola mano sinistra sulla superficie di una bottiglia di Klein, e poi faceste scivolare il disegno su di essa portandolo abbastanza lontano dal punto d'origine (abbastanza lontano perché - se la bottiglia di Klein fosse nello spazio tridimensionale - la mano passi attraverso il collo autointersecante), quando essa tornerà al punto di partenza scoprireste che si è prodigiosamente trasformata in una piccola mano destra.
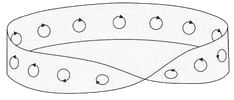Questo esperimento è più facile da eseguire con un nastro di Mòbius. Disegnate una piccola mano sinistra sulla superficie della striscia, e poi tracciatene diverse copie adiacenti fino a tornare al punto di partenza, dove scoprirete che la mano sinistra è diventata una mano destra. Altrimenti, potete disegnare un piccolo cerchio con una freccia che indichi una rotazione in senso orario sulla superficie di una bottiglia di Klein o di un nastro di Mòbius; fate poi scivolare la figura {o copiatela) su tutta la superficie, fino a tornare al punto di partenza: scoprirete che la vostra freccia ora punta in senso antiorario .
Una superficie sulla quale non sia possibile trasformare la mano destra nella sinistra o il senso orario in quello antiorario semplicemente facendo scivolare su di essa delle figure, è detta « orierttabile ». Una sfera o un piano, per esempio, sono orientabili, e altrettanto sono un toro e un doppio toro. Una superficie, come quella della bottiglia di Klein (o di un nastro di Mòbius), dove tali cambiamenti sono possibili, è detta invece « non orientabile ». L'orientabilità (o la non orientabiiità) è un'invariante topologica.
Uno dei primi successi della topologia fu quello di dimostrare che due sole invarianti topologiche, precisamente la caratteristica di Eulero e l'orientabilità, bastano per riuscire a distinguere due superfici chiuse qualsiasi. Ciò significa che se due superfici hanno la stessa caratteristica di Eulero e sono entrambe orientabili (o non orientabili) allora sono di fatto la stessa cosa - e questo anche se voi, per quanti sforzi facciate, non riuscite a capire come trasformare l'una nell'altra con una deformazione contìnua. Questo risultato è stato denominato «teorema della classificazione delle superfici», poiché afferma la possibilità (da un punto di vista topologico) di classificare tutte le superfici avvalendosi di questi due soli attributi.
In termini approssimativi, possiamo dimostrare il teorema della classificazione delle superfici prendendo una sfera come superficie fondamentale e misurando il grado in cui qualsiasi altra superficie data differisca da essa - ovvero, verificando che cosa si debba fare alla sfera per trasformarla in quella superficie. Questo corrisponde alla nostra comune intuizione, che vede nella sfera la superfìcie chiusa più semplice, più fondamentale e, come potrebbe dire qualcuno, esteticamente più perfetta.
Nei primi anni del ventesimo secolo, Poincaré e altri matematici si accinsero a classificare gli analoghi delle superfici a più dimensioni - che chiamarono « varietà ». Essi tentarono, il che non sorprende, un approccio simile a quello che aveva funzionato con le superfici a due dimensioni. Cercarono cioè di classificare tutte le varietà tridimensionali (denominate sinteticamente « 3-varietà») prendendo come elemento fondamentale un analogo tridimensionale della sfera (denominata « 3-sfera») e misurando il grado in cui ogni varietà tridimensionale differisce dalla 3-sfera.
Qui occorre fare attenzione. Una superficie regolare come una sfera o un toro è un oggetto bidimensionale. La figura racchiusa dalla superficie, naturalmente, è tridimensionale, ma la superficie, di per se stessa, è bi-dimerisionale. A parte il piano, qualsiasi superficie può essere costruita solo in uno spazio a tre o più dimensioni. Pertanto, qualsiasi superfìcie chiusa richiede tre o più dimensioni. Per esempio, occorrono tre dimensioni per costruire una sfera o un toro, quattro per costruire una bottiglia di Klein. Ciò nonostante una sfera, un toro o una bottiglia di Klein sono oggetti bidimensionali, una superficie priva di spessore che può, in linea di principio, essere costruita con un foglio piatto, perfettamente elastico.
Ma allo stesso modo in cui una sfera può essere considerata un analogo bidimensionale (nello spazio tridimensionale) dì un cerchio (che è un oggetto monodimensionale - una linea curva - nello spazio bidimensionale), possiamo immaginare l'analogo tridimensionale (nello spazio quadridimensionale) di una sfera. Be', in realtà non possiamo immaginarlo. Possiamo però scrivere le equazioni che determinano tale oggetto e « studiarlo» dal punto di vista matematico. In effetti, i fisici studiano comunemente questi oggetti immaginar!, e si servono dei risultati per aiutarsi a comprendere l'universo in cui viviamo. Le varietà tridimensionali, ossia gli analoghi tridimensionali delle superfici (che esistono in spazi quadri- o n-dirnensionali) sono a volte denominate «ipersuperfici», e l'analogo tridimensionale di uria sfera è denominato «ipersfera».
Non esiste alcuna ragione matematica che imponga di fermarsi a tre dimensioni. Potete scrivere equazioni che determinano varietà di tre, quattro, cinque, sei o qualsia-si altro numero di dimensioni. Ancora una volta, queste considerazioni rivelano di essere qualcosa di più di speculazioni oziose. Secondo le teorie matematiche della materia su cui i fisici stanno attualmente lavorando, l'universo nel quale viviamo avrebbe undici dimensioni. Stando a queste teorie, noi siamo direttamente consapevoli di tre di esse, mentre le altre si manifestano sotto forma di vari aspetti fisici, per esempio la radiazione elettromagnetica e le forze che tengono insieme gli atomi.
Poincaré tentò di classificare le varietà tri o n-dimensionali prendendo come figura fondamentale una « sfera» di dimensioni corrispondenti, e poi applicandole processi di chirurgia topologica. Un primo passo naturale in questo sforzo fu quello di cercare una semplice proprietà topologica che indicasse quando una data superficie (bidimensionale) è topologicamente equivalente a una sfera. (Ricordate, qui stiamo facendo della topologia: anche nel caso più semplice delle superfici bidimensionali, una superficie potrebbe apparire estremamente complicata e ciò nondimeno rivelarsi deformabile in modo continuo fino a dare una sfera.)
Nel caso delle superfici bidimensionali, una tal proprietà esiste. Supponiamo di disegnare con una matita un semplice cappio chiuso sulla superficie di una sfera. Ora, immaginiamo di far contrarre le dimensioni del cappio, il quale, nel contrarsi, scivolerà sulla superficie. Esiste un limite alla sua contrazione? Ovviamente no. Possiamo farlo restrìngere finché sarà indistinguibile da un punto. In senso matematico la sua contrazione potrà procedere davvero finché esso si sarà ridotto a un punto.
La stessa cosa non è necessariamente vera se si esegue l'esperimento disegnando un cappio intorno a un toro. È possibile infatti disegnare cappi intorno a un toro in modo che essi non possano contrarsi fino a ridursi a un punto. In particolare, non sarà possibile far contrarre indefinitamente un cappio disegnato attorno all'anello del toro, né un cappio che circondi il toro come una cintura.
La contraibilità di qualsiasi cappio venga disegnato su una sfera, fino alla sua riduzione a un punto, è una proprietà topologica superficiale esclusiva delle sfere. In altre parole, se avete una superfìcie sulla quale qualsiasi cappio (qui è molto importante quel «qualsiasi») possa esser fatto contrarre fino a ridursi a un punto senza mai staccarsi dalla superficie, allora quella superficie è topologicamente equivalente a una sfera.
Lo stesso vale anche per un'ipersfera tridimensionale? Ecco la domanda che Poincaré si pose al principio del secolo scorso, nella speranza che una rapida risposta positiva rappresentasse il primo passo lungo la strada che l'avrebbe portato a un teorema per la classificazione di ipersuperfici tridimensionali. Poincaré sviluppò un metodo sistematico - denominato « teoria dell'omotopia» - per studiare (avvalendosi dei metodi dell'algebra) che cosa succede ai cappi che vengono spostati e deformati su una varietà.
In effetti, le cose non andarono proprio così. All'inizio, Poincaré assunse tacitamente che la proprietà della contrazione del cappio per varietà tridimensionali caratterizzasse davvero la 3-sfera. Dopo un po', però, si rese conto che il suo assunto avrebbe potuto non esser corretto, e nel 1904 pubblicò i suoi dubbi, scrivendo (in francese): «Si consideri una varietà tridimensionale compatta V senza bordi. È possibile che il gruppo fondamentale di V possa essere banale, anche se V non è omeomorfo alla sfera tridimensionale? » Eliminando la terminologia tecnica, quel che Poincaré si stava chiedendo era: « È possìbile che una varietà tridimensionale presenti la proprietà di consentire la contrazione di un cappio senza essere equivalente a una 3-sfera? » Ecco come nacque la congettura di Poincaré.
La sua domanda, emerse poi, non era destinata a ottenere una risposta veloce - e nemmeno, se è per questo, una risposta lenta, nonostante numerosi insigni topologi le abbiano dedicato tutti i propri sforzi. Di conseguenza, dimostrare (o anche confutare) la congettura di Poincaré finì per diventare uno dei traguardi più ambiti della matematica.
Un progresso, di qualsiasi natura, impiegò molto tempo a realizzarsi. Nel 1960, il matematico americano Ste-phen Smale dimostrò che la congettura di Poincaré era vera per varietà di qualsiasi dimensione da cinque in su. Pertanto, se ima varietà penta- o Tirdimcnsionale ha la proprietà che qualsiasi cappio chiuso disegnato su di essa può essere fatto contrarre fino a ridursi a un punto, allora quella varietà è topologicamente equivalente a un'ipersfera di dimensioni corrispondenti.
Purtroppo, Smale usò metodi che non funzionavano per varietà tri o quadri-dimensionali, e quindi la congettura originale rimase irrisolta. Poi, nel 1981, un altro americano, Michael Freednian, trovò il modo di dimostrare la congettura per varietà quadridimensionali (il lavoro di Freedman si rivelò poi utilissimo per i fisici che studiano la natura della materia).
Questo è lo status in cui oggi versa il problema. La congettura di Poincaré è stata dimostrata per tutte le dimensioni eccetto tre: proprio quella per la quale Poincaré aveva in origine sollevato la questione. Per i loro contributi, sia Smale che Freedman furono insigniti di una medaglia Fields, in genere considerata l'equivalente di un premio Nobel per i matematici. Senza dubbio un onore simile sarebbe tributato anche alla prima persona che dimostrasse l'ultimo caso rimanente della congettura di Poincaré. (Purché quell'individuo abbia meno di quarantenni, l'età limite per ricevere la medaglia Fields. Le medaglie infatti furono istituite per incoraggiare i giovani matematici a risolvere i fondamentali problemi della disciplina.)
L'aspirante risolutore dovrebbe forse cercare una dimostrazione della congettura, oppure cercare un controesempio - ovvero un'ipersuperficie tridimensionale che pur permettendo la contrazione di un cappio non avesse la proprietà di essere topologicamente equivalente a una ipersfera tridimensionale? Giacché la congettura di Poincaré è stata già dimostrata per tutte le altre dimensioni, prevedibilmente le scommesse più intelligenti sono quelle che puntano sulla sua conferma. D'altra parte potrebbe benissimo darsi che ia dimostrazione sia lunga centinaia di pagine. L'ultima volta che qualcuno produsse una presunta dimostrazione, che divenne oggetto di seria considerazione da parte della comunità dei matematici - evento che risale a circa vent'anni fa -occorsero diversi mesi per esaminarla attentamente prima di raggiungere un unanime consenso sul fatto che conteneva un errore fatale.
(Tratto da "I problemi del millennio - Keith Devlin- 2002 Longanesi & C.)
Henri Poincaré
