Armonia musicale

Nel mondo dei pitagorici l'ordine numerico era lungi dal riguardare solo i triangoli e la geometria. La tradizione attribuisce a Pitagora la scoperta della progressione armonica delle note della scala musicale, attraverso la constatazione che gli intervalli musicali e l'altezza delle note corrispondono alla lunghezza relativa delle corde in vibrazione. Pitagora osservò che dividere una corda tesa in base a numeri interi consecutivi permetteva di generare (entro certi limiti) suoni armoniosi e piacevoli, o «consonanti». Se due note (due vibrazioni regolari) scelte a caso sono prodotte contemporaneamente, il suono che ne risulta è per lo più sgradevole (o «dissonante»). Solo poche combinazioni sono gradevoli. Pitagora scoprì che queste rare consonanze si ottengono quando le note prodotte da corde dello stesso tipo poste in vibrazione hanno lunghezze i cui rapporti corrispondono a quelli dei primi numeri interi. L'unisono si ha quando le corde hanno la stessa lunghezza (rapporto 1/1); l'ottava quando una corda è lunga la metà dell'altra (rapporto 1/2); la quinta, quando le lunghezze delle corde stanno tra loro come 2 stà a 3 (rapporto 2/3); la quarta, quando le lunghezze stanno tra loro come 3 stà a 4 (rapporto 3/4). Così, pizzicando una corda tesa si ottiene una nota; pizzicandone una ugualmente tesa e lunga la meta della prima, si ottiene una nota consonante, situata un'ottava sopra la nota precedente; pizzicandone una che sia lunga i 6/5 di una corda che produca la nota «do» si ottiene «la»; pizzicandone una che ne sia lunga i 4/3 si ottiene «sol»; una lunghezza pari a 3/2 da «fa», e così via.
Ma, si chiesero i pitagorici, se l'armonia musicale si può esprimere coi numeri, perchè lo stesso non dovrebbe accadere per l'intero cosmo? E conclusero che tutti gli elementi dell'universo dovessero le loro proprietà alla natura dei numeri. Per esempio, le osservazioni astronomiche suggerivano che anche i moti dei corpi celesti fossero estremamente regolari, e sottoposti a un ordine ben preciso. Questo portò al concetto dell'«armonia delle sfere», l'idea che nei loro regolari movimenti, anche i corpi celesti producessero una musica armoniosa.
Il concetto dell'«armonia delle sfere» fù rielaborato, più di venti secoli dopo, dal famoso astronomo Keplero. Avendo, nel corso della vita, visto coi propri occhi le sofferenze e gli orrori della guerra, Keplero conduse che in realta la Terra produceva due note: «mi», come miseria («sventura» in latino) e «fa» per fames («indigenza»). Nelle parole dell'astronomo: «La Terra canta MI FA MI, così che anche dalle sillabe possiamo indovinare che a regnare in questa nostra dimora sono Sventura e Indigenza».
Forse a causa dei semplici rapporti armonici scoperti nella musica, 1/2, 2/3, 3/4 eccetera, i pitagorici svilupparono un particolare interesse per la differenza tra numeri pari e dispari. I numeri dispari erano da loro associati agli attributi della virilità e, non senza pregiudizio maschilista, alla luminosità e alla bontà, mentre, ovviamente, i numeri pari erano associati agli attributi della femminilità, dell'oscurità e del male.
A parte i ruoli che assegnarono ai numeri pari e dispari in generale, i pitagorici attribuirono specialì proprietà ad alcuni numeri particolari. L'l, per esempio, era considerato il progenitore di tutti i numeri, e perciò non era ritenuto un numero. Si riteneva inoltre che caratterizzasse la ragione. Geometricamente, 1 era rappresentato dal punto, a sua volta considerato il progenitore di tutte le dimensioni dello spazio.
Il numero 2 era il primo numero femminile, e anche il numero dell'opinione e della divisione. Idee abbastanza simili trovano espressione nella teoria cosmologico-religiosa cinese dello Yin e dello Yang, nella quale lo Yin rappresenta il principio femminile e negativo, associato a proprietà come la passività e l'oscurità, mentre lo Yang è il principio maschile associato alla luminosità. L'originaria identificazione del 2 con la femminilità e del 3 con la virilità puo essere stata rafforzata dall'aspetto dei seni femminili e dei genitali maschile. Nella vita di tutti i giorni, la divisione in due categorie di vari aspetti dell'esperienza è estremamente comune: buono e cattivo, alto e basso, destra e sinistra, e così via. Geometricamente, 2 era espresso dalla linea, determinata da due punti, che ha una dimensione.
Il 3 era considerato il primo vero numero maschile, e anche il numero dell'armonia, combinando l'unita (il numero 1) e la divisione (il numero 2). Per i pitagorici, 3 era in un certo senso il primo numero reale, avendo un «inizio», un «mezzo» e una «fine» (diversamente da 2, che non possiede una parte intermedia). L'espressione geometrica del 3 era il triangolo, determinate da tre punti non giacenti su una retta, ed esteso in due dimensioni.
Per i pitagorici, 4 era il numero della giustizia e dell'ordine. Sulla superficie della Terra, i quattro venti, o direzioni, fornivano agli uomini il necessario orientamento per individuare le coordinate dello spazio. Geometricamente, quattro punti che non giacciono sullo stesso piano formano un tetraedro (una piramide con quattro facce triangolari, il cui volume si estende nelle tre dimensioni.
Un'altra considerazione che agli occhi dei pitagorici conferiva uno status speciale al numero 4 era l'estrema importanza attribuita al numero 10, la «santa tetractys». Il 10 era il numero da loro più riverito, perchè considerate una rappresentazione del cosmo nella sua interezza. Il fatto che la somma dei primi 4 interi (1 + 2 + 3 + 4) sia appunto 10 collegava strettamente 10 e 4. Nello stesso tempo, questa relazione significava che 10 riuniva i numeri che rappresentavano non solo tutte le dimensioni spaziali, ma anche le proprieta fondamentali dell'unicità (1), della polarita (2), dell'armonia (3) e della realtà spaziale/materiale (4). II 10 era quindi il numero del tutto.
Il 6 era il primo numero perfetto, e il numero della Creazione. L'aggettivo perfetto era usato per i numeri esattamente uguali alla somma di tutti i loro divisori. E' questo il caso di 6, dato che i suoi divisori sono 1, 2 e 3 e 1 + 2 + 3 = 6. Il successive numero perfetto è 28, i cui divisori sono 1, 2, 4, 7 e 14; il terzo e 496, i cui divisori sono 1, 2, 4, 8, 16, 31, 62, 124 e 248. Si vede che i numeri perfetti crescono rapidamente, e infatti il nono della serie contiene già trentasette cifre. II numero 6 è anche il prodotto del primo numero «femminile» (2) e del primo numero «maschile» (3). Alcuni commentatori della Bibbia hanno considerate anche 28 un numero fondamentale del Sommo Architetto, pensando tra l'altro ai 28 giorni del ciclo lunare.
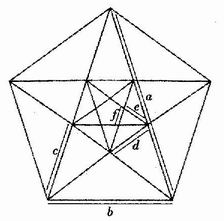 Il numero 5 ci conduce alle origini del rapporto aureo. Il 5 era considerate l'unione del primo numero femminile e del primo numero maschile, e come tale, il numero dell'amore e del matrimonio. Sembra che i pitagorici avessero adottato il pentagramma (la Stella a cinque punte) quale simbolo della loro confraternità, e che lo chiamassero «Salute». Il pentagramma è anche strettamente legato al pentagono regolare, la figura piana con cinque lati e cinque angoli uguali. Collegando tutti i vertici del pentagono tramite diagonali si ottiene un pentagramma. Inoltre, le diagonali formano vicino al centro un pentagono regolare più piccolo. Ovviamente, il procedimento può essere ripetuto in questo pentagono, producendo un secondo pentagramma e un terzo pentagono, in una progressione che può continuare all'infinito.
Il numero 5 ci conduce alle origini del rapporto aureo. Il 5 era considerate l'unione del primo numero femminile e del primo numero maschile, e come tale, il numero dell'amore e del matrimonio. Sembra che i pitagorici avessero adottato il pentagramma (la Stella a cinque punte) quale simbolo della loro confraternità, e che lo chiamassero «Salute». Il pentagramma è anche strettamente legato al pentagono regolare, la figura piana con cinque lati e cinque angoli uguali. Collegando tutti i vertici del pentagono tramite diagonali si ottiene un pentagramma. Inoltre, le diagonali formano vicino al centro un pentagono regolare più piccolo. Ovviamente, il procedimento può essere ripetuto in questo pentagono, producendo un secondo pentagramma e un terzo pentagono, in una progressione che può continuare all'infinito.
Le curiose proprietà di questa serie di figure non sono finite: osservando i segmenti via via più corti generati dal procedimento descritto, è facile dimostrare con considerazioni di geometria elementare che ogni segmento è minore del precedents di unfattore esattamente uguale al rapporto aureo). In altre parole, il rapporto a/b è uguale a Phi (Φ), il rapporto b/c è uguale a Φ eccetera. Ancora più importante è che il fatto di poter creare una serie di pentagoni e pentagrammi inseriti gli uni dentro gli altri proseguendo indefinitamente può essere usato per dimostrare rigorosamente che la diagonale e il lato del pentagono sono incommensurabili, ovvero che il rapporto delle loro lunghezze (pari a Φ) non può essere espresso come rapporto di numeri interi. Un altro modo di esprimere lo stesso concetto, è dire che la diagonale e il lato del pentagono non possono avere nessuna comune unità di misura, ossia, ancora, che non può esistere nessun segmento, per quanto corto, tale che la diagonale sia un multiple intero, e il lato un altro multiplo intero di quel segmento.
Numeri irrazionali
Quando Pitagora affermava che l'universo è governato dai numeri, si riferiva ai numeri interi e ai rapporti (o rationes) fra numeri interi, cioè alle frazioni. I numeri interi e i numeri frazionali sono noti come numeri razionali. Un numero irrazionale, ed è questo l'aspetto che appariva orribile a Pitagora, è un numero che non è né intero né frazionario. Infatti i numeri irrazionali sono così strani da non poter essere scritti in termini decimali, neppure in termini di decimali periodici. Un decimale periodico come 0,111111... è ancora un numero abbastanza semplice ed equivale alla frazione 1/9. Il fatto che il numero 1 si ripete per sempre significa che il decimale ha una struttura molto semplice e regolare. Questa regolarità, nonostante continui all'infinito, comporta che il decimale possa essere riscritto in termini frazionari. Se invece cercate di esprimere un numero irrazionale in forma decimale finirete per avere un numero che continua per sempre senza una struttura regolare o coerente.
Il concetto di numero irrazionale fu una novità terribile. I matematici stavano guardando oltre i numeri interi e quelli frazionari ai quali erano abituati e ne stavano scoprendo o forse inventando di nuovi.
Il più famoso numero irrazionale è 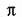 . A scuola talvolta lo si approssima con 3,14, ma il vero valore di n è più vicino a 3,14159265358979323846, ma anche questa cifra è soltanto un'approssimazione. Non si può mai scrivere esattamente il valore di n, perché i decimali proseguono all'infinito senza alcuno schema regolare. Una meravigliosa caratteristica di questo suo sviluppo casuale è che lo si può calcolare con un'equazione che è estremamente regolare:
. A scuola talvolta lo si approssima con 3,14, ma il vero valore di n è più vicino a 3,14159265358979323846, ma anche questa cifra è soltanto un'approssimazione. Non si può mai scrivere esattamente il valore di n, perché i decimali proseguono all'infinito senza alcuno schema regolare. Una meravigliosa caratteristica di questo suo sviluppo casuale è che lo si può calcolare con un'equazione che è estremamente regolare:
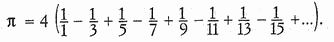
Calcolando solo i primi termini si può ottenere un valore molto approssimativo di 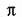 , ma calcolandone sempre di più l'approssimazione ottenuta si fa sempre più accurata. Anche se conoscere n fino a 39 cifre decimali è sufficiente per calcolare la circonferenza dell'universo con un margine di errore pari soltanto al raggio di un atomo di idrogeno, questo non ha trattenuto gli scienziati dal calcolare con il computer n fino al maggior numero possibile di decimali. Il record attuale è detenuto da Yasumasa Kanada dell'Università di Tokyo che ha calcolato con il computer n fino a sei miliardi di decimali nel 1996. Recentemente si è sparsa la voce che i fratelli russi Chudnovsky a New York avessero calcolato n fino a otto miliardi di decimali e che intendessero raggiungere il trilione. È da osservare che se Kanada o i fratelli Chudnovsky proseguissero i loro calcoli finché i loro computer esaurissero tutta l'energia dell'universo, non potrebbero comunque stabilire il valore esatto di n. È facile capire perché Pitagora abbia tramato per nascondere l'esistenza di questo mostro matematico.
, ma calcolandone sempre di più l'approssimazione ottenuta si fa sempre più accurata. Anche se conoscere n fino a 39 cifre decimali è sufficiente per calcolare la circonferenza dell'universo con un margine di errore pari soltanto al raggio di un atomo di idrogeno, questo non ha trattenuto gli scienziati dal calcolare con il computer n fino al maggior numero possibile di decimali. Il record attuale è detenuto da Yasumasa Kanada dell'Università di Tokyo che ha calcolato con il computer n fino a sei miliardi di decimali nel 1996. Recentemente si è sparsa la voce che i fratelli russi Chudnovsky a New York avessero calcolato n fino a otto miliardi di decimali e che intendessero raggiungere il trilione. È da osservare che se Kanada o i fratelli Chudnovsky proseguissero i loro calcoli finché i loro computer esaurissero tutta l'energia dell'universo, non potrebbero comunque stabilire il valore esatto di n. È facile capire perché Pitagora abbia tramato per nascondere l'esistenza di questo mostro matematico.
I Poliedri di Platone
Nel Timeo, Platone non esita ad affrontare l'immensa questione delle origini! e del funzionamento del cosmo. In tale contesto egli avanza l'ipotesi che la struttura della materia si fondi sui cinque solidi regolari (o poliedri), già indagati dai pitagorici e poi, in modo molto più sistematico, da Teeteto (c. 417 - c. 369 a.C.). I cinque solidi platonici sono contraddistinti dalle seguenti proprietà: sono gli unici solidi le cui facce sono tutte equilatere e uguali tra loro; ciascun solido e circoscritto da una sfera (in modo che tutti i suoi vertici si trovino sulla superficie di quest'ultima).
I solidi platonici sono: il tetraedro, con quattro facce triangolari, (1); il cubo, con sei facce quadrate, (2); l'ottaedro, con otto facce triangolari, (3); il dodecaedro, con dodici facce pentagonali, (4); e l'icosaedro, con venti facce triangolari, (5).
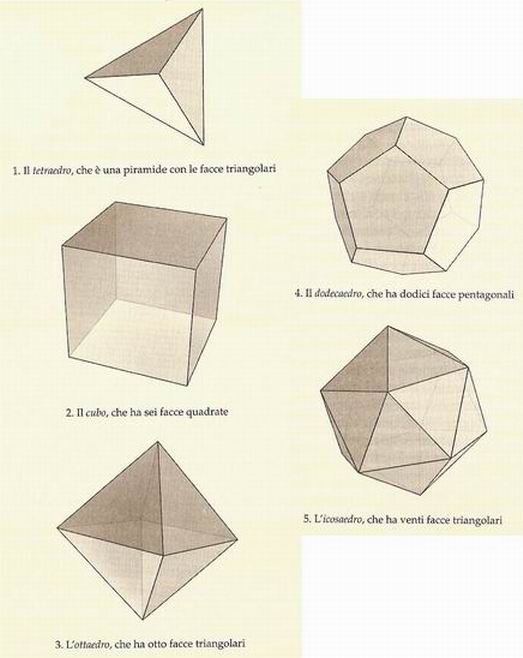
Platone fuse la teoria di Empedocle (c. 490 - c. 430 a.C.) che i quattro element! fondamentali della materia fossero la terra, l'acqua, l'aria e il fuoco, con la concezione di Democrito di Abdera (c. 460 - c. 370 a.C.), secondo il quale le componenti ultime dell'universo erano il vuoto e alcune particelle materiali non ulteriormente divisibili dette «atomi». Nella teoria «unificata» di Platone, ciascuno dei quattro elementi corrispondeva a un tipo diverso di particella fondamentale, rappresentata da uno dei solidi regolari. Secondo Platone, l'emento terra è legato allo stabile cubo, il fuoco, che «fà breccia*, al puntuto e semplice tetraedro, l'aria alla «mobile» forma dell'ottaedro e l'acqua allo sfaccettato icosaedro. Il quinto solido, il dodecaedro, fù collegato da Platone all'universo nel suo insieme; o, per usare le sue parole, il dodecaedro sarebbe la forma «usata dalla divinità per ricamare le costellazioni sull'insieme dei cieli». Per questo Salvador Dali ha immaginato un grande dodecaedro fluttuante sul tavolo del banchetto nel Sacramento dell'Ultima Cena.
L'assenza di un elemento associato al dodecaedro non fù accettata da tutti i seguaci di Platone, alcuni dei quali supposero l'esistenza di una quinta sostanza fondamentale. Aristotele, per esempio, introdusse l'etere quale elemento costitutivo dei corpi celesti, ma presente nell'intero universo in qualità di «quinta essenza» cosmica. Pervadendo ogni altra materia, la quinta essenza permetteva il verificarsi del movimento e di ogni altro cambiamento in armonia con le leggi naturali.
Il rapporto aureo occupa una posizione importante nelle dimensioni e nella simmetria di alcuni poliedri platonici. In particolare, un dodecaedro con lato unitario (il lato e il segmento rettilineo che due facce vicine hanno in comune) ha una superficie complessiva la cui area e pari a 15Φsqrt(3-Φ), e un volume pari a 5(Φ)3 / (6- 2Φ) In modo simile, un icosaedro di lato unitario ha un volume uguale a 5(Φ)5/6.
La simmetria dei poliedri platonici si manifesta con altre curiose proprietà. Per esempio, il cubo e l'ottaedro hanno lo stesso numero di spigoli (dodici), ma il numero di facce e di vertici risulta invertito (il cubo ha sei facce e otto vertici, l'ottaedro otto facce e sei vertici). Lo stesso accade col dodecaedro e l'icosaedro: entrambi hanno trenta spigoli, ma il dodecaedro ha dodici facce e veti vertici, mentre il contrario si verifica nell'icosaedro. Queste somiglianze e simmetrie dei solidi platonici permettono interessanti riproduzioni di un poliedro nel suo «reciproco». Congiungendo i centri di tutte le facce di un cubo si ottiene un ottaedro, così come congiungendo i centri di tutte le facce di un ottaedro si otriene un cubo. Lo stesso procedimento si può usare per riprodurre un icosaedro in un dodecaedro, e viceversa, e il rapporto delle lunghezze degli spigoli dei due solidi (quello esterno e quello riprodotto) è dato da una formula contenente, ancora una volta, il rapporto aureo: Φ2 / sqrt(5). Il tetraedro è autoriproducibile: congiungendo i centri delle facce di un tetraedro si ottiene un altro tetraedro.
(Tratto da "La sezione aurea" di Mario Livio - 2003 Rizzoli e da "L'ultimo teorema di Fermat" di Simon Singh - 1999 BUR Saggi)


