Fin qui abbiamo parlato degli uomini che crearono il calcolo differenziale. Ma di che cosa si tratta, esattamente?
Il calcolo differenziale da la possibilità di descrivere e analizzare il moto e il cambiamento. Non qualsiasi tipo di moto o di cambiamento, però: occorre un modello che descriva il suo verificarsi. In termini concreti, il calcolo differenziale è un insieme di tecniche per la manipolazione di modelli (la parola calculus, in latino, significa «sassolino». I primi sistemi di conteggio comportavano infatti la manipolazione di sassi).
L'operazione fondamentale del calcolo differenziale è nota come «differenziazione»; il suo scopo è dì ottenere la velocità di variazione di una certa grandezza. Per farlo, occorre darne il valore, la posizione o la traiettoria esprimendoli con una formula appropriata. L'operazione di differenziazione agisce allora su quella fòrmula per produrne un'altra, che rappresenta la velocità di variazione. Pertanto, la differenziazione è un processo che trasforma formule in altre formule.
Supponiamo, per esempio, che un'automobile viaggi lungo una strada e che la distanza coperta, che chiameremo x vari nel tempo t, secondo la formula seguente:
x = 5*t2 + 3 * t
Allora, applicando il calcolo differenziale, in qualsiasi istante t la velocità s (ossia il cambiamento della posizione in rapporto al tempo) è data dalla formula
s= 10*t + 3
Si noti che in questo esempio la velocità dell'automobile non è una costante: essa varia invece nel tempo, proprio come varia la distanza. Il processo di differenziazione può essere applicato una seconda volta per trovare l'accelerazione (la variazione della velocità in rapporto al tempo).
a=10
che, in questo caso, è una costante.
I fondamentali oggetti matematici ai quali si applica il processo dì differenziazione sono chiamati «funzioni». In assenza del concetto di funzione, non può esserci calcolo. Proprio come l'addizione aritmetica è un'operazione eseguita sui numeri, la differenziazione è un'operazione eseguita sulle funzioni.
Ma che cosa è esattamente una funzione? La risposta più semplice è questa: in matematica, una funzione è "una regola grazie alla quale, dato un numero, è possibile calcolarne un altro (in termini rigorosi, questo in realtà è un caso particolare, tuttavia è sufficiente per comprendere il meccanismo del
calcolo).
Per esempio, una formula polinomiale come
y = 5x3 - 10x2 + 6x + 1
determina una funzione. Dato un qualsiasi valore di x, la formula dice come calcolare un corrispondente valore di y.
Per esempio, se x = 2, possiamo calcolare y come segue:
y = (5 x 23) - (10 x 22) + (6 x 2) + 1 = 40 - 40 + 12 + 1 = 13
Altri esempi sono quelli delle funzioni trigonometriche y = sen x, y = cos x:, y = tg x. In questi casi, non esiste un modo semplice per calcolare il valore di y come abbiamo fatto nel caso dell'espressione polinomiale. La loro comune definizione è data in termini di rapporto dei diversi lati dei triangoli rettangoli, ma si tratta di definizioni che si applicano solo quando x è un angolo minore di 90°. Il matematico definisce la funzione tangente in termini di seno e coseno come segue:
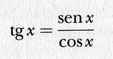
e definisce le funzioni seno e coseno per mezzo di somme infinite:
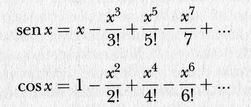
Per comprendere queste formule occorre sapere che, come abbiamo visto nel capitolo 3, per ogni numero naturale n, n! (che si legge « n fattoriale ») è uguale al prodotto di tutti i numeri, da 1 a n compreso. Per esempio, 3! = 1x2x3 = 6. Occorre anche capire che quei tre puntini a destra dell'espressione significano che la serie continua seguendo lo stesso modello all'infinito. Le somme infinite per sen x e cos x hanno sempre un valore finito, e possono essere manipolate, in linea di massima, come espressioni polinomiali finite.
Un ulteriore esempio è quello della funzione esponenziale
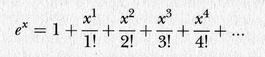
Anche in questo caso, questa somma infinita ha sempre un valore finito, e può essere manipolata come un'espressione polinomiale finita. Ponendo x = 1, si ottiene
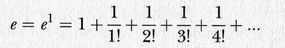
La costante matematica e, ossia il valore di questa serie infinita, è un numero irrazionale. La sua espansione decimale comincia così: 2,71828.
La funzione inversa di ex, ossia la funzione che inverte esattamente l'effetto di ex è particolarmente importante: si tratta infatti del logaritmo naturale, ln(x). Se si prende un numero a e si applica la funzione ex così da ottenere il numero b = ea, applicando successivamente a b la funzione ln(x) si ottiene di nuovo a, poiché a = ln(b).
Come calcolare le pendenze, ovvero: la derivata
Le formule algebriche - come le espressioni polinomiali o le somme infinite che definiscono le funzioni trigono-metriche o esponenziali - sono un modo molto preciso di descrivere un certo tipo dì modello astratto. In questo caso, il modello consiste nell'associazione fra due valori numerici: quello assunto inizialmente dalla x (la variabile indipendente o argomento) e quello assunto dalla y (il valore risultante della variabile dipendente). In molti casi questo modello può essere rappresentato graficamente. Il grafico di una funzione mostra, già a un rapido sguardo, il modo in cui la variabile y è legata alla variabile x.
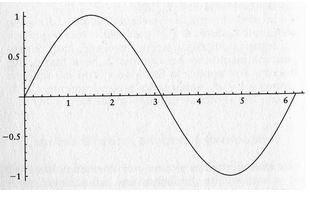
Nel caso della funzione sen x, per esempio, partendo da O, a mano a mano che x aumenta, aumenta anche y finché, a partire da un punto prossimo a x — 1,5 (il valore esatto è x = p/2), y comincia a diminuire, per diventare negativo in prossimità di x = 3,1 (precisamente, quando x =
p); y continua a diminuire fino a circa x — 4,7 (precisamente 3p/2) e infine riprende a salire.
Il compito dì fronte al quale si trovarono Newton e Leibniz era questo: Come si fa a trovare la velocità di variazione di una funzione come sen x? In altre parole: come si fa a trovare la velocità di variazione di y rispetto a x? In termini grafici, questo problema equivale a trovare la pendenza della curva, a chiedersi, insomma, quanto essa sia ripida. La difficoltà sta nel fatto che la [pendenza non è costante; a un certo punto la curva sale impennandosi (grande pendenza positiva), in altri tratti é quasi orizzontale (pendenza prossima allo zero) e in filtri ancora precipita (grande pendenza negativa).
Riassumendo, proprio come il valore di y dipende da quello di x, la pendenza in ogni punto della curva dipende anch'essa dal valore di x. In altre parole, la pendenza di una funzione è a sua volta una funzione, una funzione secondaria. La domanda ora è: data la formula di una funzione, la quale descrive il modello che stabilisce la relazione fra x e y,è possibile trovare una formula per descrivere il modello che mette in relazione x alla pendenza della curva?
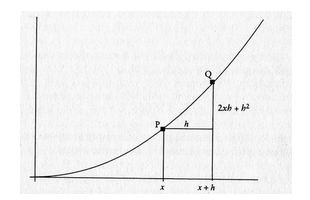
Il passo cruciale mosso qui da Newton e da Leibniz consistette nello spostare l'attenzione da una situazione essenzialmente statica (riguardante la pendenza della curva in un punto particolare P) al processo dinamico in cui la pendenza della curva viene approssimata dalle pendenze delle rette tracciate successivamente a partire da P. Fu proprio osservando i modelli numerici e geometrici emergenti da questo processo di approssimazione che Newton e Leibniz riuscirono a risolvere il problema.
In effetti, sebbene Newton e Leibniz fossero pervenuti alla soluzione corretta, occorsero due secoli perché i matematici riuscissero a fornire una spiegazione completa del perché il loro metodo funzionasse. Per farlo, dovettero elaborare una rigorosa teoria matematica dei processi di approssimazione, cosa che né Newton, né Leibniz erano stati in grado di fare. Fu solo nel 1821 che Augustin-Louis Cauchy sviluppò il concetto fondamentale di «limite» (di una quantità variabile), di cui qualche anno dopo Karl Weierstrass diede una definizione formale. Solo allora il calcolo infinitesimale fu collocato su basi solide.
Questo processo, ovvero il passaggio dalla formula di una curva alla formula della sua pendenza è noto come differenziazione (il nome riflette l'idea di prendere piccole differenze delle x e delle y e di calcolare le pendenze delle rette risultanti). La funzione della pendenza è denominata derivata della funzione iniziale (dalla quale essa effettivamente « deriva »).
Nell'esempio che abbiamo esaminato, la funzione 2x è la derivata della funzione x2. Analogamente, 3x2 è la derivata della funzione x3, e in generale la derivata della funzione xn per qualsiasi numero naturale n è nx(n-1). Dimostrando quel genere di simmetria che spesso si riscontra in matematica, la derivata di sen x risulta essere cos x - cosicché cos x fornisce la pendenza di sen x in ogni punto della curva; in modo quasi altrettanto elegante, la derivata di cos x è -sen x, in cui c'è solo quel segno meno a infrangere una simmetria perfetta. Ancor più bello, la derivata dì ex è la stessa ex: ciò significa che ex fornisce la propria stessa pendenza in ogni punto. È questa la sola funzione con questa proprietà. La derivata di ln x è 1/x.
La potenza dell'invenzione di Newton e Leibniz stava nel fatto che il numero di funzioni dìfferenziabili era molto aumentato dallo sviluppo di un calculus, ovvero di una serie di regole per differenziare funzioni complicate. Lo sviluppo di queste tecniche rende anche conto dell'enorme, immediato successo del metodo in varie applicazioni, e questo sebbene esso dipendesse da metodi di ragionamento all'epoca non pienamente compresi. Si sapeva che cosa fare, anche se nessuno avrebbe saputo dire perché funzionasse (negli odierni corsi di calcolo infinitesimale, sono molti gli studenti che vivono un'esperienza simile).
Portare il calcolo infinitesimale in una dimensione superiore
Il calcolo infinitesimale si applica a funzioni in una sola variabile, ossia a funzioni che producono un valore di y prendendo in considerazione una singola variabile x. Tali funzioni possono essere rappresentate geometricamente per mezzo di un grafico bidimensionale, in genere una curva. Le stesse idee, d'altra parte, sono applicabili anche in situazioni più generali. In particolare, il calcolo infinitesimale può essere sviluppato per funzioni a due variabili, z = f(x,y), la cui interprelazione geometrica è una superfìcie, là dove z rappresenta l'altezza della superficie stessa al di sopra del piano xy, in corrispondenza del punto di coordinate (x,y), o anche per funzioni a tre o più variabili.
Per funzioni a tre variabili, del tipo v = f(x,y,z) non esiste una semplice rappresentazione geometrica, tuttavia sono numerosi i fenomeni fisici comuni che si presentano in questa forma. Per esempio, (x,y,z) potrebbero essere le coordinate di un elicottero in volo e u = g(x,y,z) la sua velocità quando si trova nel punto di latitudine x, longitudine y e altitudine z. Oppure, w = T(x,y,z) potrebbe essere la temperatura dell'atmosfera terrestre nel punto di latitudine x, longitudine y e altitudine z.
Nel caso della funzione di due variabili, non esiste qualcosa di simile a un'unica velocità di variazione in un punto. La velocità dipende infatti dalla dirczione del moto. Supponiamo, per esempio, di essere a metà strada nell'ascesa di una montagna. Se continuiamo a puntare direttamente verso la cima, la pendenza della nostra traiettoria sarà un numero positivo, probabilmente grande. Ma se decidiamo di smettere di salire e ci limitiamo a camminare a mezza costa rimanendo sempre alla stessa altezza, la pendenza sarà nulla. In altre parole, la pendenza della traiettoria nel punto in cui ci troviamo dipende dal percorso che desideriamo imboccare il. da questo punto in avanti. Allo stesso modo, per funzioni in tre o più variabili, la pendenza in ogni punto dipende dalla dirczione del moto. Un elicottero, per esempio, potrebbe avere velocità verticale nulla, un'elevata velocità orizzontale e una velocità più bassa lateralmente, verso destra.
Ora, per analizzare il movimento in due o più dimensioni, non occorre calcolare la velocità di variazione (ossia la pendenza) in tutte le direzioni possibili. Basta conoscere la velocità di variazione nelle direzioni corrispondenti agli assi, ossia, nel caso di una funzione z = f(x,y), la velocità di variazione nelle direzioni x e y e nel caso di una funzione v = g(x,y,z), la velocità di variazione nelle direzioni x, y e z.
Un possibile esempio, del quale faremo ben presto uso è il seguente: supponiamo di voler descrivere il moto di un granello di polvere trasportato da un fluido in movimento. Il moto del granello potrebbe essere complicatissimo, giacché esso viene lanciato dapprima in una dirczione, poi in un'altra e, se a volte si muove seguendo una traiettoria abbastanza rettilinea, altre volte, quando la corrente prende il sopravvento, descrive delle spirali. In ogni istante di tempo t, possiamo specificare l'esatta posizione del granello di polvere dando le sue tre coordinate x, y e z (rispetto a un sistema di riferimento prefissato). Allo stesso modo, possiamo specificare il suo moto al tempo t descrivendo come esso si muove in ciascuna delle direzioni corrispondenti alle tre coordinate, per esempio calcolando la velocità di variazione della sua posizione nella dirczione degli assi x,y e z. (Quando facciamo questo servendoci del calcolo infinitesimale, otteniamo le cosiddette «derivate direzionali » riferite a x, y e z.)
Quest'idea di descrivere il moto nello spazio tridimensionale scomponendolo rispetto a ciascuna delle direzioni delle tre coordinate è alla base delle applicazioni di Eulero del calcolo infinitesimale al moto dei fluidi, applicazioni in seguito elaborate da Navier e Stokes. Ecco qui l'idea generale.
Per semplicità, cominciamo con il caso dì una funzione a due variabili z = f(x,y). Le velocità di variazione nelle direzioni degli assi vengono calcolate prendendo !a sezione trasversale appropriata della figura geometrica interessata - nel caso di una funzione z = f(x, y) una superficie - e applicando a quella sezione trasversale i metodi standard del calcolo infinitesimale per funzioni a una sola variabile.
Per indicare che la differenziazione viene eseguita in B»una dirczione particolare, i matematici usano una notazione leggermente modificata. Per una funzione y =f(x), nella quale esiste solo una variabile indipendente x, la velocità di variazione di y nel punto x è indicata da dy/dx. Per una funzione z=f(x,y), in cui compaiono due variabili indipendenti x e y, la velocità di variazione di z rispetto a x è indicata da dz/dx, e la velocità di variazione rispetto a y è indicata con dz/dy. I La quantità (o se preferite la formula) dz/dx è denominata derivata parziale di z rispetto a x, e dz/dy è denominata derivata partiate dì z rispetto a y. Pertanto, dz/dx è la pendenza che si incontra quando ci si muove lungo la superfìcie parallelamente all'asse x; dz/dy è la pendenza che si incontra quando ci si muove invece parallelamente all'asse y.
Per esempio, nel caso della funzione
z = x2 - 3xy - y5
Allo stesso modo, per una funzione v =f(x,y,z), il moto (o la variazione) di v in un qualsiasi punto di coordinate (x,y,z) può essere determinato dalle tre derivate parziali dv/dx, dv/dy, dv/dz, che danno la velocità di variazione del valore della funzione rispetto a ciascuno dei tre assi. In questo caso, ovviamente, non esiste una visualizzazione geometrica che possa soccorrerci mostrandoci la funzione.
Tutto questo fu elaborato grazie al contributo di molti matematici, negli anni successivi all'invenzione del calcolo infinitesimale da parte di Newton e Leibniz. E a questo punto, entrò in scena Daniel Bernoulli.
Da sfere e pianeti al flusso dei liquidi.
Daniel Bernoulli proveniva da una numerosa famiglia di matematici svizzeri di grande talento, vissuti nel diciottesimo secolo. Suo padre, Johann, era professore di matematica all'università di Basìlea. Padre e figlio furono molto influenzati dal metodo del calcolo infinitesimale, ed entrambi contribuirono a sviluppare la nuova tecnica. All'epoca, il calcolo era usato (nella concezione di Newton) per studiare il moto continuo di oggetti solidi come i pianeti, oppure {nella concezione di Leibniz) per studiare la pendenza, in continua variazione, di funzioni geometriche continue. Daniel Bernoulli cercò invece di applicare il metodo al moto continuo dei fluidi, termine che per uno scienziato indica liquidi o gas. A prima vista, si trattava di un problema molto diverso.
Il moto continuo analizzato da Newton e Leibniz era quello di un singolo oggetto discreto (un pianeta o una particella per Newton; la punta che traccia un grafico o una superficie per Leibniz). Nel caso del fluido in movimento, però, non solo il moto, ma anche il materiale è continuo. L'idea di come accostarsi a questo problema era abbastanza evidente. Proprio come il solito calcolo infinitesimale considerava il moto continuo costituito da spostamenti discreti infinitesimamente piccoli e infinitesimamente vicini nel tempo, allo stesso modo Bernoulli considerò il fluido continuo costituito da regioni discrete (o «blobs») infinitesimamente piccole, infinitamente vicine, ciascuna delle quali poteva (in linea di principio) essere manipolata usando i metodi di Newton e Leìbniz.
Un altro modo di pensare al problema è mirare a scrivere equazioni che descrivano la traiettoria di una qualsiasi particella di polvere - « un punto infinitesimo » - localizzata in un qualsiasi punto particolare del fluido. Questo richiede la manipolazione di due insiemi di infinitesimi.
Dapprima, il moto di ciascuna particella infinitesima viene considerato come una sequenza di fotogrammi immobili. Questo è il calcolo infinitesimale classico (per il moto continuo di un oggetto, dove il moto viene affrontato come una sequenza temporale di situazioni statiche.
Poi c'è da considerare la variazione geometrica infinitesima fra la traiettoria di una particella e quella di un'altra particella infinitesimamente vicina alla prima. La difficoltà stava nel manipolare simultaneamente entrambi i tipi di infinitesimi: quelli temporali per il movimento di ciascuna particella e quelli geometrici per il fluido. Bernoulli investì nell'impresa gran parte della sua vita adulta, e ci riuscì. Nel 1738 pubblicò i suoi risultati nel libro Hydrodynamics. L'idea fondamentale fu quella di assumere che la soluzione fosse un cosiddetto campo vettoriale. Intuitivamente, si tratta di una funzione di tre variabili x, y, z che ci da velocità e direzione del flusso del fluido in ogni suo punto di coordinate (x,y,z).
Fra i risultati ai quali Bernoulli pervenne nel suo libro c'è un'equazione che dimostra quanto segue: quando scorre su una superfìcie, un fluido esercita sulla superficie stessa una pressione che diminuisce all'aumentare della sua velocità. Perché vale la pena di parlarne? Perché l'equazione di Bernoulli (questo è il nome con cui oggi essa è nota) sta alla base dell'aeronautica moderna.
Per dirla in termini semplici, l'equazione di Bernoulli parla di ciò che tiene in aria un aeroplano.
Partendo dal lavoro di Bernoulli, Eulero formulò le equazioni che descrivono il moto di un fluido non viscoso soggetto a determinate forze, senza però riuscire a risolverle. In seguito, Navier e Stokes modificarono le equazioni di Eulero in modo da tener conto della viscosità (ossia dell'attrito presente all'interno del fluido). Le equazioni risultanti sono note come equazioni di Navier-Stokes.
Sebbene queste equazioni possano essere risolte nell'ipotetico caso bidimensionale di un film fluido planare infinitamente sottile, non è noto se esista una soluzione nel caso tridimensionale (peraltro più realistico). Si noti che qui il problema non è: «Qual è la soluzione?». E ben più fondamentale: non sappiamo nemmeno se una soluzione esista!
(Tratto da "I problemi del millennio - Keith Devlin- 2002 Longanesi & C.)


