Sin dagli antichi greci, la matematica aveva accumulato in misura sempre maggiore teoremi e verità e sebbene gran parte di essi fosse stata rigorosamente dimostrata, i matematici temevano che alcuni, come la legge della tricotomia, fossero entrati di soppiatto nel sapere matematico senza essere stati adeguatamente esaminati. Alcune idee erano diventate parte del patrimonio comune e tuttavia nessuno era davvero certo di come fossero state originariamente dimostrate e neppure se davvero lo fossero state. I logici decisero di dimostrare ogni teorema dai primi principi.

Tuttavia ogni verità doveva essere dedotta da altre verità. A loro volta queste verità dovevano essere dimostrate ricorrendo ad altre verità ancor più fondamentali e così via. Alla fine i logici si trovarono dinanzi a pochi enunciati essenziali, talmente fondamentali da non poter essere a loro volta dimostrati. Queste assunzioni basilari sono gli assiomi della matematica.

Un esempio degli assiomi è la legge commutativa di addizione, che recita semplicemente che, per ogni numero m e n,

m + n = n + m.

Questo e pochi altri assiomi sono considerati evidenti per sé e possono essere facilmente verificati applicandoli a numeri particolari. Fino ad oggi gli assiomi hanno superato ogni verifica e sono stati accettati come il fondamento della matematica. La sfida per i logici era di ricostruire tutta la matematica a partire da questi assiomi.

Un'intera legione di logici prese parte al processo lento e faticoso di ricostruzione del corpo immensamente complesso della conoscenza matematica usando soltanto un numero minimo di assiomi. L'idea era di consolidare ciò che i matematici pensavano già di sapere impiegando solo i criteri logici più rigorosi. Oltre a purificare ciò che era noto, con questa impostazione estremamente rigorosa si sperava anche di gettare luce su problemi ancora irrisolti, tra i quali l'Ultimo Teorema di Fermat.

Il programma era diretto dalla figura più eminente dell'epoca, David Hilbert.

Hilbert riteneva che in matematica tutto potesse e dovesse essere dimostrato a partire da assiomi fondamentali. Il risultato doveva essere di dimostrare in maniera definitiva i due elementi più importanti del sistema della matematica. In primo luogo la matematica dovrebbe essere in grado, almeno teoricamente, di rispondere a ogni singola domanda: si tratta dello stesso ethos di completezza che in passato aveva richiesto l'invenzione di nuovi numeri come i negativi e gli immaginari. In secondo luogo, la matematica dovrebbe essere esente da contraddizioni, ossia dopo aver dimostrato con un metodo che un enunciato è vero, non dovrebbe essere possibile dimostrare con un altro metodo che lo stesso enunciato è falso. Hilbert era persuaso che, assumendo soltanto pochi assiomi, sarebbe stato possibile rispondere a ogni questione matematica immaginabile senza tema di cadere in contraddizione.

L'8 agosto 1900 David Hilbert fece uno storico discorso al Congresso Internazionale dei Matematici a Parigi. Hilbert pose ventitré problemi di matematica irrisolti, che a suo giudizio erano della massima importanza e urgenza. Alcuni di essi erano relativi alle aree più generali della matematica, ma la maggior parte si concentrava sui fondamenti logici della materia. Hilbert aveva segnalato questi problemi per attirare l'attenzione del mondo matematico e per delineare un programma di ricerca. Hilbert voleva ottenere l'aiuto dei matematici per attuare la sua concezione di un sistema matematico libero dai dubbi e dalle incongruenze.

Nel corso dei due decenni seguenti i logici e i matematici cercarono di completare la costruzione di un edificio matematico privo di crepe, e quando Hilbert andò in pensione nel 1930 egli poteva aver fiducia che la matematica fosse ormai ben avviata sulla strada di recuperare la coerenza perduta. Il suo sogno di una logica coerente, abbastanza potente da rispondere a ogni domanda, stava in apparenza per avverarsi.

Ma nel 1931 uno sconosciuto matematico venticinquenne pubblicò uno scritto che avrebbe distrutto per sempre le speranze di Hilbert. Kurt Godel avrebbe costretto i matematici ad accettare l'idea che Ja matematica non poteva mai essere logicamente perfetta e nella sua opera era implicita l'idea che problemi come l'Ultimo Teorema di Fermat potevano persine rimanere insolubili.

Kurt Friedrich Godel nacque il 28 aprile del 1906 nella città di Brno, in Moravia. La sua famiglia era di etnia tedesca, e aveva vissuto in Cecoslovacchia e Austria per generazioni. Godel aveva un fratello, Rudolf, di quattro anni più grande di lui, al quale era molto affezionato.

Il padre di Kurt, anch'egli di nome Rudolf, era un uomo d'affari di successo, La madre di Kurt, Marianne Handschuh, veniva da una classe sociale più elevata di quella del marito, e aveva ricevuto un'ottima istruzione. Allevò i due ragazzi sperando che divenissero raffinati gentiluomini, versati nelle arti, nella musica e nelle lingue straniere. Kurt imparò diverse lingue; invece parlava raramente il ceco, la sua lingua madre, dal momento che la famiglia lo considerava meno raffinato del tedesco.

Molto presto Godel dimostrò una curiosità insaziabile nei confronti del mondo (chiedeva continuamente: "Perché?", tanto che i genitori cominciarono a chiamarlo "Der Herr Warum", Il Signor Perché). All'età di dieci anni iniziò a frequentare il ginnasio, dove studiò i classici, come pure le scienze e la matematica, per prepararsi all'università. Sorprendentemente, colui che era destinato a diventare uno dei più grandi matematici del secolo ricevette un giudizio "molto buono" in ogni materia tranne che in matematica, disciplina nella quale conseguì un più modesto "buono", come testimonia un documento del 1917.!

Sembra che i Godel non si siano mai curati dei cambiamenti che avevano luogo nel mondo che li circondava. Nel 1914 scoppiò la Prima guerra mondiale. I Godel vivevano vicino ai luoghi dove si era scatenata la violenza, ma non si può dire che il conflitto abbia sconvolto la loro vita in alcun modo. Il padre continuò a curare i suoi fiorenti affari; la madre continuò a godere della vita culturale di Brno e Vienna; i due figli continuarono la loro vita di sempre. La famiglia andava spesso in vacanza in località alla moda, un'abitudine che nemmeno la guerra riuscì a intaccare.

Nel 1924 Kurt terminò il ginnasio e si trasferì a Vienna per iscriversi all'università. Nei tre anni precedenti si era concentrato sullo studio della matematica, ma aveva mostrato grande interesse anche per la filosofia e la fisica. Coltivò questi interessi per tutta la vita, e dedicò molti anni a mettere insieme concetti relativi al mondo fisico con idee filosofiche e con le scoperte che aveva fatto in merito ai fondamenti della matematica.

A Vienna, in un ambiente intellettualmente stimolante Godel sviluppò le idee della sua famosa dissertazione e dei suoi articoli successivi, che cambiarono per sempre il volto della scienza. Una volta presa la direzione che lo conduceva verso i fondamenti della matematica e verso il lavoro di Cantor sull'infinito attuale, utilizzò la sua profonda inclinazione filosofica per porre domande di importanza essenziale come: che cos'è una dimostrazione? La dimostrazione di una proposizione è qualcosa che coincide con la verità della proposizione stessa? Una proposizione vera è sempre dimostrabile? Può un sistema limitato produrre la dimostrazione di qualcosa che va al di là del sistema?

Dato un qualunque sistema, concluse Godel, vi saranno sempre proposizioni che non potranno essere dimostrate all'interno di questo sistema. Anche se un teorema è vero, può essere matematicamente impossibile dimostrarlo. Questa è l'essenza del famoso teorema d'incompletezza. La mente umana, che esiste all'interno di un universo limitato, non può comprendere un'entità immensa che si estende oltre i confini del sistema.

Il teorema di Godel è in qualche modo correlato con il teorema di Cantor sulla non esistenza di un numero cardinale più grande di tutti gli altri. Cantor aveva dimostrato che, dato un insieme comunque grande, esiste un insieme ancora più grande: l'insieme di tutti i sottoinsiemi dell'insieme dato. Quindi, per ogni sistema infinito, c'è sempre un sistema infinito più grande,la cui cardinalità è maggiore di quella dell'insieme dato. All'interno di ogni sistema limitato, esistono entità che non possono essere comprese o raggiunte o dimostrate, e per comprendere queste entità dobbiamo spostarci a un sistema più grande; ma quando lo facciamo, ci imbattiamo in sistemi più grandi ed entità che esistono al di là di questi.

Possiamo cercare di illustrare in che modo un sistema può essere incompleto in relazione ad alcuni teoremi, che non sono dimostrabili all'interno del sistema limitato, per mezzo di un'analogia con un programma per l'elaborazione di testi. Supponete di star lavorando a un documento sullo schermo del vostro computer. Potete fare molte cose: per esempio, potete scrivere un testo, spostarne, tagliarne e incollarne le parti, inserirvi disegni o formule create con altre applicazioni. Ma non potete cancellare il documento sul quale state lavorando dall'interno di quello stesso documento. Per farlo (o per spostare il documento in un'altra cartella), dovete uscire dal documento, e fare questa operazione all'interno di un sistema più ampio.

Alcune idee o proprietà non sono viste o rappresentate all'interno di un dato sistema, e per comprenderle dobbiamo passare a un altro livello. Dal momento che, come ha mostrato Cantor, non esiste un livello "più alto", dato un qualunque sistema vi saranno sempre idee o proprietà che non possiamo capire o di cui non possiamo parlare all'interno di questo. Analogamente, ciò che è soltanto un essere umano non può mai comprendere Dio, perché qualunque sistema la mente umana possa utilizzare, ci sono proprietà che non possono essere pienamente comprese all'interno di quel sistema limitato. E, dal momento che Dio occupa tutti i sistemi di livello più alto, la limitata mente umana non potrà mai raggiungere questi livelli più alti e comprendere, quindi, il divino.

Per i matematici il teorema di Godel è stato ancora più importante di quanto lo sia stato per i filosofi. Godel ha insegnato loro che alcuni teoremi non possono mai essere dimostrati. Per molte ragioni, questa è un'idea sconvolgente. Lo scopo della matematica è costruire una struttura di verità: teoremi, lemmi e corollari, tutti costruiti passo dopo passo a partire da un insieme di principi base chiamati "assiomi", usando le leggi della logica. La dimostrazione del teorema di incompletezza ci ha fatto vedere che, pef quanto attentamente i matematici possano progettare un sistema logico di princìpi primi su cui costruire l'aritmetica, l'algebra, l'analisi e il resto della matematica, un tale sistema non può mai essere completo. In ogni sistema di questo tipo, vi saranno problemi che non potranno essere risolti. Il sistema conterrà sempre asserzioni indecidibili, indipendentemente dal fatto se queste asserzioni sono vere o false.

Sebbene Godei non sia diventato una celebrità internazionale nell'arco di una notte, molti compresero presto l'importanza dei risultati che aveva conseguito a soli ventisei anni. Godei annunciò quanto aveva dimostrato nel corso di un seminario tenuto all'Università di Vienna il giorno dopo aver discusso la sua dissertazione nel 1930.

Dopo aver dimostrato i risultati di cui abbiamo detto sopra, Godel rivolse il suo interesse all'ipotesi del continuo, un risultato che fino ad allora non era stato dimostrato. Un altro argomento che lo affascinava era il discusso assioma della teoria degli insiemi: l'assioma di scelta.

Ma dopo essersi cimentato con i concetti proibiti di alef e con quelli dell'infinito attuale, Godel (come Cantor diversi anni prima) iniziò a soffrire di problemi psichiatrici. Anche se non era mai stato tormentato da colleglli e non aveva nemici mortali del calibro di un Kronecker, iniziò a mostrare segni di squilibrio mentale molto simili a quelli di Cantor. Venne colpito dalla depressione e lentamente si convinse che qualcuno lo perseguitava. Cominciò a sospettare che qualcuno stesse tentando di avvelenarlo e nel giro di alcuni anni avrebbe chiesto a Adele, che nel frattempo era diventata sua moglie, di assaggiare il suo cibo prima che lui lo mangiasse. Con il progredire della malattia Godel si nutrì sempre meno, finché si lasciò morire di fame.

Nel 1934 venne nuovamente invitato a recarsi presso l'Institute for Advanced Studies, dove grandi matematici apprezzavano il suo genio. Il mondo stava cambiando rapidamente: sull'Europa si addensavano le nubi minacciose del nazismo. Come era già avvenuto durante la Prima guerra mondiale, Godel era ignaro degli odi e dei pericoli che lo circondavano, anche se, vivendo a Vienna, non poteva non sapere dell'ascesa al potere di Hitler in Germania.

Chiunque in quegli anni, nel momento in cui l'Europa stava per essere avvolta dalle fiamme dell'odio razziale e della violenza, avrebbe colto al volo l'opportunità di fuggire per andare a vivere negli Stati Uniti. Godel, però, sprofondato nel suo lavoro sui fondamenti della matematica, stava lentamente perdendo ogni contatto con la realtà. Soffriva di strani malesseri (mal di stomaco, difficoltà respiratorie e altri disturbi) che potevano essere reali o psicosomatici. Nell'estate del 1934 la sua malattia peggiorò e venne ricoverato in una clinica psichiatrica nei pressi di Vienna, dove trascorse diversi mesi.

Riprese a lavorare febbrilmente, nel tentativo di dimostrare che l'assioma di scelta è compatibile con gli altri assiomi della teoria degli insiemi.

Mentre il mondo attorno a lui andava in pezzi, Godel entrava e usciva dalle cllniche psichiatriche, e, ignorando gli inviti generosi che gli provenivano dagli Stati Uniti (non soltanto da Princeton, ma anche da altre università), si immerse nello studio dell'ipotesi del continuo. I tentativi di risolvere questo enigma matematico acuirono i suoi problemi psichiatrici.

Nel frattempo, l'articolo di Godel sulla compatibilita dell'assioma di scelta e dell'ipotesi generalizzata del continuo con gli altri assiomi della teoria degli insiemi apparve nei Proceedings della National Academy of Sciences. L'articolo combinava i due grandi risultati ottenuti da Godel dopo il teorema di incompletezza. Aveva dimostrato che l'assioma di scelta e la generalizzazione di Hausdorff dell'ipotesi cantoriana erano compatibili. Entrambe queste assunzioni enigmatiche riguardanti l'infinito, se considerate vere, non creavano alcuna contraddizione o conflitto con gli altri assiomi della teoria degli insiemi.

La dimostrazione di Godel implica che, se i fondamenti della matematica sono coerenti, allora questi rimangono tali, se si assume la verità di entrambe le asserzioni. La sua dimostrazione non implica che l'ipotesi del continuo (o l'assioma di scelta) è vera. Infatti, il risultato di Godel è a mezza strada dal dimostrare che l'ipotesi del continuo (e l'assioma di scelta) è indipendente dal resto della matematica. Mentre lottava per ottenere un visto per gli Stati Uniti e per sopravvivere in un ambiente divenuto ostile, Godel stava completando la dimostrazione del converso dell'implicazione che stabilisce la compatibilita relativa per dimostrare l'indipendenza.

La dimostrazione di Godel, completata nella notte tra il 14 e il 15 di giugno 1937, implicava che l'ipotesi del continuo poteva funzionare all'interno dell'insieme di assiomi che sono a fondamento della matematica. Se fosse stata dimostrata l'implicazione inversa, l'assioma di scelta e l'ipotesi del continuo sarebbero stati dimostrati completamente indipendenti dalla matematica, nel senso che all'interno del presente sistema non possiamo sapere se Cantor avesse ragione a proposito dei tipi di infinito.

Godel aveva dimostrato che cercare di creare un sistema matematico completo e coerente era un compito impossibile. Le sue idee possono essere enucleate in due enunciati.

I teoremi di indecidibilità

Primo teorema di indecidibilità

Se la teoria assiomatica stabilita è coerente, esistono teoremi che non possono essere né dimostrati né confutati.

Secondo teorema di indecidibilità

Non esiste un procedimento costruttivo che dimostri la coerenza della teoria assiomatica.

La prima affermazione in sostanza significava che qualunque siano gli assiomi utilizzati, ci saranno questioni alle quali la matematica non saprà rispondere e dunque la completezza non potrà mai essere raggiunta. Peggio ancora, la seconda affermazione significava che i matematici non potranno mai essere certi che gli assiomi da loro scelti non conducano a una contraddizione, ossia la coerenza della matematica non può mai essere dimostrata. All'età di soli venticinque anni Godel aveva mostrato che il programma di Hilbert era impossibile.

Anche se il secondo teorema di Godel affermava che era impossibile dimostrare la coerenza degli assiomi, questo non significava necessariamente che fossero incoerenti. Molti matematici erano ancora in cuor loro convinti che la matematica restasse un sapere coerente, anche se con la mente non potevano dimostrarlo.

Per comprendere meglio il teorema di indecidibilità di Godel, la sua origine e le sue implicazioni, si può ricorrere a un analogo paradosso della logica greca antica, che è attribuito a Epimenide di Creta ed è conosciuto come il paradosso del Mentitore.

Epimenide esclamò: «Io sono un mentitore!». Il paradosso sorge quando cerchiamo di stabilire se quest'affermazione è vera o falsa. Vediamo prima cosa succede se assumiamo che l'affermazione è vera. La verità dell'affermazione implica che Epimenide sia un mentitore, ma ciò contrasta con il nostro assunto iniziale che egli ha fatto un'affermazione vera e che dunque non è un mentitore: siamo davanti a un'incongruenza. D'altro canto vediamo cosa succede se assumiamo che l'affermazione sia falsa. La falsità dell'affermazione implica che Epimenide non sia un mentitore, ma noi abbiamo assunto inizialmente che egli abbia fatto un'affermazione falsa e che perciò Epimenide è un mentitore: siamo di fronte a un'altra incongruenza. Sia che assumiamo la verità o la falsità dell'affermazione finiamo per incontrare una contraddizione e perciò l'affermazione non è né vera né falsa, ma viene definita indecidibile.

Godel reinterpretò il paradosso del mentitore introducendovi il concetto di dimostrazione. Ne risultò questo tipo di affermazione:

Questa affermazione non ammette alcuna dimostrazione.

Se l'affermazione fosse falsa, allora essa sarebbe dimostrabile, ma questo contraddice l'affermazione stessa. Perciò per evitare la contraddizione l'affermazione dev'essere vera. Ma, anche se l'affermazione è vera, essa non può essere dimostrata proprio perché l'affermazione (che noi sappiamo ora essere vera) afferma la propria indimostrabilità.

Poiché Godel seppe tradurre l'affermazione di cui sopra in termini matematici, egli potè dimostrare che nella matematica esistevano enunciati che sono veri, ma la cui verità non può mai essere dimostrata, i cosiddetti enunciati indecidibili. Questo era il colpo mortale per il programma di Hilbert.

Sotto diversi aspetti l'opera di Godel è parallela a scoperte analoghe che sono state fatte nella fisica quantistica. Quattro anni prima che Godel pubblicasse la sua opera sull'indecidibilità, il fisico tedesco Werner Heisenberg scoprì il principio di indeterminazione. Proprio come esisteva un limite fondamentale alla possibilità di dimostrare i teoremi da parte dei matematici, Heisenberg mostrò che c'era un limite fondamentale alle proprietà che i fisici potevano misurare. Per esempio, se i fisici vogliono misurare l'esatta posizione di un oggetto, allora possono misurarne la velocità solo in maniera approssimativa. Ciò avviene perché allo scopo di i misurare la posizione dell'oggetto sarebbe necessario illuminarlo con fotoni di luce, ma per determinarne l'esatta posizione i fotoni dovrebbero possedere un'enorme energia. Se però l'oggetto viene bombardato con fotoni ad alta energia, la sua velocità verrà alterata e diventerà intrinsecamente incerta. Pertanto, nell'esigere la conoscenza della posizione di un oggetto, i fisici sono costretti a rinunciare a una conoscenza precisa della sua velocità.

Il principio di indeterminazione di Heisenberg si manifesta soltanto su scala atomica, dove le misure di alta precisione hanno un'importanza fondamentale. Perciò gran parte della fisica può proseguire il proprio cammino senza curarsi che i fisici quantistici si occupino di questioni profonde concernenti i limiti del sapere naturale. Lo stesso è accaduto nel mondo della matematica. Mentre i logici affrontavano un dibattito alquanto esoterico sulla indecidibilità, il resto della comunità matematica proseguiva incurante la propria attività. Benché Godel avesse dimostrato che esistevano alcuni enunciati che non potevano essere dimostrati, ce n'erano moltissimi altri che potevano esserlo e la sua scoperta non invalidava nulla di quanto era stato dimostrato in passato. Inoltre, molti matematici credevano che gli enunciati indecidibili di Godel si sarebbero trovati solo nelle regioni più oscure e marginali della matematica e che perciò poteva accadere che non li si incontrasse mai. Dopo tutto Godel aveva soltanto asserito l'esistenza di simili enunciati, ma non aveva potuto indicarne realmente alcuno. Ma nel 1963 l'incubo teorico di Godel divenne realtà in carne e ossa.

Paul Cohen, un matematico di ventinove anni della Stanford University, sviluppò una tecnica per verificare se una particolare questione fosse o non fosse indecidibile. La tecnica funziona solo in pochissimi casi molto particolari, ma egli fu nondimeno la prima persona a scoprire questioni specifiche che erano davvero indecidibili. Fatta la scoperta, Cohen volò subito a Princeton, con le prove alla mano, per farla verificare dallo stesso Godel. Godel, che era ormai entrato in una fase paranoica della sua vita, aprì leggermente la porta, afferrò i fogli e richiuse l'uscio con violenza. Due giorni dopo Cohen ricevette un invito a prendere il té a casa di Godei, un segnale che il maestro aveva conferito alla dimostrazione il marchio della sua autorevolezza. L'aspetto particolarmente sconvolgente era che alcune di quelle questioni indecidibili erano centrali per la matematica. Per ironia della sorte Cohen dimostrò che una delle questioni che David Hilbert aveva incluso tra i ventitré problemi più importanti della matematica, ossia l'ipotesi del continuo, era indecidibile.

L'opera di Godel, insieme con gli enunciati indecidibili scoperti da Cohen, rappresentava un messaggio inquietante per tutti quei matematici, dilettanti o professionisti, che persistevano nei loro tentativi di dimostrare l'Ultimo Teorema di Fermat: forse quel teorema era in decidibile! E se Pierre de Fermat si fosse sbagliato quando aveva affermato di possedere la dimostrazione? In tal caso, era possibile che l'Ultimo Teorema fosse indecidibile. Dimostrarlo poteva essere assai più che un'impresa difficile; poteva essere un'impresa impossibile. Se l'Ultimo Teorema di Fermat era indecidibile, allora i matematici avevano trascorso secoli alla ricerca di una dimostrazione inesistente.

Curiosamente se l'Ultimo Teorema di Fermat si rivelava indecidibile, allora questo implicava che doveva essere vero. La ragione di questa implicazione è la seguente.

L'Ultimo Teorema afferma che non ci sono soluzioni in numeri interi per l'equazione

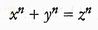per n maggiore di 2.

Se l'Ultimo Teorema fosse falso, allora sarebbe possibile dimostrarlo identificando una soluzione, ossia un controesempio. Perciò, in tal caso, l'Ultimo Teorema sarebbe decidibile. L'essere falso sarebbe contraddittorio con l'essere indecidibile. Invece, se l'Ultimo Teorema fosse vero, non necessariamente esisterebbe un modo altrettanto inequivocabile di dimostrarlo, ossia potrebbe essere indecidibile. In conclusione l'Ultimo Teorema di Fermat potrebbe essere vero, ma potrebbe non esserci il modo di dimostrarlo.

(Tratto da "L'ultimo teorema di Fermat" di Simon Singh - 1999 BUR Saggi e da
"Il mistero dell'alef - Amir D. Aczel - 2000 Il Saggiatore)