Eulero è stato di gran lunga il più generoso fornitore di «denominazioni di origine controllata», offrendo il suo nome a una lista impressionante di formule, teoremi, metodi, criteri, relazioni, equazioni...
Nella geometria, si conoscono il cerchio, la retta e i punti di Eulero relativi ai triangoli, più la relazione di Eulero, che riguardava il cerchio circoscritto a un triangolo. Nella teoria dei numeri, il criterio di Eulero, l'indicatore di Eulero, l'identità di Eulero, la congettura di Eulero... Nella meccanica, gli angoli di Eulero. Nell'analisi, la costante di Eulero. Nella logica, il diagramma di Eulero. Nella teoria dei grafi, di nuovo la relazione di Eulero. Nell'algebra, il metodo di Eulero, relativo alla soluzione delle equazioni di quarto grado. Nel calcolo differenziale, il metodo di Eulero riguardante le equazioni differenziali. Cominciava a girargli la testa, ma era deciso ad arrivare sino in fondo. Equazione di Eulero di una retta sotto forma normale, equazione di Eulero (in collaborazione con Lagrange) nel calcolo delle variazioni. La caratteristica di Eulero (in comproprietà con Jules-Henri Poincaré) riguardante i poliedri, i grafici, le superfici, le varietà differenziali. La trasformazione di Eulero, riguardante le derivate parziali e quella concernente le serie, più il problema dei trentasei ufficiali di Eulero e una quantità di teoremi riguardanti i numeri perfetti, la generalizzazione della formula dei binomi, i grafi connessi, più quello sui poliedri, che è la base della topologia; senza contare una grandinata di formule. Fin qui per i I sostantivi.
Poi ci sono gli aggettivi. Maschile singolare: il ciclo euleriano e il grafo euleriano. Femminile singolare: la funzione euleriana di prima specie, o funzione beta, e quella di seconda specie, funzione gamma, senza dimenticare la catena euleriana di un grafo senza anse. Maschile plurale: i numeri euleriani (diversi dai numeri di Eulero) nel calcolo combinatorio e gli sviluppi euleriani per i seni e le cotangenti di numerosi complessi.
E ciascuno di quei nomi corrispondeva a un metodo originale, a un risultato nuovo, a un concetto inedito!
Eulero, il « re dei numeri amicabili». Mentre i suoi predecessori si erano accontentati,di. scovarne al massimo due o tre coppie, lui ne scoprì oltre sessanta.
Settantacinque volumi! Quarantacinquemila pagine di matematica pensate e scritte da una sola persona! A quelle opere occorreva aggiungere la corrispondenza: ben quattromila lettere.
Leonhard Eulero era nato a Basilea nel 1707, figlio di un pastore calvinista, Paul Eulero. Anche se il giovane Eulero mostrò un talento prodigioso per la matematica, il padre era deciso a fargli studiare teologia perché potesse intraprendere la carriera ecclesiastica. Leonhard obbedì rispettosamente e studiò teologia e lingua ebraica all'Università di Basilea. Fortunatamente per Eulero la città di Basilea era anche la patria dei Bernoulli. I Bernoulli erano una singolare famiglia di matematici che, in sole tre generazioni, aveva prodotto otto menti matematiche di primo livello.
Leonhard Eulero ben presto lasciò la Svizzera per i palazzi di Berlino e San Pietroburgo, dove avrebbe trascorso i suoi anni creativi. All'epoca di Fermat i matematici venivano considerati dilettanti che si trastullavano con i numeri, ma nel Settecento erano trattati come professionisti che risolvevano problemi. La cultura matematica era cambiata drasticamente e ciò si doveva in parte all'opera di Isaac Newton e dei suoi calcoli scientifici. Newton riteneva che i matematici stessero sprecando il proprio tempo stuzzicandosi con assurdi quesiti. Al contrario egli applicava la matematica al mondo fisico e calcolava tutto, dalle orbite dei pianeti alla traiettoria dei proiettili di artiglieria. Alla morte di Newton, nel 1727, l'Europa era passata attraverso la rivoluzione scientifica e nello stesso anno Eulero pubblicò il suo primo scritto. Anche se esso conteneva calcoli matematici eleganti e innovativi, il suo scopo primario era di descrivere la soluzione di un problema tecnico concernente l'alberatura delle navi.
Le potenze europee non erano interessate a una matematica che esplorasse concetti esoterici e astrusi, ma volevano sfruttare la matematica per risolvere problemi pratici e a tal fine entrarono in competizione per ingaggiare le menti migliori. Eulero cominciò la sua carriera presso gli zar, prima di essere invitato all'Accademia di Berlino da Federico il Grande di Prussia. Alla fine tornò in Russia, dove trascorse gli ultimi anni della sua vita durante il regno di Caterina la Grande. Nella sua carriera affrontò moltissimi problemi, che andavano dalla navigazione alle finanze, dall'acustica all'irrigazione. La necessità di risolvere problemi pratici non ottuse l'abilità matematica di Eulero. Al contrario, ogni nuovo compito lo spingeva a creare ingegnosi e innovativi sviluppi matematici.
Uno dei più grandi risultati di Eulero fu lo sviluppo del metodo algoritmico. Lo scopo degli algoritmi di Eulero era di affrontare problemi apparentemente impossibili da risolvere. Uno di questi era quello di prevedere le fasi lunari con la massima accuratezza e spingendosi il più avanti possibile nel futuro: informazione che poteva essere utilizzata per stendere tavole di navigazione molto preziose. Newton aveva già mostrato che è relativamente facile prevedere l'orbita di un corpo intorno a un altro, ma nel caso della luna la situazione non è così semplice. La luna orbita intorno alla terra, ma c'è un terzo còrpo, il sole, che complica enormemente la questione. Mentre la luna e la terra si attraggono reciprocamente, il sole perturba la posizione della terra e in tal modo influisce sull'orbita della luna. Si potevano adoperare equazioni per stabilire l'effetto di ognuno dei i due corpi, ma i matematici del Settecento non sapevano includere il terzo corpo nei loro calcoli. Anche oggi è impossibile prevedere la soluzione esatta del cosiddetto «problema dei tre corpi».
Eulero capì che i naviganti non avevano bisogno di conoscere le fasi lunari con precisione assoluta, ma solo con quell'accuratezza sufficiente a permettere loro di identificare la propria posizione entro un raggio di qualche miglio marino. Di conseguenza sviluppò un metodo per trovare una soluzione imperfetta, ma sufficientemente accurata. Questo metodo, noto come algoritmo, funzionava in modo tale da ottenere in prima istanza un risultato approssimativo, che però poteva essere poi reinserito nell'algoritmo in modo che scaturisse un risultato più preciso. Questo secondo risultato poteva essere di nuovo sottoposto all'algoritmo per generare un altro risultato, ancor più preciso e così via. Dopo cento iterazioni o poco più Eulero fu in grado di fornire una posizione della luna abbastanza precisa per gli scopi della marineria. Consegnò il suo algoritmo all'Ammiragliato britannico e in cambio ricevette un compenso di trecento sterline.
I ponti di Kònigsberg
Eulero si guadagnò la fama di saper risolvere tutti i problemi che gli venivano posti, con un talento che sembrava andare ben oltre il regno della scienza.
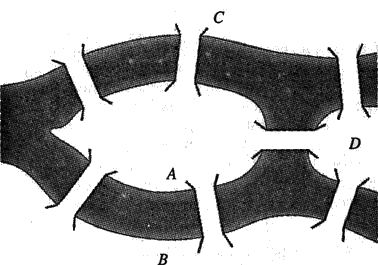Un problema più concreto, che non mancò di attirare il carattere bizzarro di Eulero, riguardava la città prussiana di Kònigsberg, oggi nota con il nome russo di Kaliningrad. La città si erge sulle sponde del fiume Pregel e consiste di quattro quartieri separati, collegati da sette ponti. La figura mostra la mappa della città. Alcuni tra gli abitanti più curiosi si chiesero se fosse possibile immaginare un viaggio passando attraverso tutti i sette ponti senza dover attraversare più di una volta ognuno di essi. I cittadini di Kònigsberg provarono vari percorsi, ma senza riuscire nell'intento. Anche Eulero non potè trovare il percorso richiesto, ma riuscì a spiegare perché un viaggio simile era impossibile.
Eulero cominciò con il tracciare una mappa della città, dalla quale ricavò una rappresentazione semplificata in cui le sezioni di terra venivano ridotte a punti e i ponti venivano sostituiti da linee. Poi argomentò che, in generale, per poter riuscire a effettuare il viaggio ipotizzato (ossia attraversare tutti i ponti una sola volta), un punto dovrebbe essere collegato a un numero pari di linee. Questa deduzione si deve al fatto che nel corso del viaggio, quando un viaggiatore attraversa un'estensione di terra, deve entrarvi da un ponte e uscirne da un altro ponte. Questa regola subisce soltanto due eccezioni: quando un viaggiatore comincia o finisce il viaggio. All'inizio del viaggio il viaggiatore parte da un pezzo di terra e ha bisogno di un solo ponte per uscirne; così pure alla fine del viaggio il viaggiatore arriva in un pezzo di terra e ha bisogno di un solo ponte per entrarvi. Se il viaggio comincia e finisce in località differenti, allora queste due sezioni di terra possono avere un numero dispari di ponti. Ma se il viaggio comincia e finisce nello stesso luogo, allora anche questo punto, come tutti gli altri punti, deve avere un numero pari di ponti.
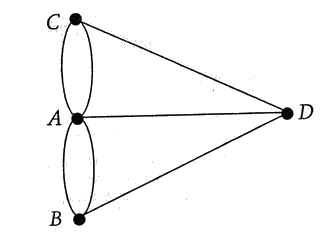Perciò, in generale, Eulero concluse che, per ogni rete di ponti è possibile fare un viaggio completo, attraversando ogni ponte una sola volta, soltanto se tutte le parti di terra hanno un numero pari di ponti o se ci sono esattamente due parti di terra che hanno un numero dispari di ponti. Nel caso di Kònigsberg ci sono in tutto quattro parti di terra e tutte sono collegate a un numero dispari di ponti: tre punti sono collegati a tre linee cioè a tre ponti e uno a cinque linee ossia a cinque ponti. Eulero aveva potuto spiegare perché era impossibile attraversare ogni ponte di Kònigsberg una e una sola volta e inoltre aveva formalizzato una regola che poteva applicarsi a ogni rete di ponti in qualunque città del mondo.
Eulero continuò a creare geniali teorie matematiche fino alla morte, un risultato reso ancor più notevole dal fatto che durante la fase conclusiva della sua carriera rimase completamente cieco. Cominciò a perdere la vista nel 1735, quando l'Accademia di Parigi offrì un premio per la soluzione di un problema di astronomia. Il problema era così arduo che i matematici chiesero all'Accademia qualche mese di tempo per poter formulare la risposta, ma Eulero non ne ebbe bisogno. Si fece prendere dall'ossessione di risolvere il problema, lavorò ininterrottamente per tre giorni e vinse il premio. Tuttavia le condizioni disagiate di lavoro e l'intenso affaticamento costarono a Eulero, che non aveva ancora trent'anni, la perdita della vista dall'occhio destro, come mostrano alcuni suoi ritratti.
Su suggerimento di Jean Le Rond D'Alembert, Eulero venne sostituito da Joseph-Louis Lagrange come matematico alla corte di Federico il Grande, che in seguito dichiarò: «Devo alla vostra cura e ai vostri suggerimenti se ho sostituito un matematico mezzo cieco con un matematico che ha tutti e due gli occhi, cosa che renderà particolarmente soddisfatti gli studiosi di anatomia membri della mia Accademia». Eulero tornò in Russia dove Caterina la Grande accolse benevolmente il suo «ciclope matematico».
La perdita di un occhio non era un handicap grave; «ora avrò minore occasione di distrazione», fu il commento di Eulero. Trent'anni dopo, all'età di sessantanni, la situazione peggiorò considerevolmente, quando una cataratta all'occhio ancora sano lo ridusse alla cecità completa. Egli era però deciso a non smettere di lavorare e cominciò a esercitarsi a scrivere tenendo chiuso l'occhio sinistro, mentre la vista scemava sempre più, per perfezionare la sua tecnica di scrittura prima che sopravvenisse l'oscurità completa. Nel giro di qualche settimana restò cieco. Per un po' i suoi esercizi di scrittura compensarono la sopravvenuta cecità, ma dopo qualche mese la grafia di Eulero divenne illeggibile e il figlio Albert diventò il suo amanuense.
Eulero continuò a produrre matematica nei diciassette anni successivi e fu persine più fecondo che in passato. Il suo intelletto smisurato gli consentiva di sviluppare i concetti senza doverli mettere su carta e la sua memoria fenomenale gli permetteva di usare il cervello come una biblioteca. I colleghi commentarono che l'insorgere della cecità pareva avesse allargato l'orizzonte della sua immaginazione. È degno di nota che il calcolo delle posizioni lunari venne completato da Eulero quando ormai era cieco. Per i regnanti europei quella fu la conquista matematica più importante; si trattava di un problema che aveva confuso i più grandi matematici europei, compreso Newton.
Nel 1776 venne tentata un'operazione per rimuovere la cataratta e per qualche giorno la vista di Eulero sembrò ripristinata. Poi sopravvenne un'infezione ed Eulero sprofondò di nuovo nel buio. Imperterrito continuò a lavorare fino al 18 settembre 1783, quando morì di un colpo apoplettico. Come scrisse il matematico e filosofo Condorcet: «Eulero ha cessato di vivere e di calcolare».
Eulero ed il numero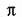 
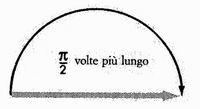
Nel piano, la retta è la distanza più breve tra due punti. Se volete raggiungere il secondo punto descrivendo un percorso circolare, sarà 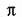/2 volte più lungo!
Si deve ad Eulero la celebre formula
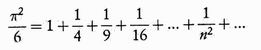
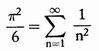
Francoise Viète ne elaborò un'altra davvero sbalorditiva
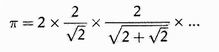
Invece John Wallis trovò che
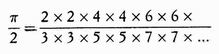
William Brouncker scoprì la seguente meravigliosa espressione
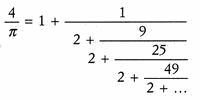
Eulero apportò sostanziali contributi allo studio delle frazioni continue, e scoprì una non meno bella espressione per e, l'altro ben noto numero trascendente:
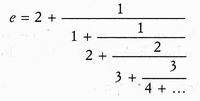
Leibniz costruisce la somma infinita
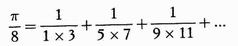
Infine Eulero trova quella che è considerata la più bella e misteriosa formula della matematica, in questa formula si trovano i numeri fondamentali della matematica 1 0 e i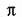
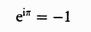
(Tratto da "L'ultimo teorema di Fermat" di Simon Singh - 1999 BUR Saggi)
Leonhard Eulero