Questo libro inizia bruscamente con un elenco di definizioni. La debolezza di questa parte sta nel fatto che alcune di queste non definiscono nulla; infatti non c'è nessun elenco preliminare di elementi indefiniti, in termini dei quali si debbano definire gli altri elementi. Dire che

non significa definire tali entità, poiché una definizione deve essere espressa in termini di concetti che vengono prima e che sono più noti delle cose definite.

La maggior parte delle proposizioni di questo libro sono familiari a chiunque abbia studiato geometria in una scuola superiore. Esse comprendono i teoremi sulla congruenza dei triangoli, sulle costruzioni semplici con riga e compasso, sulle disuguaglianze concernenti gli angoli e i lati di un triangolo, sulle proprietà delle rette parallele e sui parallelogrammi. Il Libro si chiude (Prop. 47 e 48) con la dimostrazione del teorema di Pitagora e del suo reciproco. La dimostrazione del teorema è diversa da quella in cui si applicano proporzioni tra i lati dei triangoli simili formati dall'altezza che viene abbassata sull'ipotenusa.

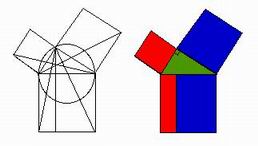Euclide si servì invece di una elegante dimostrazione basata su una figura che viene talvolta descritta come un mulino a vento.

Si ritiene che questa dimostrazione fosse originale di Euclide.

LIBRO II

E' molto breve e tuttavia molto importante: contiene infatti un'algebra geometrica che serve più o meno agli stessi scopi della nostra algebra simbolica.

LIBRO III

Tratta la geometria del cerchio che probabilmente Euclide ha attinto da Ippocrate di Chio. Vengono presentati teoremi sulle posizioni reciproche di una retta e un cerchio e di due cerchi, sulle proprietà delle corde e delle tangenti, sulle relazioni tra angoli e archi e tra angoli al centro e angoli alla circonferenza. La prima proposizione, per esempio, chiede di effettuare la costruzione del centro di un cerchio; l'ultima proposizione contiene il noto teorema secondo il quale, se da un punto esterno a un cerchio si tracciano una tangente e una secante, il quadrato costruito sulla tangente è uguale al rettangolo formato dall'intera secante e dal suo segmento esterno.

LIBRO IV

Le proposizioni trattano come inscrivere e circoscrivere ad un cerchio un triangolo, un quadrato, un pentagono regolare e come costruire un esagono e un pentadecagono inscritti in un cerchio.

LIBRO V

Riguarda la teoria generale delle proporzioni. Alcuni commentatori hanno avanzato l'ipotesi che tutto il libro sarebbe opera di Eudosso, ma ciò sembra poco verosimile. Alcune definizioni (come quella di rapporto) sono così vaghe da risultare inutili. La Definizione 4, però, è essenzialmente l'assioma di Eudosso e Archimede:

Si dice che due grandezze stanno in rapporto l'una con l'altra, quando, se moltiplicate, sono in grado l'una di superare l'altra.

Questo libro tratta di questioni fondamentali. Si apre con proposizioni che sono equivalenti alle proprietà distributive sinistra e destra della moltiplicazione rispetto all'addizione, alla proprietà distributiva sinistra della moltiplicazione rispetto alla sottrazione e alla proprietà associativa della moltiplicazione (ab)c = a(bc). Seguono poi le regole per le espressioni "maggiore di" e "minore di" e le proprietà delle proporzioni.

LIBRO VI

Euclide fa uso della teoria delle proporzioni del Libro precedente per dimostrare teoremi concernenti rapporti e proporzioni relativi a triangoli, parallelogrammi o altri poligoni simili. Notevole è la Proposizione 31, che rappresenta una generalizzazione del teorema di Pitagora:

Nei triangoli rettangoli, la figura costruita sul lato che sottende l'angolo retto è uguale alle figure simili e similmente costruite sui lati che contengono l'angolo retto.

Proclo attribuisce questa generalizzazione allo stesso Euclide. Questo Libro contiene anche (nelle Prop. 28 e 29) una generalizzazione del metodo di applicazione delle aree: infatti ora l'autore era in grado di usare liberamente il concetto di similitudine.

LIBRO VII

Si apre con una serie di definizioni che individuano diversi tipi di numeri: dispari e pari, primi e composti, piani e solidi, infine quelli perfetti. I numeri sono rappresentati da un segmento: così Euclide indicherà un numero AB. Pertanto non usa le espressioni "è un multiplo di" o "è un fattore di", ma si serve rispettivamente delle espressioni "è misurato da" e "misura".

Le prime due proposizioni costituiscono la regola della teoria dei numeri nota come l'"algoritmo di Euclide" per trovare il massimo comune divisore di due numeri. Vi sono poi altre proposizioni sui numeri primi e su come trovare il minimo comune multiplo.

LIBRO VIII

Si apre con una serie di proposizioni concernenti numeri in proporzione continua (progressione geometrica) e quindi si volge a trattare alcune semplici proprietà dei quadrati e dei cubi, terminando con la Proposizione 27:

Numeri solidi simili hanno l'uno con l'altro il rapporto che un numero cubo ha con un numero cubo

Questa affermazione significa semplicemente che, se abbiamo un "numero solido" ma·mb·mc e un "numero solido simile" na·nb·nc, allora il loro rapporto sarà m³ : n³, ossia staranno tra loro come un cubo sta a un cubo.

LIBRO IX

Ultimo dei tre Libri dedicati alla teoria dei numeri, contiene molti teoremi che presentano un interesse particolare. Fra questi il più famoso è la Proposizione 20:

I numeri primi sono più di una qualsiasi assegnata moltitudine di numeri primi.

In altri termini, Euclide presenta qui la ben nota dimostrazione elementare del teorema secondo cui il numero dei numeri primi è infinito. La dimostrazione è indiretta: si mostra infatti che l'ipotesi dell'esistenza di un numero finito porta a una contraddizione. Per esaminare i passaggi di questa dimostrazione si deve accedere al sito Il teorema di Euclide (Dimostrazione) [27].

La Proposizione 35 contiene una formula per la somma di numeri in progressione geometrica espressa in termini eleganti ma insoliti:

Se tanti numeri quanti se ne vuole sono in proporzione continua, e dal secondo e dall'ultimo si sottraggono numeri uguali al primo, allora come l'eccesso del secondo starà al primo, così l'eccesso dell'ultimo starà a tutti quelli che lo precedono.

La successiva, e ultima proposizione, è la ben nota formula per i numeri perfetti:

Se tanti numeri quanti ne vogliamo, a cominciare dall'unità, vengono posti continuamente in proporzione doppia fino a che la somma di tutti i numeri non diventi un numero primo, e se la somma viene moltiplicata per l'ultimo numero, il prodotto sarà un numero perfetto.

Euclide non da alcuna risposta alla domanda inversa, ossia se la sua formula fornisca o no tutti i numeri perfetti. Sappiamo oggi che tutti i numeri perfetti pari sono del tipo euclideo, ma la questione dell'esistenza di numeri perfetti dispari costituisce ancora un problema irrisolto. La ventina di numeri perfetti oggi noti sono tutti pari, ma trarne per induzione la conclusione che debbano essere tutti pari sarebbe azzardato.

LIBRO X

Esso presenta una classificazione sistematica dei segmenti incommensurabili della forma , , , ove a e b, quando sono della stessa dimensione, sono commensurabili. Oggi saremmo inclini a considerare questo Libro come un trattato sui numeri irrazionali del tipo suddetto, ove a e b sono numeri razionali. Ma Euclide considerava questo Libro come facente parte della geometria, piuttosto che dell'aritmetica.

LIBRO XI

Il Libro comprende trentanove proposizioni riguardanti la geometria tridimensionale. Anche qui le definizioni sono facilmente criticabili: Euclide infatti definisce un solido come

ciò che ha lunghezza, larghezza e profondità

e quindi ci dice che

una estremità di un solido è una superficie.

Le ultime quattro definizioni riguardano quattro dei cinque solidi regolari. Non viene incluso il tetraedro, forse per il fatto che era stata precedentemente definita la piramide come

una figura solida, contenuta da piani, che è costruita partendo da un piano e da un qualsiasi punto.

LIBRO XII

Le proposizioni di questo Libro si riferiscono tutte alla misurazione di figure, effettuate con il metodo di esaustione. Il Libro si apre con una dettagliata dimostrazione del teorema secondo cui le aree dei cerchi stanno tra loro come i quadrati costruiti sui diametri. Applicazioni analoghe del tipico metodo della doppia reductio ad absurdum vengono poi usate in relazione alla misurazione dei volumi di piramidi, coni, cilindri e sfere. Archimede attribuiva a Eudosso il merito di avere dato dimostrazioni rigorose di questi teoremi: è pertanto probabile che Euclide abbia attinto da Eudosso gran parte di questo materiale.

LIBRO XIII

L'ultimo Libro è dedicato interamente alle proprietà dei cinque solidi regolari. Questo fatto ha indotto alcuni storici ad affermare che gli Elementi furono composti per celebrare le figure cosmiche o platoniche. Dal momento, però, che gran parte del materiale contenuto nei Libri precedenti non ha nulla a che fare con i poliedri regolari, una tale ipotesi sembra abbastanza gratuita.

L'obiettivo è quello di includere ciascuno dei solidi regolari in una sfera, ossia di trovare il rapporto tra il lato del solido inscritto e il raggio della sfera circoscritta. Tali calcoli vengono attribuiti da alcuni commentatori greci a Teeteto, cui si deve probabilmente gran parte del Libro XIII.

Nella Proposizione 10, Euclide dimostra il noto teorema secondo cui un triangolo i cui lati siano rispettivamente lati di un pentagono, di un esagono e di un decagono equilateri inscritti nel medesimo cerchio, è un triangolo rettangolo. Le Proposizioni dalla 13 alla 17 esprimono il rapporto tra il lato e il diametro per ciascuno dei solidi regolari inscritti, è:

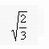per il tetraedro, 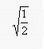per l'ottaedro, 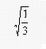per il cubo o l'esaedro, 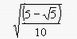per l'icosaedro e 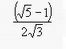per il dodecaedro.

Infine, nell'ultima proposizione, viene dimostrato che non vi possono essere poliedri regolari oltre questi cinque.

Gli Elementi di Euclide non sono solo la maggiore e più antica opera matematica greca che ci sia pervenuta, ma costituiscono anche il più autorevole manuale di matematica di tutti i tempi. L'opera fu composta verso il 300 a.C. e da allora fu copiata ripetutamente. Fu inevitabile che vi si introducessero errori e variazioni; alcuni editori di epoca più tarda (come Teone di Alessandria) cercarono addirittura di perfezionare l'originale. Aggiunte posteriori, che generalmente compaiono sotto forma di scoli, forniscono ulteriori informazioni, spesso di natura storica, e nella maggior parte dei casi sono facilmente distinguibili dall'originale. Copie degli Elementi sono pervenute fino a noi attraverso traduzioni arabe, che in seguito vennero tradotte in latino nel XII secolo. La prima edizione a stampa degli Elementi uscì a Venezia nel 1482 e fu uno dei primi libri stampati.

I POSTULATI SULLE RETTE PARALLELE

In figura la retta r è fissa mentre la retta s può ruotare in senso antiorario attorno al punto P. Indichiamo con Q il punto in cui r ed s si incontrano.

Man mano che s ruota si vede che il punto Q si allontana verso est sulla retta r.

Il punto Q si muove con continuità su r: piccole rotazioni di s determinano piccoli spostamenti di Q (e viceversa). Q assume via via tutte le posizioni possibili su r, "passa" per tutti i punti di r.

Il punto Q dunque si allontana sempre più sulla retta r. Si intuisce però che esiste una (e una sola) situazione in cui sembra proprio che le due rette non si intersechino e quindi Q non esista. In questa situazione le due rette si dicono parallele.

Continuando a ruotare s ci accorgiamo che il punto Q ricompare su r, questa volta però Q è a ovest.

Eccoci arrivati a un punto cruciale. Nella geometria euclidea si assume, assecondando l'intuizione, che per un punto P non appartenente alla retta r passi una e una sola retta s parallela a r (tale cioè che r e s non si incontrino). Tale assunzione non è altro che il quinto postulato di Euclide.

Qui di seguito sono elencati i postulati su cui Euclide (300 avanti Cristo) fondò, negli Elementi, il castello della sua geometria:

Euclide non postula esplicitamente che per due punti passi un'unica retta, ma assume tacitamente che sia così.

Euclide ha già dato la definizione di angolo retto: se una retta r innalzata da un'altra retta s forma con essa angoli adiacenti uguali fra loro, ciascuno dei due angoli è retto. Il postulato P4 è necessario per garantire che gli angoli ottenuti con un'altra costruzione di questo tipo, relativa alle rette r' e s', sono uguali ai precedenti. Il postulato P4 dimostra una notevole raffinatezza logica da parte di Euclide e afferma in sostanza che il piano è uniforme (nel senso che la costruzione predetta fornisce sempre gli stessi angoli, in qualsiasi parte del piano venga eseguita).

In realtà Euclide formulò il quinto postulato in una forma diversa da quella qui riportata ma ad essa del tutto equivalente.

DIMOSTRAZIONE DELL’INFINITA’ DEI NUMERI PRIMI

Un numero maggiore dell'unità si dice primo se ha solo due divisori distinti: 1 e se stesso.

Questa è la legge di rarefazione dei numeri primi. Secondo questa legge si può pensare che i numeri primi siano in numero finito, ma non è così, infatti, Euclide dimostrò che i numeri primi sono infiniti.

Dimostrazione (metodo indiretto):

Si suppone che i numeri primi siano in numero finito.

Esiste allora il numero primo più grande di tutti (MAX).

Se si esegue il prodotto tra MAX e tutti i numeri primi che lo precedono e si aumenta di 1 il risultato, si ottiene un nuovo numero primo N più grande di MAX: infatti dividendo N per ciascun numero primo si ottiene sempre resto 1.

Questa è un’assurdità perché è in contrasto con il fatto che MAX sia il più grande numero primo. Perciò si conclude che i numeri primi sono infiniti.

LE GEOMETRIE NON EUCLIDEE

Sono le geometrie che si fondano sulla negazione del 5° postulato (se una retta che interseca due altre rette forma dalla stessa parte angoli inferiori a due angoli retti, le due rette, se estese indefinitamente, si incontrano da quella parte dove gli angoli sono inferiori a due rette) enunciato negli Elementi di Euclide.

I dettagli di questi due tipi di geometria non-euclidea sono piuttosto complessi, ma in entrambi i casi i concetti fondamentali possono essere compresi per mezzo di semplici modelli.

Geometria iperbolica

La geometria di Bolyai-Lobacevskij, spesso chiamata geometria non-euclidea o iperbolica, ambienta la geometria piana all'interno di una circonferenza, in cui tutte le possibili linee 'rette' sono rappresentate dalle infinite corde.

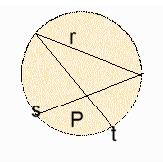
Come si può osservare, tracciato un 'punto' P ed una 'retta' r, si possono trovare due 'rette' s e t, passanti per P e per gli estremi della corda r.

Geometria ellittica

La geometria di Riemann, detta anche geometria ellittica o semplicemente geometria non-euclidea, è costruita sulla superficie di una sfera, in cui tutte le linee rette sono rappresentate dai cerchi massimi.

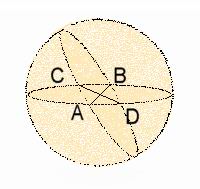
Come si può osservare, fissato un punto di Riemann e una retta di Riemann, ossia una coppia (A, B) di punti diametralmente opposti e una circonferenza massima r, allora ogni altra retta di Riemann passante per (A, B) interseca sempre la circonferenza massima, r, in due punti diametralmente opposti (C, D) ossia in un punto di Riemann.

I DUE TEOREMI DEI TRIANGOLI RETTANGOLI

Molto importanti sono anche i due teoremi sui triangoli rettangoli. Il primo teorema di Euclide enuncia che: “in un triangolo rettangolo ciascun cateto è medio proporzionale tra l'ipotenusa e la proiezione dello stesso cateto sull'ipotenusa”. Con una diversa formulazione si può anche dire che: “in un triangolo rettangolo il quadrato costruito su uno qualsiasi dei cateti è equivalente al rettangolo che ha per dimensioni l'ipotenusa e la proiezione dello stesso cateto sull'ipotenusa” . Il secondo teorema ci dice che: “in un triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale tra le proiezioni dei cateti sull'ipotenusa”. Oppure, usando una diversa versione: “in un triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull'ipotenusa”.

(Tratto da "La sezione aurea" di Mario Livio)

L'enigma di Euclide

Gli elementi di base della geometria euclidea sono il punto, la linea e il piano, nozioni che oggi sono ben note a chiunque abbia seguito un corso di geometria elementare. Euclide formulò anche cinque postulati fondamentali: 1) tracciare una retta fra due punti; 2) prolungare in modo continuo una linea retta; 3) descrivere un cerchio con un centro e un raggio qualsiasi; 4) che tutti gli angoli retti sono uguali fra di loro; 5) che se una linea retta, intersecandone altre due, forma dallo stesso lato angoli interni la cui somma è minore di due retti, se la seconda e la terza retta sono prolungate indefinitamente si incontreranno da quel lato.

Ci sono diverse formulazioni alternative, tutte equivalenti, del quinto postulato. Una, il cosiddetto "assioma di Playfair", dice che per un punto dato si può tracciare una sola parallela a una retta data. Secondo un'altra formulazione, anch'essa equivalente, la somma dei tre angoli interni di un triangolo è uguale, invariabilmente, a due retti (ovvero a 180°); è questa la conseguenza del quinto postulato più facile da analizzare.

Gli specialisti cominciarono a esprimere dubbi sul fatto che il quinto postulato fosse una componente necessaria, o anche solo vera, dell'intera teoria fin dalla pubblicazione degli Elementi, ma il primo ad avanzare critiche veramente serie fu un autore cui dobbiamo gran parte della storia di quest'opera: il filosofo, matematico e storico del V secolo Proclo (410-485 d.C). E grazie a Proclo che sappiamo che Euclide visse durante il regno "di Tolomeo I d'Egitto e che fu lo stesso re a scrivere un libro sul problematico quinto postulato, compresa una prova basata sugli altri quattro. Fu il primo tentativo di cui ci sia giunta notizia di ricondurre il quinto postulato di Euclide ai primi quattro. Nella sua storia dell'opera di Euclide Proclo sostiene, correttamente, che la "dimostrazione" di Tolomeo utilizza l'assunto che per un punto esterno a una retta possa passare una sola parallela a quest'ultima, cioè una proposizione equivalente al quinto postulato! Ma poi cerca di dimostrare anch'egli che il postulato è ridondante, e anche la sua prova è sbagliata.

Il quinto postulato di Euclide, enigma e frustrazione di generazioni di matematici fin da quando il suo creatore lo introdusse, racchiude in sé l'idea che il mondo sia perfettamente piatto: in un mondo piatto le linee rette esistono e possono essere estese all'infinito, restando sempre perfettamente diritte e senza mai piegare nemmeno in misura minima, per quanto vengano prolungate. Immaginiamo una superficie perfettamente piatta: su questa superficie., per un punto esterno a una linea passa una sola parallela a quella linea. Le parallele si estendono all'infinito e non si incontrano mai, restando parallele in eterno. E su questa superficie piatta ogni triangolo ha angoli la cui somma è 180°. Ora immaginiamo che la nostra superficie sia un pezzo (ovviamente piatto) di gomma e che da sotto si alzi una grande sfera che la spinge verso l'alto: la gomma s'incurva intorno alla sfera che sale, finché la superficie diventa essa stessa una specie di pallone. Che ne è di quelle rette che erano parallele? Si piegano; adesso, sulla superficie tondeggiante, si vede chiaramente che vanno a incontrarsi. Su di una sfera non ci sono linee che non si intersechino, e la somma dei tre angoli di un triangolo è maggiore di 180°.

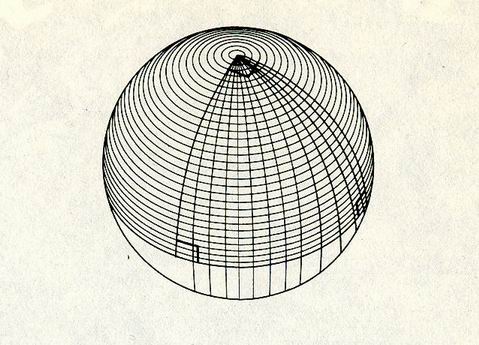
Immaginiamo un triangolo sul globo terrestre, con un vertice al Polo Nord e gli altri due sull'Equatore e consideriamo due meridiani: l'angolo di un meridiano con l'Equatore è retto, 90°; dunque in questo triangolo tracciato sul globo due degli angoli assommano già a 180°, e l'angolo che formano i due meridiani al Polo Nord, dove si incontrano, fa sì che la somma degli angoli di questo triangolo superi i 180°.

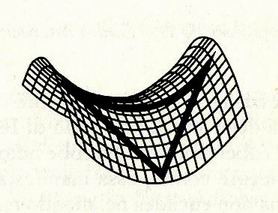
La geometria non euclidea si è sviluppata in una direzione diversa da quella anticipata da Saccheri: la deformazione della nostra superficie piatta originaria da parte di una sfera che spinge da sotto in su. Ma la superficie piatta avrebbe potuto essere deformata anche iperbolicamente anziché sfericamente, cioè stirandola un po' verso l'alto e un po' verso il basso, a sella. In un mondo iperbolico possono esistere, per qualsiasi punto esterno a una retta data, infinite "rette" a essa parallele, e i triangoli sono "magri": la somma dei loro angoli è inferiore a 180°.

Fu in questo strano universo che Saccheri entrò, senza rendersene conto, poco prima di morire. Ma in entrambi i casi, quello iperbolico e quello sferico, la cosa importante è che la superficie piatta venga deformata. Immaginiamo una lastra di marmo piatta sulla quale siano state posate delle sbarre metalliche rettilinee con i vertici che si toccano, formando dei triangoli. Sotto la lastra qualcuno accende un fuoco: il calore del fuoco deforma le sbarre, i triangoli cambiano perché i loro lati s'incurvano, e la somma degli angoli non è più di 180°. Duecento anni dopo Saccheri, Albert Einstein avrebbe fatto proprio questo esempio per spiegare come possa manifestarsi, materialmente, una geometria non euclidea nel mondo reale.

All'inizio dell'Ottocento la matematica era dominata da Karl Friedrich Gauss (1777-1855), un tedesco famoso e geniale che diede alla scienza un contributo prodigioso. Gauss passò decenni a riflettere sul problema del quinto postulato di Euclide, ma pubblicò pochissimo su questo enigma, che aveva consumato così tanto del suo tempo e delle sue energie (pubblicò su molti problemi matematici importanti, ma conosciamo le sue idee sulla geometria soprattutto attraverso le sue lettere); comunque aveva capito chiaramente che la negazione del quinto postulato portava alle geometrie non euclidee.

Mentre era studente alla celebre Università di Gòttingen, Gauss aveva fatto amicizia con un compagno di corso originario dell'Ungheria: Wolfgang (o Farkas) Bolyai (1775-1856). I due dedicarono molto tempo alla ricerca della dimostrazione del quinto postulato di Euclide. Nel 1804 Bolyai si convinse di avere finalmente trovato una prova, la mise per iscritto e mandò il testo, molto breve, al suo ex compagno di studi, che scoprì subito un errore. Bolyai non si lasciò abbattere, proseguì nei propri sforzi e qualche anno dopo spedì a Gauss un'altra dimostrazione, ma anche questa era sbagliata. Wolfgang, che intanto faceva il professore, il drammaturgo, il poeta, il musicista e l'inventore, continuò per tutta la vita le sue ricerche matematiche, nonostante il fallimento dei tentativi di dimostrare un postulato impossibile. Il 15 dicembre 1802 gli nacque un figlio, Janos (Johann) Bolyai (1802-1860); Wolfgang scrisse a Gauss una lettera entusiastica in cui gli parlava della nascita del bambino, "un maschio sano e bellissimo con una buona complessione, capelli e sopracciglia neri e occhi blu che in certi momenti scintillano come due gioielli".

Crescendo, Janos imparò la matematica dal padre, assorbendone l'ossessione per il quinto postulato di Euclide e il desiderio di dimostrare la sua derivazione dagli altri postulati euclidei. Nel 1817 il ragazzo si iscrisse al Regio collegio degli ingegneri dì Vienna, dove dedicò gran parte del suo tempo a inseguire la meta delle passioni paterne: dimostrare il quinto postulato; Wolfgang gli scriveva lettere in cui cercava disperatamente di dissuaderlo dal perdere tempo su un problema impossibile, che aveva consumato tanta parte delle sue energie.

Tuttavia il ragazzo non si lasciò smuovere e continuò a lavorare al problema senza tentennamenti, forse per riscattare in qualche modo i vani sforzi del padre, e nel 1820 raggiunse una stupefacente conclusione: non solo il quinto postulato non era affatto dimostrabile come i normali teoremi di Euclide, ma metterlo da parte significava entrare in un giardino incantato, una nuova scienza assoluta dello spazio, così la chiamò Janos Bolyai, di cui la geometria euclidea era solo un caso particolare. Bolyai partì dalla versione di Playfair del quinto postulato di Euclide {data una linea, per un punto a essa esterno passa una sola parallela), suppose che non fosse vera e concluse che in tal caso o non c'era nessuna parallela alla linea data, o ce n'era più di una. Però una linea retta, secondo un altro postulato di Euclide, era infinita, il che contraddiceva la prima possibilità, lasciando solo la seconda come alternativa praticabile al quinto postulato. Ma se per un punto esterno a una linea data passavano due parallele a quella linea, allora ne passavano infinite.

Le conseguenze di questa conclusione lasciarono stupefatto il giovane Bolyai. La sua nuova geometria si sviluppava senza contraddizioni né ostacoli, come se Dio stesso avesse voluto che la geometria dello spazio seguisse questo nuovo e sorprendente itinerario non euclideo. Soprattutto, entusiasmò Bolyai la scoperta che molte proposizioni erano vere indipendentemente da qualsiasi ipotesi sulle parallele e quindi erano comuni a tutte le geometrie possibili, euclidea e non euclidee; erano queste proposizioni a contenere la natura essenziale dello spazio. Nel 1823 il ragazzo, appena ventunenne, scrisse al padre: "Ho creato dal nulla un universo nuovo e strano".

Il padre fu pronto ad aiutarlo, e inserì il pionieristico lavoro del figlio in appendice a un suo testo matematico, dal titolo abbreviato di Tentamen (Prova), pubblicato nel 1832.

Dopo avere visto il libro dei due Bolyai, Gauss osservò che egli stesso aveva raggiunto conclusioni analoghe nel corso di trentacinque anni di riflessione sul problema del quinto postulato; ma a conclusioni analoghe era arrivato anche un altro matematico: Nikolaj Ivanovic Lobacevskij (1793-1856). Lobacevskij si era laureato nel 1813 all'Università di Kazan, 700 chilometri a est di Mosca, verso gli Urali; in seguito divenne professore e nel 1827 rettore, sempre a Kazan. Oggi è noto come "il Copernico della geometria", dato che la sua creazione, la geometria lobacevskijana, ha rivoluzionato questa scienza eliminando, come aveva fatto, indipendentemente da lui, anche Bolyai, il postulato delle parallele. Nella prima metà dell'Ottocento, quando videro la luce le opere di Bolyai, Lobacevskij e Gauss, alcuni matematici chiamarono "astrale" la nuova geometria non euclidea, intendendola con ciò come "la geometria delle stelle": ma non è ben chiaro come abbiano scelto questo nome.

Nella geometria di Bolyai-Lobacevskij-Gauss la somma degli angoli di un triangolo non è di 180°, e un cerchio non è il solito cerchio della vita (euclidea) di tutti i giorni, poiché il rapporto della sua circonferenza con il diametro non è uguale alla ben nota costante Pi.

Einstein seguì la linea di ragionamento partita dal "pensiero più felice" della sua vita. Creò uno dei suoi famosi esperimenti mentali mentre era ancora all'Ufficio brevetti di Berna immaginando un cerchio che gira nello spazio: il centro del cerchio è immobile, ma la circonferenza ha un rapido movimento circolare. Einstein confrontò quello che accadeva in sistemi di riferimento (la nozione canonica che aveva usato per sviluppare la teoria della relatività speciale) diversi e concluse, usando appunto la relatività speciale, che quando il disco girava il suo contorno si contraeva. Nella parte esterna del cerchio esisteva una forza centrifuga la cui azione era analoga a quella di una forza gravitazionale, ma quella stessa contrazione che agiva sulla circonferenza lasciava intatto il diametro. Perciò, concluse Einstein, e la conclusione sorprese anche lui, il rapporto fra la circonferenza e il diametro non era più Pi; e ne dedusse che in presenza di una forza (o di un campo) gravitazionale la geometria dello spazio non era euclidea.

(Tratto da "L'equazione di Dio" di Amir D. Aczel - 2000 Il Saggiatore)