L'anno in cui Cartesio morì a Stoccolma, il 1650, un bambino di quattro anni di Lipsia, in Germania, guardava le truppe svedesi evacuare la sua città, come stabilito dalla pace di Westfalia, che due anni prima aveva posto fine alla guerra dei Trent'anrti. La Francia e la Svezia, potenze alleate vincitrici del conflitto, dovevano lasciare il suolo tedesco. Ma con la fine dell'occupazione e della guerra, per la Germania ebbe inizio un lungo periodo di declino intellettuale e culturale, conseguenza della devastazione prodotta dagli interminabili anni di combattimenti.
Il bambino, Gottfried Wilhelm Leibniz, era un fanciullo fuori del comune. Già quando aveva quattro anni, coloro che lo conoscevano bene lo trovavano incredibilmente brillante. Suo padre, che era professore all'Università di Lipsia, sapeva che il figlio era un genio, ma purtroppo non ebbe il piacere di assistere ai suoi grandi successi nella vita perché mori all'età di settant'anni, quando il ragazzo ne aveva soltanto sei. Gottfried leggeva i classici greci e latini, che trovava nella biblioteca del padre, e nel giro di pochi anni aveva divorato numerosissimi libri di storia, arte, politica e logica. Ma, pur avendo interessi molto vasti, era particolarmente abile in matematica. E nell'ambito della matematica, il giovane Leibniz aveva un dono molto speciale: sapeva decifrare i codici.
Nella primavera del 1676, quando era a Parigi da più di tre anni, Christiaan Huygens gli parlò dei manoscritti inediti di Cartesio e gli diede il nome di Claude Clerselier. Così il 1° giugno 1676 Leibniz giunse in visita da Clerselier. Gli raccontò la sua storia e lo implorò di permettergli di vedere i manoscritti segreti di Cartesio. Il vecchio acconsentì con riluttanza e Leibniz si sedette e cominciò a lavorare.
La filosofia di Cartesio era un tentativo di fondare la conoscenza umana su una base razionale che aveva il suo modello nella geometria. Cartesio voleva che la gente ragionasse nella vita quotidiana nel modo in cui si ragionava per risolvere un problema di matematica. In questo contesto, il taccuino segreto rappresentava la sua gloria suprema, perché conteneva il livello successivo della geometria, un livello che racchiudeva il mistero dell'universo quale Cartesio lo concepiva.
Leibniz aprì il taccuino segreto di Cartesio, De solidorum elementis, ed esaminò minuziosamente gli scritti che aveva davanti. Non disponeva di molto tempo. C'erano sedici pagine in questo taccuino. O Clerselier gli aveva detto di non volere che lui copiasse il taccuino, oppure gli aveva imposto limitazioni molto rigide nella copiatura.
Leibniz dovette far appello a tutte le capacità matematiche di cui disponeva. Ma aveva gli strumenti necessari per decifrare i codici: era un esperto di combinazioni e di decodifica. Se c'era qualcuno che poteva decifrare il codice di Cartesio, quello era Leibniz. Il filosofo tedesco osservò una pagina del taccuino segreto di Cartesio. Su una facciata c'erano delle figure che Cartesio aveva schizzato molto vicine le une alle altre. Era difficile capire che cosa fossero di preciso. Sull'altra facciata della pagina c'erano formule e simboli che Leibniz non fu in grado di decifrare immediatamente.
Rivolse di nuovo lo sguardo alle figure e allora comprese che cosa dovevano rappresentare: un cubo, un tetraedro (piramide a base triangolare) e un ottaedro (formato da due piramidi a base quadrata unite per le basi).
Il cubo ha sei facce, sapeva Leibniz. Sapeva anche, senza doverli contare perché aveva una mente straordinariamente rapida, che il tetraedro ha sei spigoli e l'ottaedro ha sei vertici. Cartesio stava cercando la bestia dell'Apocalisse. Ciascuna delle tre figure gli forniva un 6, e le tre figure insieme formavano il numero 666. Quindi questa era la ricerca che il grande filosofo francese stava conducendo in segreto: la via rosacrociana al potere occulto. Poi Leibniz voltò la pagina.
Cartesio aveva studiato il cubo, quell'oggetto tridimensionale simmetrico che gli antichi matematici greci avevano invano tentato di duplicare con riga e compasso. Dai suoi contatti con Faulhaber, Cartesio aveva saputo che la piramide era associata con i poteri occulti. Ma voleva saperne di più di questi oggetti misteriosi. Gli Elementi di Euclide, tradotti in latino, gliene fornirono l'opportunità.
Euclide aveva scritto gli Elementi in tredici volumi e vi aveva riportato gli importanti risultati di Pitagora, compreso il suo famoso teorema sui triangoli rettangoli, ricerche sui numeri primi e teoremi di geometria piana, oltre alle proprietà dei triangoli e dei cerchi. Ma nel tredicesimo volume, Euclide aveva dedicato una parte importante del testo ai poliedri regolari, chiamati anche solidi platonici, in omaggio a Plafone che li conosceva.
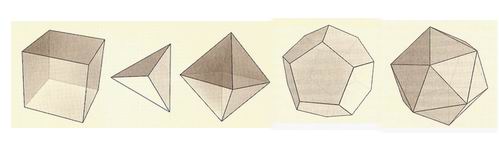
Questi solidi sono detti poliedri regolari perché hanno facce poligonali identiche piane e angoli uguali. Platone sapeva che ci sono soltanto cinque poliedri di questo tipo. Questa circostanza indusse gli antichi greci ad attribuire loro poteri soprannaturali. I poliedri regolari si presentano in natura. Molti cristalli naturali sono poliedri regolari perfetti (o quasi perfetti). Euclide nel tredicesimo volume degli Elementi dimostrò numerosi teoremi sui poliedri regolari inscritti nelle sfere. Per esempio, un cubo può essere inserito esattamente in una sfera, in modo che i suoi otto vertici ne tocchino la superficie interna. Lo stesso si può fare con gli altri poliedri regolari. Questo fatto si rivelò molto importante per le ricerche di Keplero verso la fine del XVI secolo.
Platone identificava i cinque poliedri regolari con i quattro elementi, terra, acqua, aria e fuoco, cui ne andava aggiunto un quinto: l'universo nel suo insieme. Questa concezione esprime l'aura magica che gli antichi matematici e filosofi greci ascrivevano ai concerti e alle entità della matematica e la convinzione che Dio e l'universo fossero matematici.
Cartesio aveva studiato i teoremi euclidei sui poliedri regolari. Ma si sforzava di andare molto oltre Euclide e gli antichi greci. L'uomo che aveva sposato la geometria con l'algebra era alla ricerca di una formula che unificasse tutti i solidi platonici, consentendogli così di estrarne una verità divina relativa alla matematica, e forse alla natura. Una simile conquista matematica suprema avrebbe potuto rendere più efficace e cementare la sua filosofia.
Quando voltò la pagina, Leibniz trovò i rimanenti solidi platonici: il taccuino segreto di Cartesio li conteneva tutti e cinque. L'obiettivo dell'autore, dunque, non era il numero 666. Ma allora che cosa cercava Cartesio nei solidi platonici? Sappiamo che Leibniz copiò il manoscritto in gran fretta. Per una pagina e mezzo di copiatura, non colse il senso generale. Poi d'improvviso comprese tutto: aveva trovato la chiave.
Quasi ottant'anni dopo, nel 1966, un nuovo tentativo di decifrare il taccuino fu compiuto da un gruppo di ricerca che lo analizzò tenendo presente l'informazione tratta da una raccolta delle opere di Cartesio compilata da Charles Adam e Paul Tannery nel 1912. Ma ancora una volta il taccuino rifiutò di restituire i suoi segreti. Il vero significato degli strani simboli, delle sequenze di numeri e dei singolari disegni rimase un enigma.
Nel 1987 Pierre Costabel pubblicò la sua analisi definitiva della copia di Leibniz del taccuino di Cartesio. Questa volta il taccuino svelò i suoi segreti. Costabel aveva studiato attentamente le annotazioni che Leibniz aveva riportato a margine della sua copia del taccuino, e aveva compreso che il filosofo tedesco aveva scoperto la chiave segreta di Cartesio, la quale a sua volta rivelava il vero significato dei suoi scritti. La chiave del mistero era la rego-
la adottata da Cartesio per trattare le sequenze di numeri presenti nel suo taccuino. Questa regola era lo gnomone, un antico termine greco che in origine indicava un'asta usata per proiettare un'ombra sul terreno, la cui lunghezza e direzione era usata per stimare l'ora del giorno. Ma nella matematica greca il termine «gnomone» era venuto a indicare una regola che specificava come si dovevano disporre determinate sequenze di numeri.
Cartesio aveva analizzato i misteriosi solidi di Platone e tra questi oggetti geometrici tridimensionali aveva scoperto la regola che governa la loro struttura. Era il Santo Graal della matematica greca, qualcosa che i greci avevano agognato di possedere. Ma Cartesio non aveva rivelato a nessuno la sua scoperta. Certe conoscenze dovevano essere mantenute segrete. Ma perché tenere così segreto un risultato di geometria?
Giovanni Keplero sapeva che la Terra ruota sul proprio asse e orbita intorno al Sole. Tutte le sue ricerche astronomi-che erano orientate nel senso della concezione copernicana dell'universo, la teoria che anche Cartesio aveva abbracciato, sebbene non in modo pubblico. Keplero, che qualche anno più tardi avrebbe dedotto le leggi del moto planetario - ancora oggi utilizzate in astronomia così come nei voli spaziali -, voleva scoprire la causa della regolarità che osservava nelle orbite dei pianeti del sistema solare. In questo tentativo, nel 1595, quando ancora insegnava in una scuola superiore, ipotizzò che vi fosse una connessione tra la scoperta greca dell'esistenza dei cinque poliedri regolari e le orbite regolari dei sei pianeti noti a quell'epoca (Urano, Nettuno e Plutone dovevano ancora essere scoperti).
Avendo studiato i notevoli teoremi compresi nel tredicesimo libro degli Elementi di Euclide, Keplero sapeva che ciascuno dei cinque poliedri regolari poteva essere inscritto perfettamente in una sfera. Motivato dalla sua ricerca dell'armonia nella struttura del sistema solare, ipotizzò l'esistenza di poliedri regolari celesti, le cui sfere erano inserite l'una nell'altra. Ciascun poliedro regolare era inscritto in una sfera più grande che conteneva tutti i precedenti poliedri e le sfere a essi circoscritte. I cinque solidi platonici risultavano inframmezzati a una sequenza di sfere inserite l'una nell'altra.
Keplero credeva che le orbite della Terra e degli altri cinque pianeti (Mercurio, Venere, Marte, Giove e Saturno) potessero essere concepite come cerchi sulle superfici di queste sfere concentriche, e sapeva dalla geometria greca che i cinque poliedri regolari potevano essere inscritti esattamente in ciascuna di queste sfere. L'astronomo tedesco pubblicò questo modello del sistema solare nel suo libro Mysterium cosmographicum del 1596, e lo considerò uno dei suoi massimi successi, nonché una conferma divina, a mezzo della geometria pura, della teoria copernicana. Ognuna delle sfere conteneva sulla sua superficie l'orbita di un singolo pianeta e racchiudeva al proprio interno un solido regolare. L'ordine dei pianeti e dei solidi era il seguente: Mercurio, l'ottaedro, Venere, l'icosaedro, la Terra, il dodecaedro, Marte, il tetraedro, Giove, il cubo, Saturno.
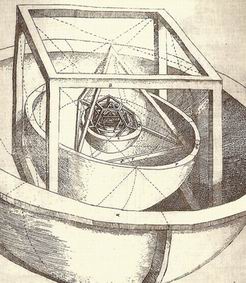
La figura tratta dal Mysterium cosmographicum, mostra il modello cosmologico di Keplero con i cinque solidi platonici inseriti nelle sfere dei pianeti e il Sole al centro.
Alla ricerca di una formula cosmica che governasse i solidi platonici usati da Keplero per spiegare l'universo e dare sostegno alla teoria copernicana, Cartesio cominciò a studiare le proprietà matematiche di questi antichi oggetti geometrici tridimensionali dotati di significato magico. La sua ricerca puramente matematica avrebbe potuto così fornire sostegno teorico alla proibita teoria copernicana dell'universo. Uno dei primi punti trattati nel taccuino segreto di Cartesio era un teorema sulla disposizione dei poliedri regolari all'interno delle sfere, cioè su una proprietà nota agli antichi greci. Ma Cartesio si spingeva molto oltre.
Il filosofo cercava una verità trascendente che descrivesse tutti i poliedri regolari. Più tardi avrebbe scoperto che la formula cui aspirava descriveva non soltanto i cinque poliedri regolari ma qualunque poliedro, regolare o no. Cartesio si proponeva di individuare le proprietà numeriche di questi solidi. Avrebbe poi applicato la sua teoria universale della geometria analitica per ricavarne un legame tra le proprietà algebriche e la struttura geometrica di questi solidi. Ma si rendeva conto che la connessione diretta tra i poliedri regolari della geometria greca antica e il modello di Keplero dell'universo avrebbe potuto far considerare la sua ricerca un argomento a favore della teoria copernicana proibita. Doveva quindi nascondere il suo lavoro per timore dell'Inquisizione.
Leibniz osservò le misteriose sequenze di numeri: 4 6 8 12 20 e 4 8 6 20 12
Qual era il significato di queste sequenze? Leibniz lo individuò.
Cartesio aveva cominciato a contare il numero delle facce dei cinque poliedri regolari, e aveva ottenuto la seguente successione di numeri: 4 (tetraedro), 6 (cubo), 8 (ottaedro), 12 (dodecaedro), 20 (icosaedro)
Poi, per ciascuno dei cinque poliedri, aveva contato il numero dei vertici. Ciò gli aveva fornito, nell'ordine:
4 (tetraedro), 8 (cubo), 6 (ottaedro), 20 (dodecaedro), 12 (icosaedro)
Un semplice sguardo alle figure dei poliedri regolari consente di verificare questi numeri. E in effetti Leibniz comprese che le figure indistinte sull'altra facciata della pagina che stava guardando rappresentavano i cinque poliedri regolari.
Si trattava ora di scoprire come utilizzare le due sequenze. La regola era celata nel modo in cui Cartesio trasformava e mascherava altre sequenze di numeri nel suo testo. Leibniz scoprì lo gnomone e lo annotò sul margine della copia che stava facendo. La regola gli suggerì di disporre le due sequenze di numeri in una tabella, con la seconda sequenza sotto la prima:
4 6 8 12 20
4 8 6 20 12
Ma ecco dove entrava in scena la grande scoperta di Cartesio. Il matematico francese era passato a contare gli spigoli di ciascuno dei cinque poliedri regolari. Aggiungendo questi numeri come terza riga della tabella, si ottiene:
| |
Tetraedro |
Cubo |
Ottaedro |
Dodecaedro |
Icosaedro |
| Facce |
4 |
6 |
8 |
12 |
20 |
| Vertici |
4 |
8 |
6 |
20 |
12 |
| Spigoli |
6 |
12 |
12 |
30 |
30 |
Una volta composta questa tabella, Cartesio aveva fatto la sua scoperta. Aveva notato qualcosa di molto interessante in questi numeri: qualcosa che aveva a che fare con la somma delle prime due righe a confronto con la terza. (Avete visto di che cosa si tratta?)
Quello di cui Cartesio si era accorto è che, per ognuno dei poliedri regolari, la somma del numero delle facce e di quello dei vertici diminuita del numero degli spigoli è pari a due. Ovvero, in una formula:
F+V-S=2
Poi Cartesio aveva scoperto che questa formula valeva per qualunque poliedro, regolare o no. Verifichiamola per una piramide a base quadrata (che non è uno dei cinque poliedri regolari, dal momento che ha una faccia quadrata e quattro triangolari).
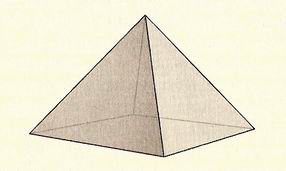
La formula di Cartesio non gli fu mai attribuita. La sua analisi dei corpi tridimensionali avrebbe dato grande impulso alla geometria, se l'avesse pubblicata. Ma poiché temeva l'Inquisizione, questa importante scoperta rimase segreta.
La formula di Cartesio F + V - S = 2 rappresenta il primo invariante topologico che sia stato scoperto. Il fatto che il numero delle facce più il numero dei vertici, meno il numero degli spigoli, sia uguale a 2 è una proprietà dello spazio stesso. Nel dedurre questa formula, Cartesio aveva quindi inaugurato la topologia, che è oggi uno dei più rilevanti settori di ricerca della matematica e ha significative applicazioni in fisica e in altri campi. Ma siccome Cartesio mantenne segreta la sua scoperta, gli viene riconosciuto il merito di avere fondato la geometria analitica, coniugando l'algebra con la geometria, di avere inventato le coordinate cartesiane e di avere compiuto altri importanti progressi in matematica, ma non quello di aver fondato la topologia, lo studio delle proprietà dello spazio. Ad altri sarebbero toccati i riconoscimenti per la fondazione di questa disciplina.
Leonhard Euler (detto Eulero, 1707-1783), nato a Basilea, fu uno dei massimi matematici nel suo secolo. Eulero diede molti contributi alla matematica moderna nelle aree più disparate di questa scienza. Qualche tempo dopo essersi trasferito in Russia per lavorare all'Accademia di San Pietroburgo, scoprì la formula magica che governa la struttura di tutti i solidi tridimensionali: F + V - S = 2, nota come formula di Eulero, anche se, come oggi sappiamo, avrebbe potuto senz'altro essere la formula di Cartesio.
Cartesio non perse soltanto la priorità in una grande scoperta matematica che segnò la fondazione di un'intera area di studio. Nonostante la cura meticolosa con cui per tutta la vita evitò qualsiasi controversia con la Chiesa, tredici anni dopo la sua morte, nel 1663, i suoi scritti furono posti nell'Index Librorum prohibitorum. E nel 1685 Luigi XIV bandì l'insegnamento della filosofia cartesiana in Francia.3 All'epoca di Eulero, nel Settecento, la filosofia di Cartesio quasi scomparve. Nel 1724 i Libraires Associés pubblicarono l'ultima delle edizioni antiche delle opere di Cartesio. Per un secolo in Francia non se ne pubblicò nessuna nuova edizione, e il filosofo fu quasi completamente dimenticato, mentre nuove idee si affacciavano e la filosofia conosceva ulteriori sviluppi. Soltanto nel 1824, esattamente un secolo più tardi, le sue opere furono ristampate, e fu di nuovo riconosciuto come grande filosofo, scienziato e matematico. E l'analisi definitiva di Pierre Costabel, nel 1987, del suo taccuino segreto, ha finalmente restituito a Cartesio il merito di aver fondato lo studio della topologia.
(Tratto da "Il taccuino segreto di Cartesio - Amir D. Aczel - 2005 Mondadori)


