La geometria dell'universo

La geometria dell'universo contribuisce a determinare il suo destino ultimo; i matematici ne distinguono tre possibili varianti. La prima è quella piatta, o euclidea; in un universo euclideo la curvatura è per definizione nulla. La nozione di "curvatura" (per la quale si usa in genere la lettera k) nasce con Gauss; qui partiamo dall'ipotesi che l'universo abbia dovunque una curvatura costante. Se l'universo è piatto si dice che la sua curvatura è k = 0. Gli spazi di curvatura costante non nulla si dividono in due categorie: o la curvatura è positiva, nel qual caso diciamo che k = + 1, o è negativa, e allora scriviamo k = - 1. Uno spazio con curvatura k = + 1 è "chiuso": in due dimensioni è di questo tipo una superficie sferica. Se invece k = - 1 lo spazio è "aperto" e la geometria è iperbolica, come nei modelli di Gauss, Lobacevskij e Bolyai. In due dimensioni, ha curvatura negativa costante la superficie esterna di una pseudosfera.

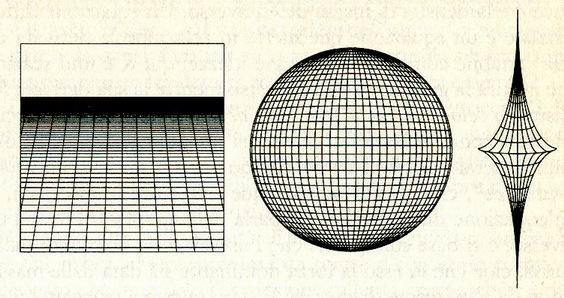
Consideriamo ora le quattro dimensioni dello spazio-tempo; oppure, in modo equivalente, ricostruiamo l'evoluzione nel tempo di un universo tridimensionale usando le tre geometrie a curvatura costante possibili. In questo modo potremo capire perché i cosmologi usano i termini "piatto", "chiuso" e "aperto" per definire universi possibili ognuno dei quali è caratterizzato da una certa forma; per arrivare a questo punto dovremo però tornare all'equazione einsteiniana del campo, che determina appunto la geometria dell'universo.

Senza la costante cosmologica, tale equazione è

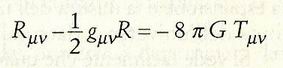
Però se facciamo l'ipotesi che l'universo sia omogeneo, isotropico e a curvatura costante questa formula tensoriale (ricordiamo che le grandezze R_uv, g_uv e T_uv sono tensori, cioè rappresentano configurazioni di elementi e non singoli numeri) si semplifica e diventa un'equazione differenziale scalare (cioè fra grandezze che non sono tensori) scritta nel modo seguente:

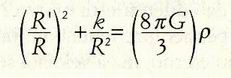
dove p è la densità di massa dell'universo. Un'equazione differenziale è un'equazione che mette in relazione la derivata di una variabile con diverse altre grandezze; qui R è uno scalare che misura la grandezza dell'universo mentre la sua derivata R' misura la velocità a cui la grandezza dell'universo cambia. Perciò questa seconda equazione, che è una semplificazione della formula generale einsteiniana del campo per il caso di un universo "semplice", cioè uniforme ovunque e in tutte le direzioni, è un'equazione differenziale che parla della grandezza R dell'universo, e si basa sull'ipotesi che l'universo sia dominato dalla massa, cioè che in esso la forza dominante sia data dalla massa e non da altre forme di energia. È stato questo a permetterci di rimpiazzare il tensore energia-impulso di Einstein con una grandezza scalare che misura la massa.

Se in questa equazione sostituiamo k con i suoi possibili valori 0, + 1 e - 1 otteniamo, rispettivamente, una densità di massa p dell'universo uguale, maggiore o minore di (R'/R) / (8 Pi G/3). Si tratta di una quantità molto interessante che svolge un ruolo cruciale nei modelli cosmologici. Innanzitutto R, il fattore di scala dell'universo, esprime il raggio di curvatura del cosmo, ammesso che questo sia chiuso e abbia quindi una curvatura (positiva). La quantità R'/R, cioè il rapporto fra la derivata della grandezza del cosmo e questa stessa grandezza, è uguale alla costante di Hubble (indicata in genere con H), che misura il ritmo di espansione dell'universo (cioè la proporzione fra la velocità assoluta di questa espansione e la misura dell'universo). La densità critica dell'universo è data dall'intera quantità (R'/R) / (8 Pi G/3). Si vede facilmente che quando l'universo ha esattamente tale densità, cioè quando p è uguale a questa espressione, la curvatura dev'essere k = 0, corrispondente a un universo piatto. Quando invece p è maggiore, k = + 1: l'universo ha un peso superiore a quello della massa critica, per cui finirà per ricadere su se stesso. Infine, quando p è inferiore alla densità critica la geometria è iperbolica, dato che k = - 1: in questo caso la massa cosmica non è sufficiente e le forze gravitazionali non saranno abbastanza potenti da addensare di nuovo l'universo, che continuerà a espandersi per sempre (anche un universo piatto continuerà a espandersi in eterno, ma a velocità sempre più bassa).

I cosmologi usano un simbolo speciale per il rapporto fra le due densità, la densità di massa reale p dell'universo in un istante dato e la densità critica espressa dalla formula scritta sopra. Questo rapporto fra densità reale e densità critica è detto Omega.

La chiave della geometria dell'universo sta proprio in Omega. Se supponiamo che non esista costante cosmologica, vale quanto segue:

se Omega è uguale a 1 la densità reale è uguale a quella critica e l'universo è piatto, quindi si espanderà per sempre ma la velocità di espansione continuerà a diminuire.

Quando Omega > 1 la densità di massa dell'universo supera la densità critica, che rappresenta un punto d'equilibrio cosmico: in questo caso non solo l'espansione rallenta, ma poiché c'è più massa di quella indispensabile per un semplice rallentamento, verrà un giorno in cui l'universo smetterà di espandersi e comincerà a contrarsi fino all'inevitabile "grande schiacciata", che divorerà tutto. A quel punto forse potrà esserci una rinascita con una nuova grande esplosione, e in questo continuo succedersi di grandi esplosìoni e grandi schiacciate ogni nuovo universo nascerà dalle ceneri del precedente.

Nel caso di Omega < 1 la densità di massa dell'universo è inferiore a quella critica: non c'è massa sufficiente a fermare l'espansione e produrre un collasso, e l'universo continuerà a espandersi per sempre; la sua geometria è iperbolica. Se invece la costante cosmologica non è nulla, l'universo può avere un destino diverso in tutti e tre i casi; questo destino dipenderà dai valori di entrambi i parametri, Omega e la costante cosmologica Lamda.

La geometria dell'universo è determinata dall'evoluzione nel tempo delle tre dimensioni spaziali. Un universo sferico con Omega > 1, che quindi si espanderà e poi comincerà a ricadere su se stesso, avrà un'evoluzione temporale rappresentabile con una cicloide (in questo diagramma quello che in un istante qualsiasi sta per l'universo è un cerchio; sopprimiamo una dimensione spaziale proprio per ottenere un diagramma disegnabile su un foglio).

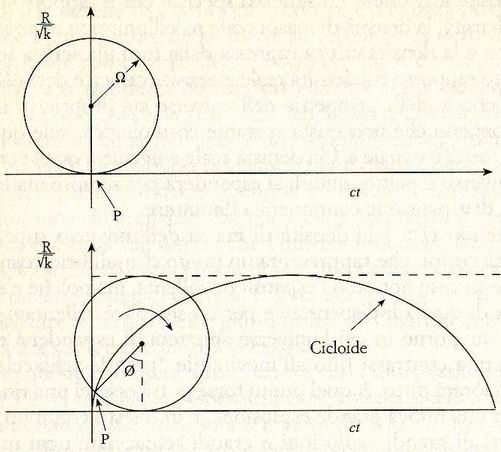
Un universo piatto si espanderà a velocità decrescente, mentre un universo con Omega < 1 si espanderà a velocità crescente.

Ma che cosa succede se nell'universo c'è anche un altro fattore che agisce sulla sua espansione, la sua geometria, il suo destino, se nello spazio esterno c'è un "'energia strana" che non possiamo vedere, avvertire o rilevare ma che opera sul tessuto stesso dello spazio-tempo, facendolo espandere più rapidamente di quanto accadrebbe altrimenti? Se questo fattore esiste, la materia e la sua più importante creatura, la forza gravitazionale, non sono sole. Potrebbe esserci anche qualcosa d'altro. Gli scienziati hanno mostrato una certa tendenza a modificare la definizione di Omega in modo da tener conto di tale possibilità.

Bisognava dare un certo margine di variazione a questo parametro, nel quale sta la chiave dell'universo, per tener conto dell'ignoto; i cosmologi hanno quindi deciso di dividere il valore complessivo di O in due componenti, una da assegnare alla materia e una, in via d'ipotesi, alla costante cosmologica di Einstein. Perciò oggi il parametro che determina la geometria dell'universo è diviso in due: Omega = Omega_M + Omega_Lamda. E se è l'intero O a determinare la geometria dell'universo, il suo destino è determinato quasi esclusivamente dall"'energia strana" Omega_Lamda. Potenzialmente, l'energia della costante cosmologica di Einstein è così grande da poter spingere l'universo a espandersi in eterno quale che sia il valore del termine Omega_M.

Proprio la possibilità di stabilire sia la geometria sia il destino dell'universo stava dietro la fondazione del Supernova Cosmology Project da parte di Saul Perlmutter nel 1988. Gli scienziati che partecipavano al progetto volevano usare le loro osservazioni astronomiche per cercare di stimare i valori dei due parametri Q e per farlo avrebbero studiato le curve luminose delle loro "candele tarate", le supernove di tipo la. Ma i risultati di questo ingegnoso gruppo di astronomi sono andati molto oltre le loro previsioni: dopo anni passati a raccogliere osservazioni ed eseguire calcoli, per i membri del gruppo era assolutamente chiaro che nell'universo operava una forza sconosciuta, di una grandezza mai osservata e mai considerata dalla scienza fino ad allora. Il valore di Omega_M era inferiore a qualsìasi previsione, e le stelle che esplodevano nel cosmo raccontavano una storia strana e incredibile: nell'universo non c'era abbastanza massa da convalidare una qualsiasi teoria che assegnasse proprio alla massa un ruolo determinante, mentre esisteva una, forza invisibile che allontanava tutte le cose le une dalle altre sempre più velocemente. La costante cosmologica di Einstein e il suo simbolo, Omega_Lamda, avevano un'importanza che superava ogni misura.

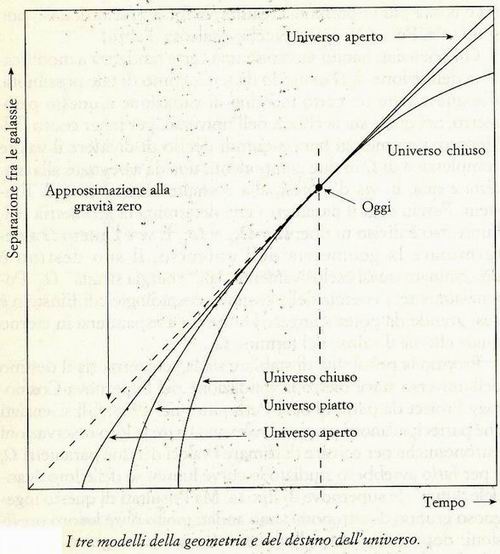
(Tratto da "L'equazione di Dio" di Amir D. Aczel - 2000 Il Saggiatore)