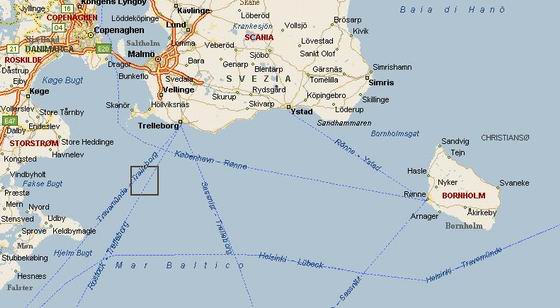
L'isola di Bornholm nel Mar Baltico, appartiene alla Danimarca ed è caratterizzata da bellissime spiagge sconfinate di sabbia bianca a Sud ed impressionanti viste scoscese a Nord. La costa è disseminata di graziosi villaggi di pescatori, mentre all'interno, sono sparse quà e là piccole capanne e belle fattorie. La vita scorre tranquilla, ed oggi è un luogo pacifico ed attraente per quei pochi turisti che passano distrattamente. L'isola però, nasconde segreti meticolosamente celati, e verità impensabili. Il tutto parte dalla vista delle sue chiese.

Nell'isola di Bornholm sono presenti 15 chiese medievali del XII secolo, in pietra molto strane, completamente diverse dalle altre chiese in Danimarca. Tre di queste sono state demolite e ricostruite nel XIX secolo, una è un ammasso di rovine e le altre 11 sono tutt'oggi attive. Dodici di queste chiese sono l'oggetto della nostra attenzione.

Il sistema Bornholm

Le chiese di Bornholm sono incastrate in un intricato schema geometrico, il sistema di Bornholm, che rivela pure e semplici forme di quella che viene definita geometria sacra e che metterà in evidenza rapporti insoliti e inimmaginati di estrema bellezza.

Quattro di queste chiese sono a pianta circolare e in nessun altra parte del mondo, tranne che a Gerusalemme, se ne trova una così alta concentrazione. La pianta circolare e le insolite torri suggeriscono che non fossero pensate esclusivamente come luogo di venerazione, ma anche con uno scopo militare, probabilmente difensivo. La loro pianta mostra tre cerchi orizzontali interattivi. All'interno del simbolismo della geometria sacra, il cerchio è associato al Divino, tre cerchi sono un'espressione dei tre principi divini del cristianesimo: Padre, Figlio, Spirito Santo. Il numero quattro invece è l'espressione della Terra, il mondo materiale, i quattro angoli dell'Universo, i quattro elementi della natura. A Bornholm ci sono quattro chiese circolari in un isola che di per se è già un quadrilatero abbastanza regolare.

C'è un riferimento preciso alle piante di queste chiese, ed è la chiesa di Chateau Pelerin a Athlit in Palestina, costruita dal grande ordine dei monaci combattenti medievali, I Cavalieri Templari.

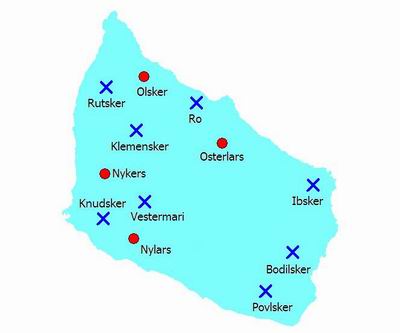
Le quattro chiese a pianta circolare sono : Osterlars, Nylars, Olsker, Nyker.

Le altre chiese sono : Vestermarie, Klemensker, Ro, Bodilsker, Ibsker, Rutsker, Knudsker, Povlsker.

Di seguito diamo le coordinate delle 12 chiese e dei punti più importanti dello schema di Bornholm, così come rilevate dal dipartimento di cartografia danese:

Chiese	Y (Nord=+)	X (Ovest=+)
Osterlars	56.658,790	45.374,730
Nylars	45.803,240	54.738,379
Olsker	63.836,689	55.579,186
Nyker	53.080,615	57.627,126
Vestermarie	49.323,991	54.068,033
Klemensker	57.049,446	55.504,283
Ro	61.006,093	49.529,216
Bodilsker	44.426,870	38.278,728
Ibsker	50.623,036	36.239,257
Rutsker	61.510,228	58.864,891
Knudsker	49.489,060	58.729,969
Povlsker	40.109,421	40.269,569
Punto C	39.444,206	60.223,478
Christianso	73.240,917	31.071,520
Punto P1	49.922,200	50.139,282
Punto P2	49.867,052	51.223,065

Lo schema invisibile

Partendo dalla posizione delle quattro chiese circolari, si ottengono una serie incredibile di figure geometriche di grande precisione:

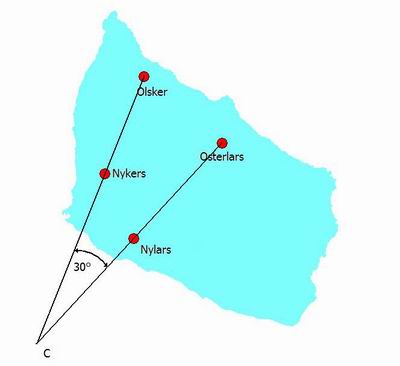
La linea che connette le due chiese più orientali interseca quella che unisce le due occidentali in un punto C, formando un angolo molto vicino a 30°, esattamente di 30.18°, misurato da croce a croce.

Adesso se si prende la chiesa di Osterlars che fra tutte è la più bella ed imponente e la si mette al centro di un cerchio con un raggio pari alla distanza Osterlars-Nylars, abbiamo che le chiese di Rutsker e Bodisker rimangono sulla circonferenza di questo cerchio.

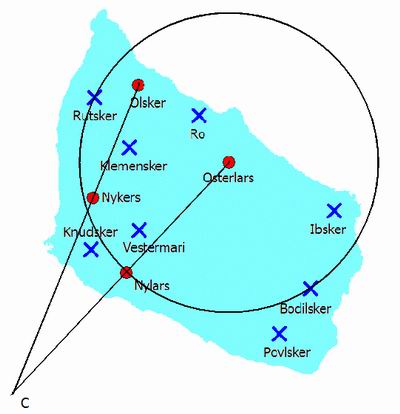
Si può adesso inscrivere un esagono nel cerchio così ottenuto, orientandolo secondo l'asse Osterlars-Nylars, e dalle punte dell'esagono, si ottiene subito la stella di Davide che nella geometria sacra è la forma più importante di tutte.

Da questa nuova figura si nota subito la posizione della chiesa di Olsker che si trova sulla corda dell'esagono, inoltre, la chiesa di Vestermarie è posta sul piccolo triangolo con la punta in Nylars, in maniera tale che la sua distanza da Nylars, sia ad un quarto della distanza tra Nylars e Osterlars.

Inscriviamo adesso un quadrato nel cerchio principale, quindi nel quadrato inscriviamo un cerchio e nel cerchio un ettagono.

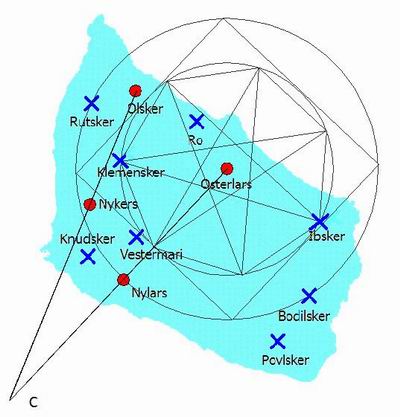
Tutte le figure a tre, quattro e sei lati possono essere facilmente disegnate con l'ausilio di compasso e righello, mentre l'ettagono è impossibile da disegnare con mezzi semplici e lineari. Come si vede due chiese Klemensker e Ibsker cadono su due apici della stella a sette punte. Inoltre il raggio di questo cerchio è uguale alla distanza tra le chiese di Olsker e Nyker. L'ettagono indicato dalla chiesa di Klemensker è un chiaro riferimento al numero 7, tradizionalmente simbolo di saggezza. Sette è un numero razionale, il suo equivalente irrazionale è la radice quadrata di sette, che simboleggia la saggezza spirituale.

La distanza Osterlars-Nylars è la lunghezza di riferimento del sistema di Bornholm. I calcoli rivelano che è in un rapporto molto preciso con la distanza delle altre due chiese circolari Olsker e Nyker. Il rapporto è la radice quadrata di sette.

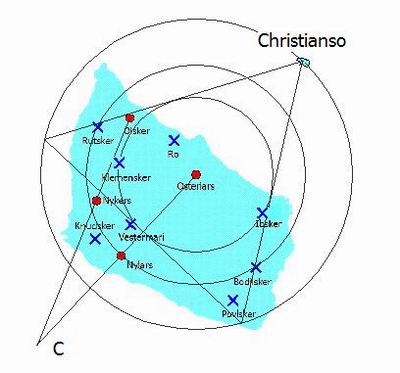
Raddoppiamo il raggio Osterlars-Ibsker e all'interno costruiamo un triangolo equilatero con i lati tangenti il cerchio più piccolo, ogni lato del triangolo è uguale al raggio base Osterlars-Nylars moltiplicato per la radice quadrata di sette. Inoltre una punta del triangolo cade proprio sull'isoletta di Christianso posta a circa 20 Km da Bornholm. Questa isoletta, non più di 700 m sul lato più lungo, si trova proprio sul prolungamento dell'asse centrale del sistema Osterlars-Nylars.

Fin'ora abbiamo visto figure a tre, quattro, sei e sette lati. Nel sistema di Bornholm è ovviamente celata anche la figura a cinque lati, il pentacolo, quello della sezione aurea.

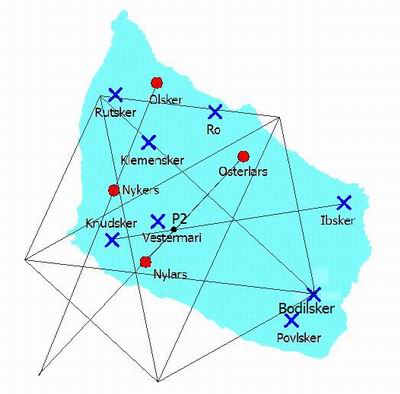
Dividiamo la distanza tra Osterlars e il punto C per la sezione aurea, otteniamo il raggio di un cerchio che produrrà un pentagono orientato sull'asse principale Osterlars-Nylars ed in cui Nylars si trova sull'intersezione dei bracci della stella. Il centro del pentagono è definito dal punto P2, le chiese di Knudsker e Ibsker sono posizionate su una linea passante a conferma del centro. La chiesa di Bodilsker si trova sul vertice del pentagono.

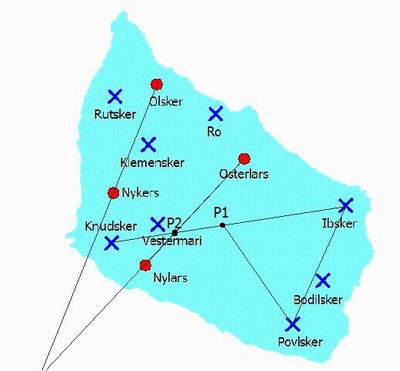
All'inizio di questa ricerca sembrava che Osterlars, la più grande e bella tra le chiese circolari, fosse il centro del mistero. Ma lo schema si è dimostrato più ingegnoso e sottile. Con la scperta del centro del pentagono in P2, e della chiarissima indicazione di P1, il punto più alto dell'isola, si nota che Povlsker è posizionata in maniera tale che la sua distanza da P1 è uguale a quella tra Ibsker e P1 e la metà della distanza tra Ibsker e Knudsker.

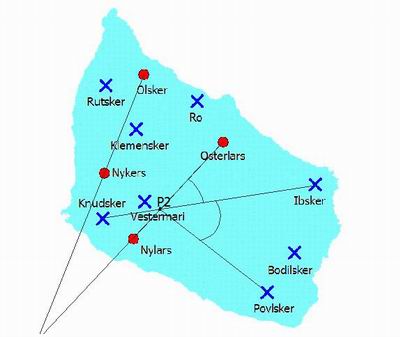
P2 mostra due angoli adiacenti, il primo formato con Osterlars e Ibsker, il secondo tra Ibsker e Povlsker. Il primo è leggermente più grande del secondo. La differenza è 16/9 di un grado.

Dividendo 16/9 per 2 per 2 per 2 e per 2 si ottiene un angolo di 1/9 di grado. Questa è ritenuta un'impresa estremamente brillante in quanto un angolo di tre gradi è il più piccolo che possa essere costruito in gradi interi, e dividere un angolo in tre con regolo e compasso si è dimostrato impossibile, quindi non è possibile costruire un angolo di un solo grado. Il sistema di Bornholm invece dimostra come ottenere un angolo di 1/9 di grado, che moltiplicato per tre e quindi moltiplicato ancora per tre, dà l'impossibile angolo di un grado.

Conclusione

I matematici dell'antichità hanno lottato con tre ingarbugliati problemi:

• La quadratura del cerchio. E' impossibile costruire un quadrato che abbia la stessa area di un determinato cerchio.

• La duplicazione del cubo. E' impossibile costruire un cubo con il volume doppio di quello di un altro determinato cubo.

• La divisione di un angolo in tre. E' impossibile utilizzando solamente regolo e compasso dividere l'angolo in tre parti uguali.