Home page torna al menu quarte classi

APPUNTI DI TERMODINAMICA

La Termodinamica studia il bilancio energetico di un fenomeno. In particolare la Termodinamica chimica studia il bilancio energetico dei fenomeni chimici e cioè la differenza fra il contenuto energetico del sistema chimico prima e dopo la reazione, cioè fra gli stati iniziale e finale, ignorando il particolare percorso che esso effettua (oggetto di studio della cinetica chimica).

Studiare il bilancio energetico di un fenomeno significa individuare e quantificare i modi di trasferimento dell’energia. Il LAVORO è un modo di trasferimento di energia che ha luogo quando le parti di un sistema si muovono sotto l’azione di forze esterne. Il CALORE è un modo di trasferimento di energia che può avvenire quando due sistemi aventi diverse temperature vengono posti in contatto. E’ importante sottolineare che calore e lavoro non vanno intesi come “forme di energia”, ma bensì come modi di trasferimento dell’energia. Infatti, mentre possiamo definire “l’energia di un sistema”, non è altrettanto lecito parlare di “calore di un sistema” o di “lavoro di un sistema”.

Un sistema si definisce aperto se può scambiare energia e materia con l’ambiente circostante. Esso si definisce chiuso se può scambiare solo energia. Si definisce isolato se non può scambiare né energia, né materia.

Per convenzione assegneremo il segno positivo al lavoro (w) che viene compiuto sul sistema e al calore (q) che entra nel sistema, mentre assegneremo il segno negativo al lavoro fatto dal sistema e al calore che esce dal sistema.

Primo principio della termodinamica

Ogni sistema è caratterizzato da una quantità di energia, chiamata ENERGIA INTERNA (U), che rappresenta la somma di tutte le forme di energia possedute dai suoi costituenti (molecole). Per un sistema ideale e chiuso, ad esempio un gas ideale posto in un recipiente chiuso, U dipende solo dalla temperatura. L’energia interna U gode della proprietà che se il sistema subisce una trasformazione passando dallo stato 1, a cui corrisponde il valore U₁, allo stato 2, a cui corrisponde il valore U₂, la sua variazione

DU= U₂- U₁ (1)

è indipendente dal particolare tipo di trasformazione, cioè dal particolare cammino percorso dal sistema per portarsi dallo stato 1 a quello 2. Grandezze di questo tipo vengono chiamate funzioni di stato. Ora, se i soli modi di trasferimento dell’energia in un sistema durante una trasformazione sono il calore e il lavoro si può indicare la variazione di energia interna come

DU= q + w (2)

dove i segni di q e di w sono presi secondo le convenzioni sopra illustrate. Mentre le quantità di calore e di lavoro variano a seconda del particolare cammino che conduce il sistema dallo stato iniziale a quello finale, tuttavia la loro somma algebrica deve corrispondere sempre alla variazione di energia interna tra lo stato iniziale quello finale. La (2) dunque esprime la prima legge della termodinamica. Essa rappresenta un’estensione del principio di conservazione dell’energia alla termodinamica, poiché contempla anche il calore come modo di trasferimento di energia. Perciò essa stabilisce l’impossibilità del moto perpetuo, cioè l’impossibilità di costruire una macchina che produca energia o lavoro utile dal nulla.

trasformazioni reversibili e irreversibili. Processi isotermi e adiabatici

Una trasformazione si dice reversibile se il sistema, passando dallo stato iniziale a quello finale, percorre una serie grandissima di stadi di equilibrio caratterizzati da variazioni piccolissime delle variabili di stato. E’ invece irreversibile se, a causa di variazioni grossolane e repentine delle variabili di stato, il sistema passa dallo stato iniziale a quello finale in condizioni di non equilibrio. E’ importante sottolineare che mentre in una trasformazione reversibile è possibile stabilire e conoscere le relazioni funzionali tra le variabili, e quindi definire delle leggi di stato, in quelle irreversibili ciò non è possibile.

Un processo si definisce isotermo se avviene a temperatura costante. Per realizzare il più da vicino le condizioni isotermiche si suole spesso far avvenire le reazioni in opportuni termostati.

Un processo è adiabatico se avviene senza scambio di calore con l’ambiente. Ci si può avvicinare alle condizioni adiabatiche mediante un accurato isolamento termico, il miglior modo per realizzare il quale consiste nel circondare il sistema con un’intercapedine a vuoto spinto e nel ridurre al minimo le perdite dovute all’irraggiamento con l’uso di pareti molto lucide. Un’applicazione di tali principi si ha nella costruzione dei vasi Dewar.

ENTALPIA

Durante un processo condotto a volume costante non viene eseguito alcun lavoro meccanico. Ne consegue che l’aumento in energia interna eguaglia il calore assorbito a volume costante:

DU= q_v (3)

Consideriamo una trasformazione nella quale l’unica forma di lavoro prodotto dal sistema in una trasformazione reversibile è una espansione contro una pressione P. Se la pressione è mantenuta costante, per esempio in esperienze condotte a pressione atmosferica, e non viene fatto altro lavoro che P×DV, si ha:

DU= U₂- U₁= q + w= q - P×(V₂-V₁) da cui

q =U₂- U₁ + P×(V₂-V₁) e quindi, raggruppando i termini con gli stessi indici,

(U₂+ P×V₂) - (U₁+ P×V₁)= q_p (4)

dove q_p è il calore assorbito a pressione costante. In tal modo viene definita una nuova funzione, l’ ENTALPIA:

H=U +PV (5)

quindi la (4) diventa

DH= H₂-H₁= q_p (6)

L’aumento di entalpia è uguale al calore assorbito a pressione costante quando non viene fatto altro lavoro che P×DV. Poiché U, V e P sono tutte funzioni di stato, anche l’entalpia, che viene definita in termini di queste funzioni, è una funzione solamente dello stato del sistema, cioè indipendente dal cammino secondo il quale tale stato è raggiunto.

CAPACITA’ TERMICA E CALORE SPECIFICO

La capacità termica di una sostanza è il rapporto tra la quantità di calore fornita o ceduta ad essa e la corrispondente variazione di temperatura:

C= Dq/DT

Il calore specifico è la capacità termica dell’unità di massa (mole).

Le capacità termiche a volume costante e rispettivamente a pressione costante sono, per quanto già detto:

C_V= q_V/DT= DU/DT

e

C_p= q_p/DT= DH/DT

Di solito C_p è maggiore di C_v, in quanto a pressione costante una parte del calore assorbito da una sostanza viene impiegato come lavoro di espansione, mentre a volume costante la totalità del calore si traduce in aumento della temperatura (e quindi di energia interna). In particolare, per un gas ideale si può dimostrare che C_p - C_V =nR (7)

dove n è il numero di moli della sostanza e R è la costante universale dei gas.

TERMOCHIMICA - CALORI DI REAZIONE

La termochimica è lo studio degli effetti termici legati ai processi chimici, alla formazione di soluzioni, e a variazioni di stato di aggregazione quali la fusione o l’evaporazione. I processi chimico-fisici si possono classificare in endotermici quando comportano assorbimento di calore, e esotermici quando sono accompagnati da sviluppo di calore.

Come ogni altro trasferimento di calore, il calore di una reazione chimica dipende dalle condizioni del processo dal quale esso è prodotto.

Due particolari condizioni sono importanti perché comportano calori di reazione uguali a variazione di funzioni termodinamiche.

La prima di queste è la condizione di volume costante. Se il volume di un sistema è mantenuto costante, non viene fatto lavoro sul sistema (supponendo che l’unico lavoro possibile nelle date condizioni sperimentali sia quello di volume). L’equazione (2) della prima legge della termodinamica diventa allora:

DU= q_v (8)

Cioè il calore di reazione misurato a volume costante è esattamente uguale alla variazione di energia interna DU del sistema che reagisce. Questa condizione è rispettata nel modo migliore quando si fa avvenire la reazione in una bomba calorimetrica.

L’altra importante condizione particolare è quella a pressione costante. Durante gli esperimenti fatti nelle ordinarie condizioni di laboratorio la pressione è effettivamente costante. Molti calorimetri operano a pressione atmosferica. In questo caso possiamo scrivere, come nell’equazione (6),

DH= q_p (9)

Cioè il calore di reazione misurato a pressione costante è esattamente uguale alla variazione di entalpia del sistema che reagisce.

Per definire il calore di reazione bisogna scrivere esattamente l’equazione chimica per la reazione e inoltre specificare gli stati dei reagenti e dei prodotti, in particolare la temperatura alla quale si è compiuta la misura. Poiché la maggiorparte delle reazioni viene studiata essenzialmente a pressione costante, il calore di reazione é in genere dato dal DH. Ad esempio:

CO₂(1 Atm) + H₂(1 Atm) ® CO(1 Atm) + H₂O(g, 1 Atm),

DH₂₉₈= 41160 (reazione endotermica)

In base alla prima legge, DU e DH per una qualsiasi reazione chimica sono indipendenti dal percorso seguito dal sistema nel passare dai reagenti ai prodotti, e di conseguenza, sono anche indipendenti dalla presenza o meno di reazioni intermedie.

Tale principio, stabilito per la prima volta da G.H.Hess (1840), va sotto il nome di Legge della somma costante dei calori.

Un calore di reazione è quindi calcolabile dai dati riguardanti reazioni chimiche del tutto diverse. Ad esempio:

(1) COCl₂ + H₂S ® 2HCl + COS DH₂₉₈= -78705 Joule

(2) COS + H₂S ® H₂O + CS₂ (l) DH₂₉₈= + 3420 Joule

(3) COCl₂ + 2H₂S ® 2HCl + H₂O + CS₂ (l) DH₂₉₈= -75285 Joule

Entalpie di formazione

Lo stato standard per una sostanza che di solito conviene assumere è lo stato nel quale la sostanza è stabile a 298,15 °K (25°C) e 1 Atm.

Per convenzione le entalpie degli elementi chimici in questo particolare stato standard sono poste uguali a zero.

L’entalpia standard di formazione di un composto, DH^Ä_f, é il DH della reazione con la quale il composto si forma dai suoi elementi, con i reagenti e i prodotti tutti nello stato standard.

Ad esempio, per uno stato standard a 298,15 °K

S + O₂ ® SO₂ DH^Ä_{f 298} = - 296,9 kJ

Molte entalpie standard di formazione sono state ottenute da misure di calori di combustione (reazioni di ossidazione alle quali partecipa l’ossigeno). Infatti, se sono note le entalpie standard di formazione dei prodotti della reazione di combustione di un composto chimico, la sua entalpia standard di formazione si può calcolare dal calore di combustione. Ad esempio,

(1) C₂H₆ + 7/2O₂ ® 2CO₂ + 3H₂O(l) DH^Ä ₂₉₈ = - 1560,1 kJ

(2) C(grafite) + O₂ ® CO₂ DH^Ä_{f 298} = -393,5 kJ

(3) H₂ + 1/2 O₂ ® H₂O(l) DH^Ä_{f 298} = -285,8 kJ

(4) 2C + 3H₂ ® C₂H₆ DH^Ä_{f 298} = -84,3 kJ

Per ottenere come somma la reazione (4) e il relativo valore dell’entalpia standard di formazione, è necessario invertire la reazione (1) di combustione (e quindi anche il segno dell’entalpia standard di combustione), moltiplicare per 2 i coefficienti dell’equazione (2) (e il relativo valore dell’entalpia standard di formazione, essendo le entalpie riferite sempre ad una mole), ed infine moltiplicare per 3 i coefficienti dell’equazione (3) (e il relativo valore dell’entalpia di formazione).

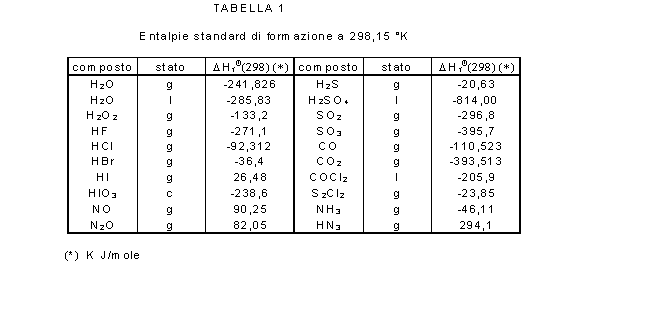
Inoltre per una reazione generica, grazie alla Legge di Hess, la variazione di entalpia standard può essere facilmente ricavata come differenza tra le entalpie standard di formazione dei prodotti e dei reagenti. Nella tabella sottostante sono riportate le entalpie standard di formazione di alcuni composti:

RUDOLF CLAUSIUS (1822-1888)

IL SECONDO PRINCIPIO DELLA TEMODINAMICA

La conversione del calore in lavoro fu oggetto di grande interesse da parte degli ingegneri dal tempo dello sviluppo della macchina a vapore ad opera di James Watt nel 1769. Una tale macchina funziona essenzialmente così: una sorgente di calore (ad es. un fuoco di carbone o di legna) riscalda una sostanza che lavora (ad es. il vapore) e ne provoca l’espansione, attraverso un’opportuna valvola, in un cilindro provvisto di un pistone. L’espansione spinge in avanti il pistone e per mezzo di un adatto accoppiamento si può ricavare lavoro dalla macchina. La sostanza che lavora si raffredda nell’espansione e viene espulsa dal cilindro attraverso una valvola. Un congegno con un volano riporta il pistone alla sua posizione iniziale, pronto per un’altra espansione.

In termini semplici, quindi, una macchina termica riceve calore dalla sorgente termica o serbatoio caldo, ne trasforma una parte in lavoro e cede il rimanente calore allo scarico termico o serbatoio freddo.

Le macchine a vapore subirono un progressivo miglioramento durante la rivoluzione industriale che si ebbe in Inghilterra agli inizi del secolo XIX. Poiché il rapporto tra il lavoro prodotto da una macchina e la quantità di carbone in essa bruciata aumentava con il perfezionarsi delle tecnologie costruttive, non s’intravedeva alcun limite per l’efficienza delle macchine, o rendimento, (e) espressa dal rapporto:

(10)

dove w è il lavoro prodotto dalla macchina (preso col segno negativo, poiché esce dal sistema) e q è il calore fornito (positivo, poiché entra nel sistema).

Fu un ingegnere francese, Sadi Carnot, a dimostrare che il rendimento di una macchina termica ha un limite dipendente unicamente dalla differenza di temperatura dei due serbatoi termici tra i quali lavora la macchina stessa e non dalle sue caratteristiche tecniche, né tanto meno dalla natura del fluido che lavora. Egli illustrò un modello astratto delle caratteristiche fondamentali della macchina termica nella memorabile monografia dal titolo Rifletions sur la Puissance Motrice du Feu.

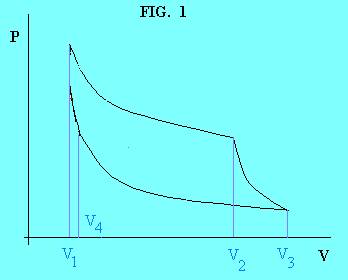
In tale modello la macchina opera tra due temperature T₂ e T₁, con T₂> T₁, ed effettua un ciclo reversibile composto di due trasformazioni isoterme e due trasformazioni adiabatiche (FIG. 1):

serbatoio termico

T₂

q₂

w₃ MACCHINA -w₁

w_{4 __} -w ₂

-q₁

serbatoio termico

T₁

Si può dimostrare che il rendimento assume la forma:

(11)

Combinando la (10) e la (11), si ottiene l’espressione:

(12)

Poiché è concettualmente possibile ridurre un qualunque ciclo reversibile nella somma di un numero grande quanto si vuole di cicli di Carnot operanti tra temperature vicine quanto si vuole, la (12) assume la forma:

(13)

dove dq rappresenta le quantità di calore piccolissime scambiate in ogni ciclo infinitesimo.

Fermiamoci un attimo e facciamo alcune considerazioni:

Affinché una macchina termica possa produrre lavoro deve operare ciclicamente tra due temperature, con espansioni e compressioni cicliche del fluido che lavora. Un altro modo, infatti, di ottenere lavoro può essere quello di far espandere isotermicamente un gas, prelevando calore da un’unica sorgente. Ma ciò non è realistico, poiché comporterebbe l’uso di cilindri di espansione di lunghezza infinita e quindi di nessuna utilità pratica. La macchina quindi deve ritornare ciclicamente al punto di partenza, scaricando una certa aliquota del calore non utilizzato.

Pertanto non è possibile una trasformazione isoterma del calore in lavoro senza una concomitante variazione nel sistema o nell’ambiente.

Provate un po’ a pensare cosa ciò comporterebbe: una nave potrebbe andare avanti senza alcun bisogno di carburante, in quanto il lavoro necessario alla propulsione lo potrebbe ottenere prelevando calore dal mare.

Tale estrazione continua di lavoro dall’ambiente, che l’esperienza indica non essere possibile, prende il nome di moto perpetuo di seconda specie. La produzione di lavoro con un processo ciclico senza alcuna concomitante variazione nell’ambiente (serbatoi termici nel caso del ciclo di Carnot), che è anche impossibile, prende il nome di moto perpetuo di prima specie.

A questo punto possiamo formulare il Secondo Principio della Termodinamica che può essere espresso in vari modi tra loro equivalenti:

Postulato di Kelvin: è impossibile l’esistenza di una macchina a funzionamento ciclico la quale produca come unico effetto l’estrazione di calore da un serbatoio e la produzione di un’uguale quantità di lavoro (moto perpetuo di seconda specie).

Postulato di Clausius: è impossibile l’esistenza di una macchina a funzionamento ciclico la quale produca come unico effetto il passaggio di calore da un corpo più freddo ad uno più caldo.

La formulazione di Kelvin del secondo principio della termodinamica mette in evidenza l’asimmetria della Natura. Infatti, mentre è impossibile convertire il calore totalmente in lavoro, è possibile il contrario. Per esempio gli effetti dell’attrito possono dissipare interamente il lavoro che viene prodotto, come quando una ruota viene frenata. Tutta l’energia trasferita all’ambiente esterno dal motore può venire dissipata in questo modo.

Qui sta dunque la fondamentale asimmetria della Natura: benché il lavoro e il calore siano equivalenti, nel senso che entrambi rappresentano un modo per trasferire energia, essi non sono equivalenti per quanto riguarda la possibilità di scambiarsi l’uno con l’altro. Bisogna tener presente però che l’enunciato di Kelvin stabilisce l’impossibilità di convertire tutto il calore in lavoro, nell’ipotesi che non si verifichino mutamenti nell’ambiente circostante (universo), ma non nega che del calore possa convertirsi completamente in lavoro quando siano contemporaneamente permessi altri mutamenti. Un cannone, ad esempio, può sparare un proiettile: il calore prodotto dalla esplosione della carica è intermante trasformato nel lavoro rappresentato dal lancio del proiettile. Tuttavia questo è un processo istantaneo e lo stato del sistema è completamente differente dopo l’esplosione (ad esempio, il gas che ha spinto il proiettile non viene ricompresso). Ciò vuol dire che si sono verificati mutamenti nell’ambiente esterno al cannone.

NICOLAS LEONARD SADI CARNOT (1796-1832)

L’ENTROPIA

Il Primo Principio, come abbiamo visto, tratta della costanza dell’energia di un sistema non soggetto a influenze esterne; si riferisce cioè ad un sistema isolato (vi ricordo che in termodinamica l’attenzione viene posta su una regione chiamata sistema. Intorno ad esso vi è l’ambiente circostante. I due, insieme, costituiscono l’universo. In pratica, l’universo può essere solo una piccolissima frazione dell’Universo stesso, come l’interno di un recipiente chiuso e termicamente isolato, oppure una certa quantità di acqua mantenuta a temperatura costante).

Supponiamo ora che esistano due stadi dell’universo; ad esempio in uno di essi un blocco di metallo è caldo e l’ambiente circostante è freddo (Stato A), mentre nell’altro è freddo ed in equilibrio termico con l’ambiente (che ora risulta più caldo, avendo assorbito una parte di calore dal metallo) (Stato B) (figura 2).

Stato AStato B

fig. 2

Il Primo Principio afferma che il secondo stato può essere raggiunto a partire dal primo solo se l’energia totale dell’universo è la stessa per entrambi (la qual cosa è verificata, poiché l’universo è isolato). Il Secondo Principio prende in considerazione non l’aspetto che specifica l’energia dell’universo, bensì un altro che ne specifica l’entropia. Definiremo l’entropia in modo tale che se essa è maggiore nello stato B che nello stato A, allora lo stato B può essere raggiunto in modo spontaneo a partire dallo stato A. D’altra parte, anche nel caso in cui l’energia degli stati A e B è la stessa (come in questo caso), se l’entropia dello stato B è minore di quella dello stato A, allora lo stato B non può essere raggiunto in maniera spontanea senza rompere l’isolamento dell’universo, interferendo in qualche modo col nostro universo più grande (causando in questo un mutamento), per portare il sistema dallo stato A allo stato B. Definiamo quindi l’entropia in modo tale che in un universo qualunque essa aumenta quando avviene una trasformazione spontanea, e diminuisce nel caso di una trasformazione che non può verificarsi spontaneamente, ma che deve essere in qualche modo stimolata. Possiamo affermare quindi che: qualunque trasformazione spontanea è accompagnata da un aumento dell’entropia dell’universo. Questo enunciato viene chiamato principio dell’entropia ed è un’altra formulazione del Secondo Principio, equivalente ai postulati di Kelvin e di Clausius. Poichè quindi il principio dell’entropia è equivalente al postulato di Kelvin, l’entropia deve essere definita in modo più dettagliato, come una grandezza che aumenta quando al sistema viene fornito calore, ma rimane invariata quando viene compiuto un lavoro. Inoltre, per la necessaria equivalenza del principio dell’entropia anche col postulato di Clausius, la definizione dell’entropia deve includere la temperatura. In particolare la variazione di entropia che si verifica in un sistema è tanto più piccola quanto più alta è la temperatura alla quale avviene lo scambio di calore. In base a queste considerazioni possiamo matematicamente definire l’entropia nel modo seguente:

Variazione di entropia=(Calore assorbito)/Temperatura

Dove il calore assorbito presenta il segno positivo se esso entra nel sistema, negativo se viene ceduto dal sistema all’ambiente. La Temperatura che compare nella formula è quella alla quale avviene il trasferimento del calore.

Esaminiamo ora nuovamente lo schema della macchina termica da un altro punto di vista:

Fig. 3

Supponiamo di avere una certa quantità di energia che si possa sottrarre ad una sorgente calda, e una macchina per trasformarla in lavoro. Sappiamo che il secondo principio impone di avere anche una sorgente, a temperatura inferiore. Facciamo quindi funzionare la macchina. Possiamo farle produrre una certa quantità di lavoro e pagare la tassa che dobbiamo alla Natura, scaricando una parte di energia sotto forma di calore nella sorgente a bassa temperatura. Questa frazione di energia non è quindi più disponibile per compiere un lavoro (a meno di non disporre di un’altra sorgente a temperatura ancora più bassa). Quindi, in un certo senso, l’energia immagazzinata a temperatura alta è di “qualità” migliore: l’energia di alta qualità è utilizzabile per compiere un lavoro; l’energia di “bassa”qualità, l’energia degradata, è utilizzabile in minor misura.

Un altro modo di considerare la qualità dell’energia è di pensare in termini di entropia. Supponiamo di assorbire una certa quantità di energia sotto forma di calore dalla sorgente a temperatura più alta e facciamo in modo che questa volta venga direttamente ceduta alla sorgente a temperatura inferiore. L’entropia dell’universo diminuisce di una quantità pari a (calore assorbito)/Temperatura_calda, ma aumenta anche di una quantità pari a (calore assorbito)/Temperatura_fredda. La somma dei due contributi produce una variazione globale di entropia positiva, poiché la temperatura della prima sorgente è maggiore di quella della seconda. L’energia dell’universo resta quindi meno utilizzabile per compiere lavoro (infatti quando l’energia è immagazzinata a una temperatura inferiore si rende necessaria la presenza di una sorgente a temperatura ancora più bassa se vogliamo convertire questa energia in lavoro). Possiamo dunque dire che tale energia è di qualità inferiore e che l’entropia ad essa associata è aumentata. L’entropia, quindi, identifica il modo con cui l’energia si trova immagazzinata. Pertanto possiamo affermare che la direzione spontanea di una trasformazione, cioè quella che corrisponde ad un aumento di entropia, è quella che produce una diminuzione della qualità dell’energia.

Quanto visto riguardo all’energia e all’entropia è di grande importanza dal punto di vista pratico. Il Primo Principio stabilisce che la quantità di energia di un universo è costante. Perciò quando bruciamo combustibili fossili come carbone, petrolio e nuclei atomici non diminuiamo la riserva di energia. Da questo punto di vista non potrà mai esserci una crisi energetica, poiché la riserva globale di energia rimarrà sempre la stessa. Tuttavia, tutte le volte che bruciamo un blocco di carbone o una goccia di petrolio, e ogniqualvolta un nucleo si disintegra, aumenta l’entropia del mondo (dato che tutti questi processi sono spontanei). In altre parole, qualunque azione degrada la qualità dell’energia dell’universo. Non siamo perciò nel mezzo di una crisi energetica: siamo sulla soglia di una crisi di entropia, perché la civiltà moderna sta progressivamente deteriorando le riserve di energia dell’universo. Ciò che dobbiamo fare non è conservare l’energia, poiché la Natura lo fa automaticamente, ma amministrarne con parsimonia la qualità. La conservazione della qualità dell’energia rappresenta l’essenza del problema e il nostro compito per il futuro.

LUDWIG BOLTZMANN all’età di 60 anni (1844-1906)

Ritorna all’inizio della pagina

“Con un po’ di pazienza, un po’ di comprensione, un po’ di gioia e un po’ di umiltà, non avete idea di quanto potreste trovarvi bene in questo nostro pianeta Terra”

Gilbert Chesterton, scrittore inglese