A FURIA DI ANDARE
A FONDO DELLE COSE, UNO CI RIMANE SOTTO(Jean Cocteau)
CONSIGLI UTILI PER LA
RISOLUZIONE DEGLI ESERCIZI
I
consigli che seguono derivano dalla mia
esperienza personale e quindi sono limitati, incompleti e forse inutili. Spero comunque
che possano in qualche modo aiutarvi.
Vi è mai
capitato di leggere una sola volta una cosa alla quale eravate molto
interessati e di averla memorizzata e capita immediatamente? (ad esempio i
risultati delle partite del campionato di calcio (non è un sale!), le modalità
per partecipare ad un concorso di bellezza, le istruzioni per l’uso del
cellulare, ecc.). La molla di questo rapido apprendimento sono il vostro
interesse per l’oggetto della lettura e l’estrema concentrazione su ogni parola
del testo.
Bene, se
leggeste allo stesso modo il testo di una traccia di un esercizio di chimica (o
di qualunque altra materia) sareste ad un ottimo punto sulla via della sua
risoluzione. Poiché, però, trovare un alunno appassionato di chimica è più
difficile che far reagire un atomo di elio (bella questa!), le tracce degli
esercizi vengono lette svogliatamente, o, peggio ancora, con l’intima,
irriducibile convinzione che voi non sarete mai capaci di risolverli. Questo
attacco porta a un vicolo cieco. Allora:
1.
Disponetevi in modo
positivo davanti al problema, dicendo con convinzione a voi stessi che siete in
grado di risolverlo. (Questo atteggiamento sarà tanto più efficace, quanto più
avrete studiato. Ricordatevi che la coscienza di avere svolto al massimo delle
nostre capacità un compito che ci viene assegnato (lo studio, in questo caso)
ci dà la pace del cuore e una carica potente).
2.
Poiché non è la passione
che vi guida alla lettura della traccia dell’esercizio, ma la costrizione,
supplite all’inevitabile scarsa concentrazione leggendo molte volte la
traccia. In questo modo vi accorgerete di particolari che vi erano
sfuggiti, di dati numerici ai quali inizialmente non avevate dato importanza,
focalizzerete bene la o le domande dell’esercizio, vi renderete conto che
alcuni dati sono espressi in unità di misura che necessariamente dovranno
essere cambiate in altre attraverso fattori di conversione, ecc . Terminate la
lettura della traccia solo quando “siete entrati nel problema”, cioè quando in
modo del tutto naturale vi sorprendete attori del vostro film mentale nel quale
state operando in un laboratorio di chimica ed eseguendo le operazioni indicate
nella traccia.
Ho
sempre tratto molti vantaggi dalla lettura di “Topolino”, poiché ciò mi ha
permesso di esprimere in vignette un concetto mentale, ed in questo modo ho
tradotto in figure e simboli gli oggetti e le operazioni del film virtuale,
facendomelo sembrare realistico. Allora:
3.
Disegnate, come
meglio sapete o potete, gli oggetti e le operazioni indicate nell’esercizio. Ad
esempio:
……a
250 ml di una soluzione al 20% m/V di solfato di sodio si aggiunge acqua fino
ad ottenere una soluzione al 5% m/V…….
In questo modo
possono venirvi ottime idee per la risoluzione dell’esercizio.
4.
In base all’argomento
che tratta l’esercizio o alle grandezze incognite delle quali l’esercizio vuole
il valore, scrivete, anche senza nessuna strategia in mente, tutte le formule
che possono essere potenzialmente utili e manipolabili ai fini della soluzione
(ricordate la frase famosa: “gettate le formule sul foglio!”).
5.
Cominciate a
elaborare una strategia, senza affrontare nessun calcolo o usare formule, ma
semplicemente formulando passaggi logici, possibilmente con l’uso di diagrammi
di flusso, in modo da “sminuzzare” il problema.
Riprendendo l’esempio precedente, possiamo scrivere, se il problema
chiede il volume di acqua da aggiungere:
se si diluisce la soluzione
la
quantità di sale inizialmente presente deve essere sempre la stessa
allora
si calcola prima di tutto la massa di sale presente nella soluzione iniziale
Poiché, aggiungendo
l’acqua, tale massa deve rimanere costante, calcolo il volume totale nel quale
essa
è presente in ragione del il 5%
Ma
il problema vuole il volume di acqua da aggiungere:
allora sottrarrò dal volume totale calcolato, quello della soluzione
iniziale
6.
Passate
dalla strategia ai calcoli, utilizzando le formule opportune per il calcolo
delle grandezze fisiche o chimiche da voi individuate nella sequenza dei
passaggi logici. Dovreste trovare le formule utili a tale scopo tra quelle da
voi scritte inizialmente, in base alle leggi o alle definizioni che secondo
voi, dopo la lettura attenta della traccia, potrebbero essere essenziali alla
risoluzione del problema.
6.
Un utilissimo modo
per controllare la correttezza dei passaggi algebrici necessari per isolare le grandezze
incognite è quello di effettuare in ogni calcolo l’analisi dimensionale.
Essa consiste nello scrivere e mantenere nei calcoli, accanto ad ogni dato
numerico, le corrispondenti unità di misura. Le operazioni fatte sui dati
numerici, pertanto, saranno le stesse per le unità di misura. Alla fine l’unità
di misura che accompagnerà il dato numerico risultante dovrà essere coerente
con la grandezza che è stata calcolata. Facciamo un esempio banale: se dobbiamo
calcolare la massa del sale in 250 ml di soluzione al 20% m/V, impostiamo la
proporzione:
notiamo
subito l’incongruenza del risultato, dall’unità
di misura ottenuto. Accortici
dell’errore, rivediamol’impostazione e i calcoli,
evitando così l’errore grossolano. Se non avessimo fatto l’analisi
dimensionale, non ci
saremmo probabilmente accorti di tale errore.
I calcoli ormai sono effettuati (purtroppo) solo con le calcolatrici. Sebbene l’uso di queste abbia liberato (ancora: purtroppo) voi ragazzi dall’effettuare i calcoli a mano, con la conseguente possibilità di fare errori, è necessario altresì ricordare che gli errori di battitura delle cifre o gli errori di impostazione delle operazioni aritmetiche sulla calcolatrice sono molto più frequenti di quanto non si creda. Non cessa mai di meravigliarmi il fatto che quando viene svolto un esercizio in classe e chiedo ai ragazzi di usare le loro calcolatrici per effettuare gli opportuni calcoli, mi vengono forniti solitamente quattro o cinque risultati differenti (e in qualche caso nessuno di questi è giusto!). Allora:
7.
Per controllare
l’esattezza dei calcoli effettuati con la calcolatrice è importante utilizzare
il cosiddetto calcolo rapido. Tale tecnica consiste nel trasformare in notazione
scientifica tutti i numeri da introdurre una formula, trasformandoli cioè
in numeri decimali, con una sola cifra prima della virgola, moltiplicati per una corretta potenza di dieci. Esempio:
a) 1345 =1,345·103; ancora:
b) 0,000432=4,32·10-4. Come si vede, l’esponente della potenza in base 10, nel
caso di numeri > 1
(come
nell’esempio a), è positivo ed è uguale al numero dei “posti” che
dobbiamo contare, a partire dalla cifra a destra, per arrivare alla virgola. Se
il numero è < 1 (esempio b), l’esponente è negativo ed è uguale al
numero totale di zeri che precedono la prima cifra diversa da 0. fatto ciò,
si procede alle operazioni con le potenze in base 10 per ottenere l’ordine di grandezza
del risultato. Esempio:
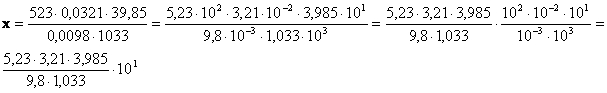
la
potenza 101 è l’ordine di grandezza cercato della grandezza x. Le operazioni alla sinistra dell’ordine di grandezza si
svolgono rapidamente approssimando i numeri ( che ormai sono compressi
nell’intervallo 1-9) all’intero più vicino. Nel nostro caso:
Il numero che dovremmo vedere sul display
della calcolatrice dovrebbe essere vicino al valore 6,7·101 = 67. Il numero esatto, ottenuto con la
calcolatrice è 66,085, molto vicino a quello approssimato. Se avessimo fatto errori di battitura, ad esempio dimenticando una
cifra, aggiungendo o dimenticando uno o più zeri, battendo il tasto x al posto
di 
,ecc., avremmo fatto un errore che senza dubbio si sarebbe
propagato ai calcoli successivi, facendoci sbagliare tutto. Se invece si fa
precedere il calcolo rapido ogni volta alle operazioni sulla calcolatrice, si
ha un controllo e un riscontro immediato della esattezza delle operazioni
effettuate. Molto spesso mi viene detto che il calcolo rapido non è affatto
“rapido” e che quindi farebbe perdere troppo tempo. E’ solo questione di
pratica e si diventa padroni di questa tecnica in men
che non si dica. E’ utilissimo anche nella vita di tutti i giorni e consente un
allenamento costante del cervello.
