[sģ]
Il moto
(rettilineo,
curvilinio e armonico)
181. La tabella sotto esprime le coordinate di una sferetta lanciata orizzontalmente in funzione del tempo rispetto a un sistema cartesiano con l'asse x orizzontale e l'asse y verticale orientato verso il basso. Determinare la velocitą di lancio della sferetta e l'equazione della traiettoria.
| t (s) | 0 | 1 | 2 | 3 | 4 |
| x (m) | 0 | 0,7 | 1,4 | 2,1 | 2,8 |
| y (m) | 0 | 4,9 | 19,6 | 44,1 | 78,4 |
[0,7 m/s; y = 10 x2]
182. ipetere l'esercizio precedente per una sferetta le cui coordinate sono espresse in funzione del tempo secondo la tabella in basso.
| t (s) | 0 | 1 | 2 | 3 | 4 |
| x (m) | 0 | 5 | 10 | 15 | 20 |
| y (m) | 0 | 4,9 | 19,6 | 44,1 | 78,4 |
[5m/s; y= 4,9 x2/25]
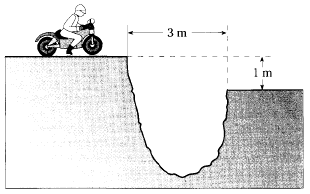
183. Un motociclista che
viaggia alla velocitą di 54 km/h incontra improvvisamente
un'interruzione stradale dovuta a un fossato. La strada continua
al di lą del fossato, a distanza orizzontale di 3 m con un
dislivello di 1 m. Stabilire se il motociclista supera il fossato
oppure no.

[sģ]
184. Un motociclista,
viaggiando alla velocitą v0, incontra improvvisamente
un'interruzione stradale dovuta a un fossato. La strada continua
al di lą del fossato a distanza orizzontale L con un dislivello
h. Determinare la condizione cui devono soddisfare i parametri v0,
L e h affinchč il motociclista superi il fossato.
[ g L2 /2 v02 £ h]
185. Un punto materiale si
muove di moto armonico con equazione oraria x = 50 cos pt/32. Calcolare il periodo, la velocitą
e l'accelerazione in funzione del tempo.
[64; v=-25/16p sen pt/32;
a=-25/512p2 cos pt/32]
186. Un punto materiale si
muove di moto circolare uniforme con periodo 48 s sopra una
circonferenza di raggio 40 cm. Calcolare l'equazione oraria dei
due moti armonici, proiezioni del moto circolare uniforme su due
diametri perpendicolari,
nell'ipotesi che il punto si trovi per t = 0 a un estremo di uno
dei due diametri.
[x = 40 cos pt/24; y=40 sen pt/24 ]
187. n punto materiale si muove
di moto circolare uniforme con velocitą 100 p cm/s sopra una circonferenza di raggio
25 cm. Calcolare il periodo, l'equazione oraria dei due moti
armonici, proiezioni del moto circolare uniforme su due diametri
perpendicolari, nell'ipotesi che il punto per t = 0 si trovi a un
estremo di uno dei due diametri.
[0,5s; x =25 cos 4pt; y =25 sen
4pt]
188. Le proiezioni di un moto
circolare uniforme sopra due diametri ortogonali si muovono di
moto armonico con equazioni orarie:
x = 25 cos pt/8 e y = 25 sen p t/8
con x e y espressi in cm.
Determinare i valori della velocitą e dell'accelerazione dopo 8
s e l'accelerazione centripeta del moto circolare uniforme.
[0; - 9,82 cm/s; 3,86 cm/s2; 0; 3,86 cm/s2]