Cascade Stages  

A common-cathode triode stage exibits an harmonic spectrum decreasing (in a monotonic way)              with the frequency and the contribution furnished from even harmonics (particularly the second one) is preponderant. A similar pentode stage presents a wider spectrum and therefore a general          increment in the THD values and a greater contribution furnished from odd harmonics.  These two different behaviours between triodes and pentodes in the common-cathode configuration  could be easily justified by observing that the mutual dynamic characteristic (the true entity that     characterizes in an unambiguous manner the non linear behaviour of any amplifier stage), is easily         referable to  2nd and 3rd geometric curve for triodes and pentodes rispectively as the Fig. 1, extracted      from Radiotron Designer’s Handbook, it puts clearly in evidence [2]. This different behaviour from the two classes of thermionic devices more used in the amplification technique surely plays a role in favor of  triodes since even harmonics are simpler to reduce. In fact, when correctly implemented, triode stages     with HCT  can easily exhibit very low values in the T.H.D. if phase distortions are negligible.

 

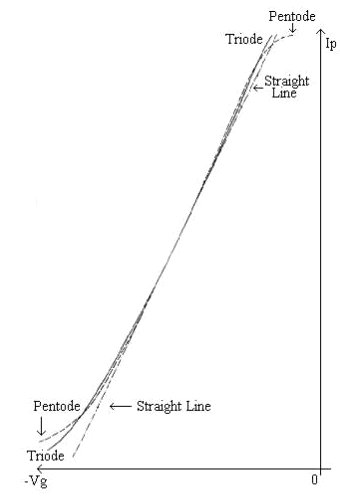
Fig. 1

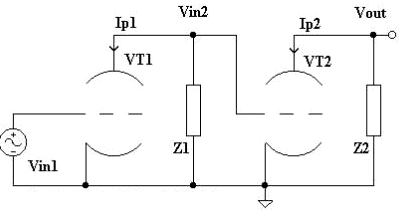
Fig. 2

In the signal domain  a triodes cascade stage  is reproduced in Fig.2.This schematic can represent  most of the circuits that you can meet really, Figg. 3-6.  

 

Fig. 3
 

 

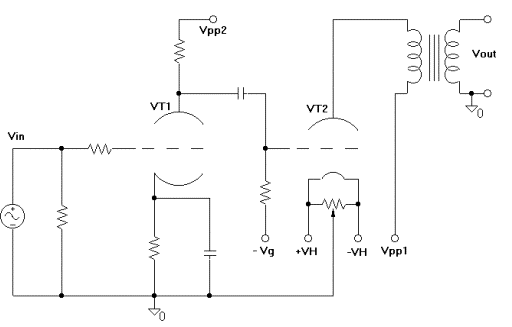
Fig. 4
 


Clearly, other variants exist with pentodes and/or buffers that can be represented with the scheme of  Fig. 2. These circuits in their disarming semplicity have a good fitting with the HCT, further  they result easy to build and above all are good sounding. The variants of this schemes in wich the coupling between the stages happens with an iron (inductor or transformer), Fig. 5-6, are more immediate and easy to manipulate since it’s often sufficient to alter the resistor in the grid’s output tube to put the HCT in the best condition of operation without altering dangerously the bias of the drive stage. On the power amplification side, the only constraint is, in my opinion, the accurate choice of the tube for the drive stage. The main characteristics

 

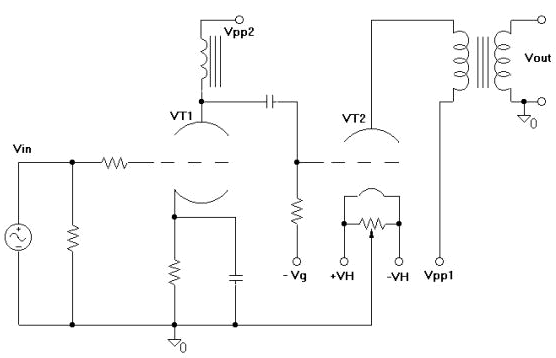
Fig. 5
 

 

 

 

 

 

 

 

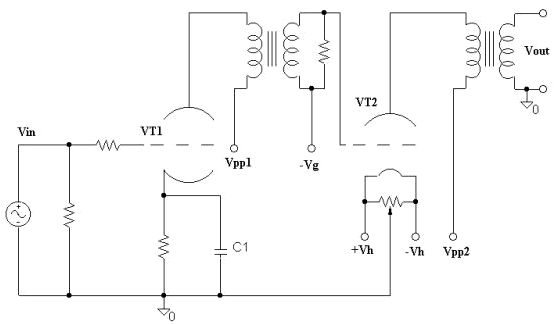
Fig. 6
 


are a “good” m and a low rp (that is an high gm) as well as a meaningful power dissipation. Canonical receiving tubes used in traditional amplifier design, like ECC83/12AX7, 6SN7 and so on,  can result unsatisfactory therefore I prefer vacuum tubes with best electrical performances like WE437A, 3A167M, E55L, E810F and others. Unfortunately the latters are rarer and expensive. Of course, you can resort to composite configurations like SRPP, MU-Follower’s, and Cascode+Cathode_Follower in order to exceed the inherent limitations of standard tubes. I stress the importance of a good driver because they result mandatory if you decide to design a class A2 amplifier or you take aim at exploring the enormous potentialities of direct heating big transmitting tubes like 211 and 845 that usually can present grid current already for weakly negative grid voltages. Further in this tubes the input capacities are not negligible and  a wide driving signal is requested.  

        From Fig.2, you have:

Ip1=g11*Vin1 + g12*Vin1^2                   (1);

Ip2=g21*Vin2 + g22*Vin2^2                   (2);

  where gij coefficients are costants inherent to the mutal dynamic charactersitcs of the two gain stages. You can extracts these coefficients with a mathematical or experimental method. Within the mathematical approach you can follow an analytical or numerical way. I prefer the latter because it connects speed and good precision without the idiosyncrasies of the simbolic calculus. For triodes, assuming that the effects  superior  to the second  order are negligible, and observing that:  

Vin2=-Z1*Ip1               (3);

Vout=-Z2*Ip2               (4);

 

by replacing the (1) and (2) in (3) and (4) rispectively it’s easy to reach at the following expression for the output voltage:

    Vout= g11*g21*Z1*Z2*Vin1+(g12*g21*Z1*Z2g11^2*g21*Z1^2)*Vin1^2+2*g11*g12*g22*Z1^2*Z2*Vin^3 (5)

 

where:

Vin1=Vp*sinwt            (6)

 

and therefore:

Vin1^2= 1/2*Vp^2*(1-cos2wt)      (7)

Vin1^3= 1/4*Vp^3*(3*sinwt-sin3wt)     (8)

 

(6) is the mathematical expression of the input signal while (7) and (8) are derived with a bit of  trigonometry.

    

By observing  (5)  two main considerations emerge:

· Also in the hypothesis of a 2nd order mutual dynamic characteristic for the common  cathode stages     the output signal present a 3rd order component;

· The algebraic expression between round brackets underlines the theoretical possibility for an  annulment   of the 2nd order component and thanks to (7) also for the rectified component; Unfortunately the exacts values for Z1 and Z2 that permits a reduction or nulling for the 2nd order effect  it’s hard to find since:  

    

(g11,g12)=f(Z1)            (9)

  (g21,g22)=f(Z2)          (10) 

   

(where d1, the “error” produced by the first triode, includes distortions, noise, hum, drift and so on);  next the criterion network b (that could also contain reactive element for frequency compensation)     attenuates the amplified signal  by the value 

  b = 1/G1             (11)

and finally:

Vin1= -G1*Vin + d1             (12)

Vout= -G2*{[(-G1Vin + d 1)*b] + d2}                 (13)

    where likewise the first stage G2 and d2 are the gain and the error for the second  one rispectively. By assuming:  

G1= G2= G= 1/b;            (14)

  eq. (13) is reduced to the following:

Vout= G * Vin  -  d 1  +  d2           (15)

and d1 and d2 are similar if:

 a)  both triodes are similar in their dynamic behaviour;

 b) the input signal swing it’s small;

 

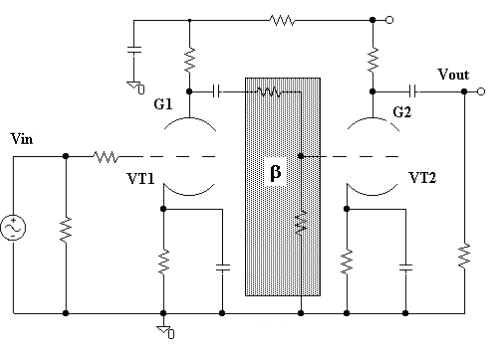
Fig. 7
 

therefore a lower value in the output signal THD  can result.
The reduction mechanism of even harmonics don’t have clearly the same effectiveness that you can  find         in ideal push-pull structures, where the input signals are really equal altough out-of-phase. In cascade stages as in Fig. 7 the 2nd stage receive and out-phase  signal with the “harmonic imprint”   caused from the 1st one. I have defined an Improvement Index (II):

                                                                                             

(16)

  
and its graphic shows good performances of the cascade  for small input signals, where the harmonic content in the 1st stage output  is not elevated, Fig. 8. For both tubes and bias points please refer to [2].

 

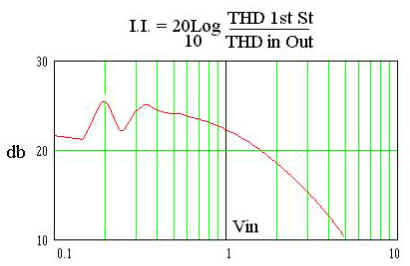
Fig. 8

         The mechanism that characterizes the behaviour of the circuit in Fig.7 could be used, duly adapted, for the realization of an electronic phase inverter for push-pull amplifiers and for a line stage with low THD, Fig. 9. A similar preamplifier presents a cumulative gain as the first stage, a low THD and, thanks to cathode-follower, a low output impedance.

Fig. 9


        Clearly,  other circumstances could require different bias points and/or vacuum tubes for the basic structure in Figs. 7,9. For this situations an “ad hoc” examen permits the best application of the HCT although the procedural mechanism is the same.  

References:

1 Radiotron Designer's Handbook RCA, pp. 509, 580-81, Chap XIV, 1953
2 RCA Receiving Tube Manual Technical Series RC-19, p. 344 1958

 

What did you think of this article?
Click here to send us your comments, feedback and suggestions