LA COPPIA E IL MOMENTO

    Esaminiamo il sistema di forze in fig. 1. Se proviamo a ricercare la risultante scopriremo che questa è nulla (3° Principio della Dinamica).

Fig. 1

   In realtà se applichiamo questo sistema di forze ad un corpo rigido come in fig. 2 ne avremo che a questo verrà impreso un moto rotatorio intorno ad un asse normale al piano di giacitura delle forze.

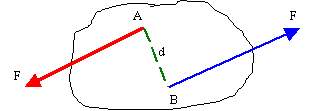
Fig. 2

   Questo tipo di sistema viene definito come coppia di forze. La distanza fra le due rette d'azione uguali e contrarie è detto braccio della coppia.

   Il prodotto dell'intensità della Forza F per il braccio d è una grandezza scalare definito come Momento di una Forza (Fig. 3):

Fig. 3

che tradotto in equazione

M = F x d (1)

    Consideriamo il sistema di forze riportato in fig. 4:

Fig. 4

   Proviamo ad individuare il Momento delle forze rappresentate:

M₁ = F₁ x (d₁+d₂+d₃+d₄)

M₂ = F₂ x (d₁+d₂+d₃)

M₃ = F₃ x (d₁+d₂)

M₄ = F₄ x d₄

che riportato in una unica equazione avrà come risultato

SM =  [F₁ x (d₁+d₂+d₃+d₄) + F₂ x (d₁+d₂+d₃) + F₃ x (d₁+d₂) + F₄ x d₄]   (2)

    Dalla cinematica sappiamo però che per un sistema di forze parallele e complanari è possibile determinare la propria Risulatante (Fig. 5) tramite l'applicazione del poligono funicolare.

Fig. 5

e quindi la (2) diverrà

M = R x D

questo risultato porta alla seguente considerazione

questa considerazione prende il nome di Teorema di varignon.