COMPOSIZIONE DELLE FORZE

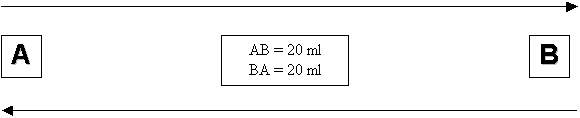
     Una vettura percorre 20 ml in linea retta, andando dal punto A al punto B per poi tornare in A, movendosi sempre in linea retta. Quale distanza ha percorso? Qual è stato il suo spostamento totale?

E’ chiaro che, la vettura ha percorso una distanza pari a

d = AB + BA = 20 + 20 = 40 ml

equivalente alla somma delle due “lunghezze”.

Ma attenzione, perché il suo SPOSTAMENTO complessivo è stato nullo, poiché è ritornata alla posizione iniziale, cioè, matematicamente:

Ds = AB + (-BA) = 20 + (-20) = 20 - 20 = 0 ml.

Questo “paradosso” si risolve ricordando che:

    - DISTANZA = grandezza scalare;

    - SPOSTAMENTO = grandezza vettoriale;

in definitiva mentre per sommare due (o più) DISTANZE occorre considerare soltanto i loro “moduli”, per sommare due spostamenti necessita tener conto anche della loro direzione e del loro verso.

    Vediamo adesso cosa succede nel caso in cui due forze non siano parallele, ma bensì complanari e concorrenti⁽¹⁾ con verso perpendicolare come in Fig. 1

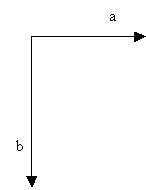
Fig. 1

   Ammettiamo che le forze indicate sopra abbiano la seguente intensità:

a = 10 Kg

b = 15 Kg.

quale sarà la sua somma? Viene spontaneo rispondere che

R = a + b = 10 + 15 = 25 Kg.

   E' questa la soluzione? Verifichiamo questa equazione sperimentalmente:

poniamo (in teoria) una barchetta nel letto di un canale e leghiamo alla sua prua (o prora) due corde statiche⁽²⁾ , una per lato del canale. Due persone prenderanno in mano l'estremità delle corde e con intensità pari a quella poc'anzi dichiarata cominceranno a tirare. Cosa succederà? la barchetta percorrerà una certa direzione con un verso preciso e la sua intensità?

   Analizziamo graficamente l'esperimento compiuto come in Fig. 2:

Fig. 2

quello che subito appare chiaro è che siamo in presenza di una terza forza che per convenzione chiameremo RISULTANTE (R).  Questa R non è altro che la somma tra i due vettori. Quindi si definisce somma fra vettori complanari concorrenti

    Analiticamente:

    1) applicazione del Teorema di Pitagora:

oppure

    2) applicazione regole della trigonometria piana⁽³⁾:

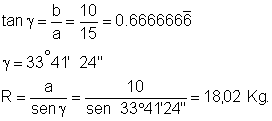
    Com'è evidente cambia il procedimento ma non il risultato.

   La soluzione grafica vista in precedenza viene definita REGOLA DEL PARALLELOGRAMMA. Un'altra soluzione grafica può essere trovata con l'applicazione della REGOLA DEL POLIGONO come mostrato in Fig. 3:

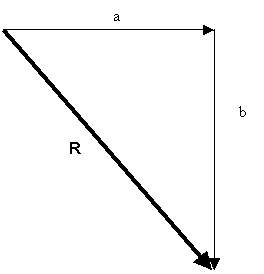
Fig. 3

    Anche in questo caso, cambia il metodo ma non il risultato.

Analizziamo altri casi.

1° CASO:

    Tre forze complanari concorrenti a, b e c.

    Nel caso in cui si verifichi il caso della Fig. 4

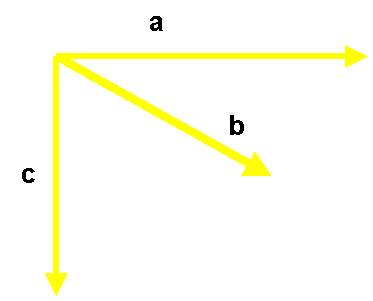
Fig. 4

   agiremo nel seguente modo:

a) si prendono in considerazione i vettori a e b e applicando una delle regole prima citate si ricava la loro Risultante; successivamente si considera il vettore R₁ appena trovato e il vettore c dei quali con le regole citate troviamo la Risultante R₂ . Il vettore trovato è la risultante di tutto il sistema di vettori considerato (vedi Fig. 5).  

Fig. 5

2° CASO:

    Tre vettori complanari non concorrenti a, b e c.

    Nel caso in cui si verifichi il caso della Fig. 5

  Fig. 6   

agiremo nel seguente modo:

a) si pongono i vettori a, b e c uno avanti l'altro facendo bene attenzione di non variare il verso; 

b) si congiunge la coda del vettore a con il vertice del vettore c;

c) il vettore trovato  R₁ è la risultante di tutto il sistema di vettori considerato (vedi Fig. 7).  

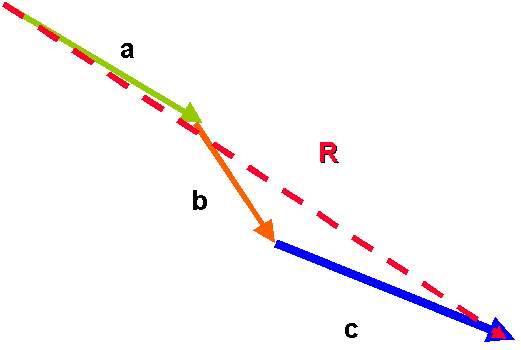
Fig. 7

3° CASO:

    Tre vettori complanari non concorrenti a, b e c parallele.

    Nel caso in cui si verifichi il caso della Fig. 8

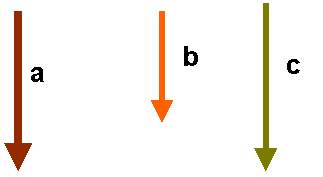
Fig. 8

agiremo nel seguente modo:

a) si pongono i vettori a, b e c uno avanti l'altro facendo bene attenzione di non variare il verso; 

b) si sceglie un punto o qualsiasi a lato si congiunge la coda del vettore a con il vertice del vettore c;

c) il vettore trovato  R₁ è la risultante di tutto il sistema di vettori considerato (vedi Fig. 7).  

Fig. 9

4° CASO:

    Tre vettori complanari non concorrenti a, b e c parallele.

    Nel caso in cui si verifichi il caso della Fig. 10

Fig. 10

agiremo come nel 3° caso presentato (vedi Fig. 11).

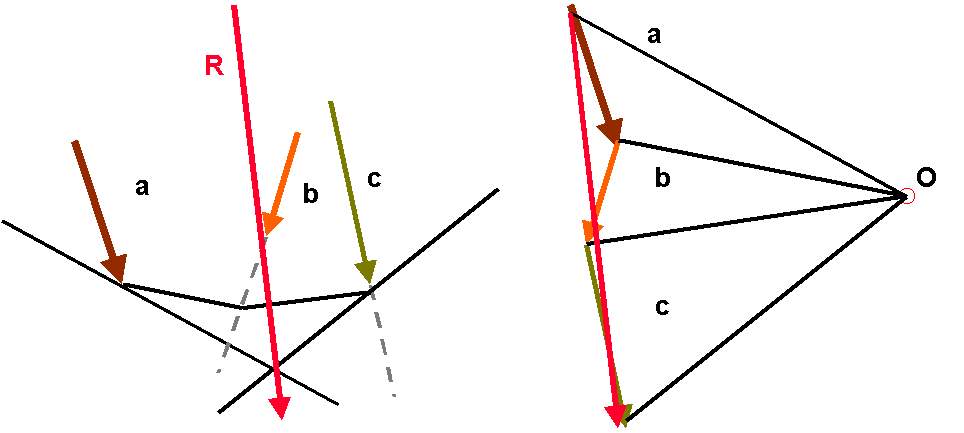
Fig. 11