Nella sezione dedicata alla caduta dei gravi abbiamo stabilito, con sistema galileano, che la sua legge può scriversi:

(1)

adesso verifichiamo questa ipotesi attraverso una serie di equazioni denominate EQUAZIONI CINEMATICHE.

    Dall'equazione

(2)

si ricavano la velocità  V e il tempo t:

(3)  (Equazione Cinematica 1)

(4)

    Visto che a è costante deduciamo che

    Nel grafico disegnato nella fig. 1 la (3)  è rappresentata per V₀ = 0 m/s²  con i tempi sull'asse delle ascisse (x) e la Velocità sulle ordinate (y).  Le due semirette corrispondono a valori diversi  dell'accelerazione. E' subito evidente che all'aumentare dell'accelerazione aumenta la pendenza.

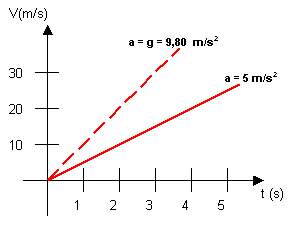
Fig. 1

    Nel grafico disegnato nella fig. 2  la (3)  è rappresentata per V₀ = 10 m/s² con i tempi sull'asse delle ascisse (x) e la Velocità sulle ordinate (y).  Le due semirette sono parallele alle precedenti anche se l'origine è cambiata. Anche in questo caso è evidente che all'aumentare dell'accelerazione aumenta la pendenza.

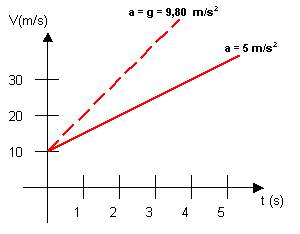
Fig. 2

 Calcoliamo la Velocità media per definizione:

(5)

Velocità calcolata con la media aritmetica:

(6)

risolvendo l’uguaglianza (5)=(6)

(7)

avremo l’equazione cinematica (2):

(8)

 sostituendo poi la (3) nella (8) avremo l’equazione cinematica (3):

(9)

(10)

(11)

(12)

infine, sostituendo la (4) nella (8) avremo:

(13)

(14)

(15)

(16)

fino a d arrivare alla  equazione cinematica 4:

 In caso di un corpo in caduta libera: a = -g

Per trovare la max altezza di un corpo lanciato in aria: usare la (12) con v₀ = 0 e a=-g