
![]()
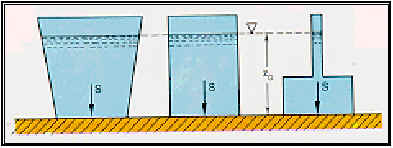
Fig. 1
Per la LEGGE DI STEVINO la pressione sul fondo dei tre recipienti in Fig. 1, aventi superfici di base A uguale, non cambia
Quindi la pressione unitaria p =
g h non cambia. Questo non si può dire però del peso che varia perché ogni contenitore, presentando forma diversa, contiene una massa di liquido differente (P=m g).
Esaminiamo ora due cilindri colmi di liquido, comunicanti fra loro come in fig.2
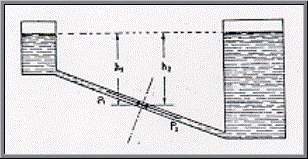
Fig. 2
Consideriamo una sezione "x" nel tubo di raccordo: se p1 > p2 avremo un repentino svuotamento del recipiente più piccolo ai danni dell’altro, viceversa se p1 < p2.
E’ chiaro quindi che per la LEGGE DI STEVINO avremo che
p1 = p2 => h1
g = h2 gQuesto equilibrio determina il piano "orizzontale" fra i due recipienti comunicanti ed è detto PRINCIPIO DEI VASI COMUNICANTI (fatta eccezione per quanto enunciato dalla legge JURIN-BORELLI sui vasi capillari che vedremo in seguito).