Dalla meccanica elementare sappiamo che un elemento di massa fluida in movimento appartenente ad una Sezione S, possiede una certa dose di energia dovuta (fig. 1):
Fig. 1
Quindi Bernulli enuncia che: in qualunque sezione di una vena liquida (ideale) in regime di moto permanente (o uniforme) la somma dell’energia potenziale (Ep), cinetica (Ec) e piezometrica (Eh) è costante, cioè non varia da sezione a sezione.
Ep + Ec + Eh = cost.
Ep = p h; Ec = ![]() ; Eh =
; Eh = ![]()
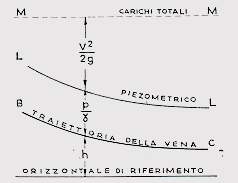
Fig. 2
Analizziamo i tre termini facendo riferimento ad una massa unitaria di liquido:
| ENERGIA POTENZIALE (Ep): |
è l’energia dipendente dalla quota (h) altimetrica alla quale è posta la massa liquida. |
|
Ep = Forza x spostamento |
Dove: F = P (peso della massa unitaria);
s = h (quota altimetrica della massa unitaria)
quindi
Ep = P h
| ENERGIA CINETICA (Ec): | è l’energia dipendente dalla velocità (V) che possiede la massa unitaria sottoposta ad un MOTO NATURALMENTE ACCELLERATO in conseguenza del campo gravitazionale in cui è immersa. |
|
Ec = Forza x spostamento |
Dove:
F = massa x aaccellerazione
Quindi:
![]()
dove
![]() (moto uniformemente
accelerato)
(moto uniformemente
accelerato)
sostituendo avremo:
![]()
Ma se V = at allora V2 = a2t2 quindi:
![]()
Dalla fisica sappiamo che il peso "P" equivale alla massa "m" per l’accelerazione di gravità "g", quindi tradotto in formula:
![]()
di conseguenza
![]()
sostituendo alla (1) otterremo:
![]()
| ENERGIA PIEZOMETRICA (Eh): | è l’energia dipendente dalla pressione idrostatica "p" esistente sulla massa unitaria in movimento con velocità "V" |
Eh = Forza x spostament |
Dove:
F = p A (spinta idrostatica sulla sezione A)
S = V t (spostamento nel tempo unitario)
Quindi sostituendo:
Eh = p A V t
Ma sappiamo che V A = Q e quindi sostituendo avremo
Eh = p t Q
Sapendo che il peso "P" è uguale al prodotto della portata "Q" per il peso specifico"g" nell’unità di tempo "t" considerato
P = Q g t
e di conseguenza
![]()
avremo così
![]()
Quindi l’equazione di Bernulli Ep + Ec + Eh = cost. diverrà:
![]()
e dividendo il tutto per il peso "P" avremo:
![]()
Applicando questo principio per due sezioni distinte avremo:
![]()
Si noti che tutti i termini dell’equazione possono essere interpretati come altezze o quote altimetriche:
- ![]() quota altimetrica dell’asse della corrente nella sezione in esame;
quota altimetrica dell’asse della corrente nella sezione in esame;
-
![]() altezza di caduta occorrente ad un grave di massa unitaria, sottoposto all’accelerazione "g", per raggiungere la velocità "V";
altezza di caduta occorrente ad un grave di massa unitaria, sottoposto all’accelerazione "g", per raggiungere la velocità "V";
-
![]() quota, rispetto all’asse della corrente, cui corrisponderebbe il liquido se inserissimo sulla sezione considerata un tubo
manometrico.
quota, rispetto all’asse della corrente, cui corrisponderebbe il liquido se inserissimo sulla sezione considerata un tubo
manometrico.